"Το πρώτο μέρος καθορίζει τις διατάξεις που είναι ελάχιστα απαραίτητες για την κατανόηση των χημειομετρικών και το δεύτερο μέρος περιέχει τα στοιχεία που πρέπει να γνωρίζετε για μια βαθύτερη κατανόηση των μεθόδων πολυμεταβλητής ανάλυσης. Η παρουσίαση απεικονίζεται με παραδείγματα που έγιναν στο βιβλίο εργασίας του Excel Matrix.xls, που συνοδεύει το παρόν έγγραφο.

Οι σύνδεσμοι σε παραδείγματα τοποθετούνται στο κείμενο ως αντικείμενα του Excel. Αυτά τα παραδείγματα είναι αφηρημένης φύσης· σε καμία περίπτωση δεν συνδέονται με τα προβλήματα της αναλυτικής χημείας. Παραδείγματα της πραγματικής ζωής της χρήσης της άλγεβρας μήτρας στη χημειομετρία συζητούνται σε άλλα κείμενα που καλύπτουν μια ποικιλία χημειομετρικών εφαρμογών.

Οι περισσότερες μετρήσεις που γίνονται στην αναλυτική χημεία δεν είναι άμεσες, αλλά έμμεσος. Αυτό σημαίνει ότι στο πείραμα, αντί για την τιμή της επιθυμητής αναλυόμενης ουσίας C (συγκέντρωση), προκύπτει μια άλλη τιμή Χ(σήμα), σχετικό αλλά όχι ίσο με το C, δηλ. Χ(Γ) ≠ Γ. Κατά κανόνα το είδος της εξάρτησης ΧΤο (C) είναι άγνωστο, αλλά ευτυχώς στην αναλυτική χημεία οι περισσότερες μετρήσεις είναι αναλογικές. Αυτό σημαίνει ότι με την αύξηση της συγκέντρωσης του C σε έναφορές, το σήμα Χ θα αυξηθεί κατά το ίδιο ποσό, δηλ. Χ(έναΓ) = ένα x(ΝΤΟ). Επιπλέον, τα σήματα είναι επίσης προσθετικά, επομένως το σήμα από ένα δείγμα στο οποίο υπάρχουν δύο ουσίες με συγκεντρώσεις C 1 και C 2 θα είναι ίσο με το άθροισμα των σημάτων από κάθε συστατικό, δηλ. Χ(C 1 + C 2) = Χ(C 1)+ Χ(Γ 2). Η αναλογικότητα και η προσθετικότητα μαζί δίνουν γραμμικότητα. Πολλά παραδείγματα μπορούν να δοθούν για να διευκρινιστεί η αρχή της γραμμικότητας, αλλά αρκεί να αναφέρουμε τα δύο πιο εντυπωσιακά παραδείγματα - τη χρωματογραφία και τη φασματοσκοπία. Το δεύτερο χαρακτηριστικό που είναι εγγενές σε ένα πείραμα στην αναλυτική χημεία είναι πολυκαναλικό. Ο σύγχρονος αναλυτικός εξοπλισμός μετρά ταυτόχρονα τα σήματα για πολλά κανάλια. Για παράδειγμα, η ένταση της μετάδοσης του φωτός μετράται για πολλά μήκη κύματος ταυτόχρονα, δηλ. εύρος. Επομένως, στο πείραμα έχουμε να κάνουμε με πολλά σήματα Χ 1 , Χ 2 ,...., Χ n, που χαρακτηρίζει το σύνολο των συγκεντρώσεων C 1 , C 2 , ..., C m των ουσιών που υπάρχουν στο υπό μελέτη σύστημα.

Ρύζι. 1 Φάσματα

Έτσι, ένα αναλυτικό πείραμα χαρακτηρίζεται από γραμμικότητα και πολυδιάσταση. Επομένως, είναι βολικό να θεωρούνται τα πειραματικά δεδομένα ως διανύσματα και πίνακες και να τα χειρίζονται χρησιμοποιώντας τη συσκευή της άλγεβρας πινάκων. Η καρποφορία αυτής της προσέγγισης φαίνεται από το παράδειγμα που παρουσιάζεται, το οποίο παρουσιάζει τρία φάσματα που λαμβάνονται σε 200 μήκη κύματος από 4000 έως 4796 cm −1. Το πρώτο (x 1) και το δεύτερο (x 2) φάσματα ελήφθησαν για τυπικά δείγματα στα οποία είναι γνωστές οι συγκεντρώσεις δύο ουσιών Α και Β: στο πρώτο δείγμα [A] = 0,5, [B] = 0,1 και στο δεύτερο δείγμα [A] = 0,2, [B] = 0,6. Τι μπορεί να ειπωθεί για ένα νέο, άγνωστο δείγμα, το φάσμα του οποίου ορίζεται x 3;

Ας θεωρήσουμε τρία πειραματικά φάσματα x 1, x 2 και x 3 ως τρία διανύσματα διάστασης 200. Χρησιμοποιώντας τη γραμμική άλγεβρα, μπορούμε εύκολα να δείξουμε ότι x 3 = 0,1 x 1 +0,3 x 2, επομένως, στο τρίτο δείγμα, μόνο οι ουσίες Α και Β υπάρχουν προφανώς σε συγκεντρώσεις [A] = 0,5×0,1 + 0,2×0,3 = 0,11 και [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Βασικές πληροφορίες 1.1 Πίνακες

Μήτραονομάζεται ένας ορθογώνιος πίνακας αριθμών, για παράδειγμα

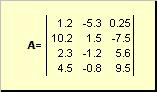
Ρύζι. 2 Matrix

Οι πίνακες συμβολίζονται με κεφαλαία έντονα γράμματα (Α) και τα στοιχεία τους με αντίστοιχα πεζά γράμματα με δείκτες, δηλ. ένα ij. Το πρώτο ευρετήριο αριθμεί τις σειρές και το δεύτερο - τις στήλες. Στη χημειομετρία, συνηθίζεται να δηλώνεται η μέγιστη τιμή ενός δείκτη με το ίδιο γράμμα με τον ίδιο τον δείκτη, αλλά με κεφαλαία γράμματα. Επομένως, ο πίνακας Α μπορεί επίσης να γραφτεί ως ( ένα ij , Εγώ = 1,..., Εγώ; ι = 1,..., J). Για το παράδειγμα πίνακα Εγώ = 4, J= 3 και ένα 23 = −7.5.

Ζεύγος αριθμών ΕγώΚαι Jονομάζεται διάσταση του πίνακα και συμβολίζεται ως Εγώ× J. Ένα παράδειγμα μήτρας στη χημειομετρία είναι ένα σύνολο φασμάτων που λαμβάνεται για Εγώδείγματα για Jμήκη κύματος.

1.2. Οι απλούστερες πράξεις με πίνακες

Οι μήτρες μπορούν να είναι πολλαπλασιάστε με αριθμούς. Σε αυτήν την περίπτωση, κάθε στοιχείο πολλαπλασιάζεται με αυτόν τον αριθμό. Για παράδειγμα -

Ρύζι. 3 Πολλαπλασιάζοντας έναν πίνακα με έναν αριθμό

Δύο πίνακες της ίδιας διάστασης μπορούν να είναι στοιχείο προς στοιχείο πτυχήΚαι αφαιρώ. Για παράδειγμα,

Ρύζι. 4 Προσθήκη μήτρας

Ως αποτέλεσμα του πολλαπλασιασμού με έναν αριθμό και της πρόσθεσης, προκύπτει ένας πίνακας της ίδιας διάστασης.

Ο μηδενικός πίνακας είναι ένας πίνακας που αποτελείται από μηδενικά. Συμβολίζεται Ο. Προφανώς, A +O = A, A −A = O και 0A = O.

Η μήτρα μπορεί να είναι μεταθέτω. Κατά τη διάρκεια αυτής της λειτουργίας, η μήτρα αναστρέφεται, δηλ. οι γραμμές και οι στήλες ανταλλάσσονται. Η μεταφορά υποδεικνύεται με έναν πρώτο, A" ή δείκτη A t. Έτσι, εάν A = ( ένα ij , Εγώ = 1,..., Εγώ; ι = 1,...,J), τότε A t = ( ένα ji , ι = 1,...,J; i = 1,..., Εγώ). Για παράδειγμα

Ρύζι. 5 Μεταφορά μήτρας

Είναι προφανές ότι (A t) t = A, (A + B) t = A t + B t.

1.3. Πολλαπλασιασμός πίνακα

Οι μήτρες μπορούν να είναι πολλαπλασιάζω, αλλά μόνο εάν έχουν τις κατάλληλες διαστάσεις. Το γιατί συμβαίνει αυτό θα γίνει σαφές από τον ορισμό. Προϊόν του πίνακα Α, διάσταση Εγώ× κ, και πίνακας Β, διάσταση κ× J, που ονομάζεται πίνακας C, διάσταση Εγώ× J, του οποίου τα στοιχεία είναι αριθμοί

Έτσι, για το γινόμενο ΑΒ είναι απαραίτητο ο αριθμός των στηλών στον αριστερό πίνακα Α να είναι ίσος με τον αριθμό των σειρών στον δεξιό πίνακα Β. Ένα παράδειγμα προϊόντος μήτρας -

Εικ.6 Προϊόν πινάκων

Ο κανόνας για τον πολλαπλασιασμό του πίνακα μπορεί να διατυπωθεί ως εξής. Για να βρεθεί ένα στοιχείο του πίνακα C στη διασταύρωση Εγώ-η γραμμή και ιη στήλη ( ντο ij) πρέπει να πολλαπλασιαστεί στοιχείο προς στοιχείο Εγώ-η σειρά του πρώτου πίνακα A on ιη στήλη του δεύτερου πίνακα Β και προσθέστε όλα τα αποτελέσματα. Έτσι, στο παράδειγμα που φαίνεται, ένα στοιχείο από την τρίτη σειρά και τη δεύτερη στήλη λαμβάνεται ως το άθροισμα των προϊόντων της τρίτης σειράς Α και της δεύτερης στήλης Β.

Εικ.7 Στοιχείο του γινομένου πινάκων

Το γινόμενο των πινάκων εξαρτάται από τη σειρά, δηλ. AB ≠ BA, τουλάχιστον για λόγους διαστάσεων. Λένε ότι είναι μη ανταλλακτική. Ωστόσο, το γινόμενο των πινάκων είναι συνειρμικό. Αυτό σημαίνει ότι ABC = (AB)C = A(BC). Επιπλέον, είναι και διανεμητικό, δηλ. A (B +C) = AB +AC. Προφανώς ΑΟ = Ο.

1.4. Τετράγωνες μήτρες

Εάν ο αριθμός των στηλών του πίνακα είναι ίσος με τον αριθμό των σειρών του ( Εγώ = J=N), τότε ένας τέτοιος πίνακας ονομάζεται τετράγωνο. Σε αυτή την ενότητα θα εξετάσουμε μόνο τέτοιους πίνακες. Μεταξύ αυτών των πινάκων διακρίνονται πίνακες με ειδικές ιδιότητες.

Μονόκλινομήτρας (συμβολίζεται I, και μερικές φορές E) είναι ένας πίνακας στον οποίο όλα τα στοιχεία είναι ίσα με μηδέν, με εξαίρεση τα διαγώνια, τα οποία είναι ίσα με 1, δηλ.

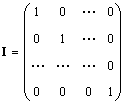
Προφανώς AI = IA = A.

Ο πίνακας ονομάζεται διαγώνιος, εάν όλα τα στοιχεία του εκτός από τα διαγώνια ( ένα ii) ισούνται με μηδέν. Για παράδειγμα

Ρύζι. 8 Διαγώνιος πίνακας

Ο πίνακας Α ονομάζεται ανώτερος τριγωνικός, αν όλα τα στοιχεία του που βρίσκονται κάτω από τη διαγώνιο είναι ίσα με μηδέν, δηλ. ένα ij= 0, στο Εγώ>ι. Για παράδειγμα

Ρύζι. 9 Ανώτερος τριγωνικός πίνακας

Η κάτω τριγωνική μήτρα ορίζεται παρόμοια.

Ο πίνακας Α ονομάζεται συμμετρικός, αν A t = A . Με άλλα λόγια ένα ij = ένα ji. Για παράδειγμα

Ρύζι. 10 Συμμετρικός πίνακας

Ο πίνακας Α ονομάζεται ορθογώνιο, Αν

A t A = AA t = I .

Ο πίνακας ονομάζεται κανονικόςΑν

1.5. Ίχνη και καθοριστική

ΕπόμενοΟ τετραγωνικός πίνακας A (που συμβολίζεται με Tr(A) ή Sp(A)) είναι το άθροισμα των διαγώνιων στοιχείων του,

Για παράδειγμα,

Ρύζι. 11 Ίχνη μήτρας

Είναι προφανές ότι

Sp(α A ) = α Sp(A ) και

Sp(A +B) = Sp(A)+ Sp(B).

Μπορεί να αποδειχθεί ότι

Sp(A) = Sp(A t), Sp(I) = Ν,

και επίσης αυτό

Sp(AB) = Sp(BA).

Ένα άλλο σημαντικό χαρακτηριστικό ενός τετραγωνικού πίνακα είναι το δικό του καθοριστικός(σημειώνεται det(A )). Ορισμός ορίζουσας σε γενική περίπτωσηαρκετά περίπλοκο, οπότε θα ξεκινήσουμε με την απλούστερη επιλογή - έναν πίνακα Α με διάσταση (2x2). Επειτα

Για έναν πίνακα (3×3) η ορίζουσα θα είναι ίση με

Στην περίπτωση του πίνακα ( Ν× Ν) η ορίζουσα υπολογίζεται ως το άθροισμα 1·2·3· ... · Ν= Ν! όρους, καθένας από τους οποίους είναι ίσος

Ευρετήρια κ 1 , κ 2 ,..., κ Νορίζονται ως όλες οι πιθανές διατεταγμένες μεταθέσεις rαριθμοί στο σετ (1, 2, ..., Ν). Ο υπολογισμός της ορίζουσας ενός πίνακα είναι μια πολύπλοκη διαδικασία, η οποία στην πράξη πραγματοποιείται με τη χρήση ειδικών προγραμμάτων. Για παράδειγμα,

Ρύζι. 12 Ορίζουσα μήτρας

Ας σημειώσουμε μόνο τις προφανείς ιδιότητες:

det(I ) = 1, det(A ) = det(A t),

det(AB) = det(A)det(B).

1.6. Διανύσματα

Εάν ο πίνακας αποτελείται από μία μόνο στήλη ( J= 1), τότε καλείται ένα τέτοιο αντικείμενο διάνυσμα. Πιο συγκεκριμένα, διάνυσμα στήλης. Για παράδειγμα

Μπορεί κανείς επίσης να εξετάσει πίνακες που αποτελούνται από μία γραμμή, για παράδειγμα

Αυτό το αντικείμενο είναι επίσης ένα διάνυσμα, αλλά διάνυσμα σειράς. Κατά την ανάλυση δεδομένων, είναι σημαντικό να κατανοήσουμε με ποια διανύσματα έχουμε να κάνουμε - στήλες ή γραμμές. Έτσι, το φάσμα που λαμβάνεται για ένα δείγμα μπορεί να θεωρηθεί ως διάνυσμα γραμμής. Στη συνέχεια, το σύνολο των φασματικών εντάσεων σε ένα ορισμένο μήκος κύματος για όλα τα δείγματα θα πρέπει να αντιμετωπίζεται ως διάνυσμα στήλης.

Η διάσταση ενός διανύσματος είναι ο αριθμός των στοιχείων του.

Είναι σαφές ότι οποιοδήποτε διάνυσμα στήλης μπορεί να μετατραπεί σε διάνυσμα γραμμής με μεταφορά, δηλ.

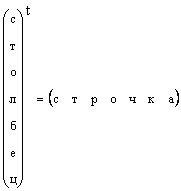
Σε περιπτώσεις όπου το σχήμα του διανύσματος δεν προσδιορίζεται συγκεκριμένα, αλλά λέγεται απλώς ότι είναι διάνυσμα, τότε σημαίνουν διάνυσμα στήλης. Θα τηρήσουμε επίσης αυτόν τον κανόνα. Ένα διάνυσμα συμβολίζεται με ένα πεζό, όρθιο, έντονο γράμμα. Ένα μηδενικό διάνυσμα είναι ένα διάνυσμα του οποίου όλα τα στοιχεία είναι μηδέν. Ονομάζεται 0.

1.7. Οι απλούστερες πράξεις με διανύσματα

Τα διανύσματα μπορούν να προστεθούν και να πολλαπλασιαστούν με αριθμούς με τον ίδιο τρόπο όπως οι πίνακες. Για παράδειγμα,

Ρύζι. 13 Πράξεις με διανύσματα

Καλούνται δύο διανύσματα x και y γραμμική, αν υπάρχει αριθμός α τέτοιος ώστε

1.8. Προϊόντα διανυσμάτων

Δύο διανύσματα ίδιας διάστασης Νμπορεί να πολλαπλασιαστεί. Έστω δύο διανύσματα x = ( Χ 1 , Χ 2 ,...,Χ N) t και y = ( y 1 , y 2 ,...,yΝ) t . Με οδηγό τον κανόνα πολλαπλασιασμού γραμμή προς στήλη, μπορούμε να συνθέσουμε δύο γινόμενα από αυτά: x t y και xy t. Πρώτη δουλειά

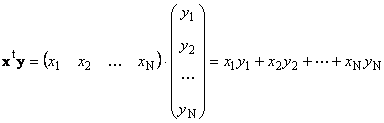
που ονομάζεται βαθμωτό μέγεθοςή εσωτερικός. Το αποτέλεσμα του είναι ένας αριθμός. Ο συμβολισμός (x ,y )= x t y χρησιμοποιείται επίσης για αυτό. Για παράδειγμα,

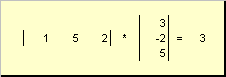
Ρύζι. 14 Εσωτερικό (βαθμωτό) προϊόν

Δεύτερο κομμάτι

που ονομάζεται εξωτερικός. Το αποτέλεσμα είναι ένας πίνακας διαστάσεων ( Ν× Ν). Για παράδειγμα,

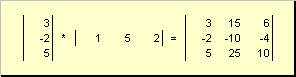
Ρύζι. 15 Εξωτερική εργασία

Διανύσματα, κλιμακωτό προϊόνπου ισούται με μηδέν λέγονται ορθογώνιο.

1.9. Διάνυσμα κανόνα

Το κλιμακωτό γινόμενο ενός διανύσματος με τον εαυτό του ονομάζεται βαθμωτό τετράγωνο. Αυτή η τιμή

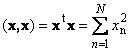
ορίζει ένα τετράγωνο μήκοςδιάνυσμα x. Για να υποδείξετε μήκος (ονομάζεται επίσης ο κανόναςδιάνυσμα) χρησιμοποιείται ο συμβολισμός

Για παράδειγμα,

Ρύζι. 16 Διανυσματικός κανόνας

Ένα διάνυσμα μοναδιαίου μήκους (||x || = 1) ονομάζεται κανονικοποιημένο. Ένα μη μηδενικό διάνυσμα (x ≠ 0) μπορεί να κανονικοποιηθεί διαιρώντας το με το μήκος του, δηλ. x = ||x || (x/ ||x ||) = ||x || μι. Εδώ e = x/ ||x || - κανονικοποιημένο διάνυσμα.

Τα διανύσματα ονομάζονται ορθοκανονικά εάν είναι όλα κανονικοποιημένα και κατά ζεύγη ορθογώνια.

1.10. Γωνία μεταξύ των διανυσμάτων

Το κλιμακωτό γινόμενο καθορίζει και γωνίαφ μεταξύ δύο διανυσμάτων x και y

Αν τα διανύσματα είναι ορθογώνια, τότε cosφ = 0 και φ = π/2, και αν είναι συγγραμμικά, τότε cosφ = 1 και φ = 0.

1.11. Διανυσματική αναπαράσταση ενός πίνακα

Κάθε πίνακας Α μεγέθους Εγώ× Jμπορεί να αναπαρασταθεί ως ένα σύνολο διανυσμάτων

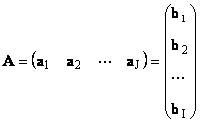
Εδώ κάθε διάνυσμα α ιείναι ιη στήλη και το διάνυσμα γραμμής β Εγώείναι Εγώη σειρά του πίνακα Α

1.12. Γραμμικά εξαρτώμενα διανύσματα

Διανύσματα ίδιας διάστασης ( Ν) μπορεί να προστεθεί και να πολλαπλασιαστεί με έναν αριθμό, όπως και οι πίνακες. Το αποτέλεσμα θα είναι ένα διάνυσμα της ίδιας διάστασης. Έστω πολλά διανύσματα της ίδιας διάστασης x 1, x 2,...,x K και ο ίδιος αριθμός αριθμών α α 1, α 2,...,α κ. Διάνυσμα

y = α 1 x 1 + α 2 x 2 +...+ α κΧ κ

που ονομάζεται γραμμικός συνδυασμόςδιανύσματα x κ .

Αν υπάρχουν τέτοιοι μη μηδενικοί αριθμοί α κ ≠ 0, κ = 1,..., κότι y = 0, τότε ένα τέτοιο σύνολο διανυσμάτων x κπου ονομάζεται γραμμικά εξαρτώμενη. Διαφορετικά, τα διανύσματα λέγονται ότι είναι γραμμικά ανεξάρτητα. Για παράδειγμα, τα διανύσματα x 1 = (2, 2) t και x 2 = (−1, −1) t εξαρτώνται γραμμικά, επειδή x 1 +2x 2 = 0

1.13. Κατάταξη μήτρας

Σκεφτείτε ένα σύνολο από κδιανύσματα x 1 , x 2 ,...,x κδιαστάσεις Ν. Η κατάταξη αυτού του συστήματος διανυσμάτων είναι ο μέγιστος αριθμός γραμμικά ανεξάρτητων διανυσμάτων. Για παράδειγμα στο σετ

υπάρχουν μόνο δύο γραμμικά ανεξάρτητα διανύσματα, για παράδειγμα x 1 και x 2, οπότε η κατάταξή του είναι 2.

Προφανώς, εάν υπάρχουν περισσότερα διανύσματα σε ένα σύνολο από τη διάστασή τους ( κ>Ν), τότε είναι απαραίτητα γραμμικά εξαρτημένα.

Κατάταξη μήτρας(συμβολίζεται με κατάταξη (Α)) είναι η κατάταξη του συστήματος των διανυσμάτων από το οποίο αποτελείται. Αν και οποιοσδήποτε πίνακας μπορεί να αναπαρασταθεί με δύο τρόπους (διανύσματα στήλης ή γραμμής), αυτό δεν επηρεάζει την τιμή κατάταξης, επειδή

1.14. αντίστροφη μήτρα

Ένας τετράγωνος πίνακας Α ονομάζεται μη ενικός εάν έχει μοναδικό ΑΝΤΙΣΤΡΟΦΗμήτρα Α -1 που καθορίζεται από τις συνθήκες

AA −1 = A −1 A = I .

Ο αντίστροφος πίνακας δεν υπάρχει για όλους τους πίνακες. Απαραίτητη και επαρκής προϋπόθεση για τον μη εκφυλισμό είναι

det(A) ≠ 0 ή κατάταξη(A) = Ν.

Η αντιστροφή μήτρας είναι μια πολύπλοκη διαδικασία για την οποία υπάρχουν ειδικά προγράμματα. Για παράδειγμα,

Ρύζι. 17 Αντιστροφή πίνακα

Ας παρουσιάσουμε τους τύπους για την απλούστερη περίπτωση - έναν πίνακα 2×2

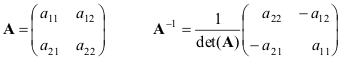
Αν οι πίνακες Α και Β δεν είναι μοναδικοί, τότε

(AB ) −1 = B −1 A −1 .

1.15. Ψευδής αντίστροφη μήτρα

Εάν ο πίνακας Α είναι ενικός και ο αντίστροφος πίνακας δεν υπάρχει, τότε σε ορισμένες περιπτώσεις μπορείτε να χρησιμοποιήσετε ψευδοαντίστροφομήτρας, ο οποίος ορίζεται ως πίνακας Α+ τέτοιος ώστε

ΑΑ + Α = Α.

Η ψευδοανάστροφη μήτρα δεν είναι η μόνη και η μορφή της εξαρτάται από τη μέθοδο κατασκευής. Για παράδειγμα, για μια ορθογώνια μήτρα μπορείτε να χρησιμοποιήσετε τη μέθοδο Moore-Penrose.

Αν ο αριθμός των στηλών μικρότερος αριθμόςγραμμές, λοιπόν

A + =(A t A ) −1 A t

Για παράδειγμα,

Ρύζι. 17α Ψευδοαναστροφή μήτρας

Αν ο αριθμός των στηλών περισσότερος αριθμόςγραμμές, λοιπόν

A + =A t (AA t) −1

1.16. Πολλαπλασιάζοντας ένα διάνυσμα με έναν πίνακα

Το διάνυσμα x μπορεί να πολλαπλασιαστεί με έναν πίνακα Α κατάλληλης διάστασης. Σε αυτήν την περίπτωση, το διάνυσμα στήλης πολλαπλασιάζεται στο δεξιό Ax και το διάνυσμα γραμμής πολλαπλασιάζεται στο αριστερό x t A. Αν η διανυσματική διάσταση Jκαι τη διάσταση του πίνακα Εγώ× Jτότε το αποτέλεσμα θα είναι ένα διάνυσμα διάστασης Εγώ. Για παράδειγμα,

Ρύζι. 18 Πολλαπλασιάζοντας ένα διάνυσμα με έναν πίνακα

Αν ο πίνακας Α είναι τετράγωνος ( Εγώ× Εγώ), τότε το διάνυσμα y = Ax έχει την ίδια διάσταση με το x. Είναι προφανές ότι

A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Επομένως, οι πίνακες μπορούν να θεωρηθούν ως γραμμικοί μετασχηματισμοί διανυσμάτων. Συγκεκριμένα, Ix = x, Ox = 0.

2. Πρόσθετες πληροφορίες 2.1. Συστήματα γραμμικές εξισώσεις

Έστω Α ένας πίνακας μεγέθους Εγώ× J, και b είναι το διάνυσμα διάστασης J. Θεωρήστε την εξίσωση

Τσεκούρι = β

σε σχέση με το διάνυσμα x, διάσταση Εγώ. Ουσιαστικά, είναι ένα σύστημα Εγώγραμμικές εξισώσεις με Jάγνωστος Χ 1 ,...,Χ J. Λύση υπάρχει αν και μόνο αν

rank(A) = rank(B) = R,

όπου Β είναι ο πίνακας επαυξημένης διάστασης Εγώ×( J+1), που αποτελείται από έναν πίνακα A που συμπληρώνεται από μια στήλη b, B = (A b). Διαφορετικά, οι εξισώσεις είναι ασυνεπείς.

Αν R = Εγώ = J, τότε η λύση είναι μοναδική

x = A −1 b .

Αν R < Εγώ, τότε είναι πολλά διάφορες λύσεις, που μπορεί να εκφραστεί μέσω ενός γραμμικού συνδυασμού J−Rφορείς. Σύστημα ομοιογενείς εξισώσεις Ax = 0 με τετράγωνο πίνακα A ( Ν× Ν) έχει μια μη τετριμμένη λύση (x ≠ 0) αν και μόνο αν det(A) = 0. Αν R= κατάταξη (Α) 0.

Ομοίως ορίζεται αρνητικός(x t Αξ< 0), μη αρνητικό(x t Ax ≥ 0) και αρνητικός(x t Ax ≤ 0) ορισμένοι πίνακες.

2.4. Αποσύνθεση Cholesky

Εάν ένας συμμετρικός πίνακας Α είναι θετικός ορισμένος, τότε υπάρχει ένας μοναδικός τριγωνικός πίνακας U με θετικά στοιχεία για τον οποίο

A = U t U .

Για παράδειγμα,

Ρύζι. 19 Αποσύνθεση Cholesky

2.5. Πολική αποσύνθεση

Έστω το Α μη εκφυλισμένο τετράγωνη μήτραδιαστάσεις Ν× Ν. Στη συνέχεια, υπάρχει ένα μοναδικό πολικόςεκτέλεση

A = SR,

όπου το S είναι ένας μη αρνητικός συμμετρικός πίνακας και το R είναι ένας ορθογώνιος πίνακας. Οι πίνακες S και R μπορούν να οριστούν ρητά:

S 2 = AA t ή S = (AA t) ½ και R = S −1 A = (AA t) −½ A .

Για παράδειγμα,

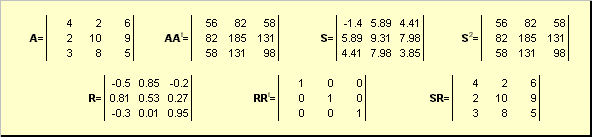
Ρύζι. 20 Πολική αποσύνθεση

Εάν ο πίνακας A είναι ενικός, τότε η αποσύνθεση δεν είναι μοναδική - δηλαδή: το S είναι ακόμα ένα, αλλά μπορεί να υπάρχουν πολλά R. Η πολική αποσύνθεση αντιπροσωπεύει τη μήτρα Α ως συνδυασμό συμπίεσης/επέκτασης S και περιστροφής R .

2.6. Ιδιοδιανύσματα και ιδιοτιμές

Έστω το Α ένας τετραγωνικός πίνακας. Το διάνυσμα v ονομάζεται ιδιοδιάνυσμαμήτρα Α εάν

Av = λv,

όπου ονομάζεται ο αριθμός λ ιδιοτιμήμήτρες Α. Έτσι, ο μετασχηματισμός που εκτελεί η μήτρα Α στο διάνυσμα v ανάγεται σε απλή διάταση ή συμπίεση με συντελεστή λ. Το ιδιοδιάνυσμα προσδιορίζεται μέχρι τον πολλαπλασιασμό με μια σταθερά α ≠ 0, δηλ. αν το v είναι ιδιοδιάνυσμα, τότε το αv είναι επίσης ιδιοδιάνυσμα.

2.7. Ιδιοτιμές

Ο πίνακας Α έχει διάσταση ( Ν× Ν) δεν μπορεί να είναι περισσότερο από Νιδιοτιμές. Ικανοποιούν χαρακτηριστική εξίσωση

det(A − λI ) = 0,

να εισαι αλγεβρική εξίσωση Ν-η σειρά. Συγκεκριμένα, για έναν πίνακα 2×2 η χαρακτηριστική εξίσωση έχει τη μορφή

Για παράδειγμα,

Ρύζι. 21 Ιδιοτιμές

Σύνολο ιδιοτιμών λ 1 ,..., λ Νκαλείται ο πίνακας Α φάσμαΕΝΑ.

Το φάσμα έχει διάφορες ιδιότητες. Συγκεκριμένα

det(A ) = λ 1 ×...×λ Ν, Sp(A ) = λ 1 +...+λ Ν.

Οι ιδιοτιμές ενός αυθαίρετου πίνακα μπορεί να είναι μιγαδικοί αριθμοί, αλλά αν ο πίνακας είναι συμμετρικός (A t = A), τότε οι ιδιοτιμές του είναι πραγματικές.

2.8. Ιδιοδιανύσματα

Ο πίνακας Α έχει διάσταση ( Ν× Ν) δεν μπορεί να είναι περισσότερο από Νιδιοδιανύσματα, καθένα από τα οποία αντιστοιχεί στη δική του ιδιοτιμή. Για να προσδιορίσετε το ιδιοδιάνυσμα v nχρειάζεται να λύσουμε ένα σύστημα ομοιογενών εξισώσεων

(Α − λ n I ) v n = 0 .

Έχει μια μη τετριμμένη λύση, αφού det(A − λ n I ) = 0.

Για παράδειγμα,

Ρύζι. 22 Ιδιοδιανύσματα

Τα ιδιοδιανύσματα ενός συμμετρικού πίνακα είναι ορθογώνια.

Οι διαγώνιοι πίνακες έχουν την απλούστερη δομή. Τίθεται το ερώτημα εάν είναι δυνατόν να βρεθεί μια βάση στην οποία ο πίνακας του γραμμικού τελεστή θα έχει διαγώνια μορφή. Μια τέτοια βάση υπάρχει.
Ας μας δοθεί ένας γραμμικός χώρος R n και ένας γραμμικός τελεστής A που ενεργεί σε αυτόν. Σε αυτή την περίπτωση, ο τελεστής A παίρνει το R n στον εαυτό του, δηλαδή, A:R n → R n .

Ορισμός. Ένα μη μηδενικό διάνυσμα ονομάζεται ιδιοδιάνυσμα του τελεστή Α εάν ο τελεστής Α μεταφράζεται σε συγγραμμικό διάνυσμα, δηλαδή. Ο αριθμός λ ονομάζεται ιδιοτιμή ή ιδιοτιμή του τελεστή Α, που αντιστοιχεί στο ιδιοδιάνυσμα.
Ας σημειώσουμε ορισμένες ιδιότητες των ιδιοτιμών και των ιδιοδιανυσμάτων.
1. Οποιοσδήποτε γραμμικός συνδυασμός ιδιοδιανυσμάτων Ο τελεστής Α που αντιστοιχεί στην ίδια ιδιοτιμή λ είναι ένα ιδιοδιάνυσμα με την ίδια ιδιοτιμή.
2. Ιδιοδιανύσματα Ο τελεστής Α με κατά ζεύγη διαφορετικές ιδιοτιμές λ 1 , λ 2 , …, λ m είναι γραμμικά ανεξάρτητοι.
3. Αν ιδιοτιμέςλ 1 =λ 2 = λ m = λ, τότε η ιδιοτιμή λ δεν αντιστοιχεί σε περισσότερα από m γραμμικά ανεξάρτητα ιδιοδιανύσματα.

Έτσι, εάν υπάρχουν n γραμμικά ανεξάρτητα ιδιοδιανύσματα , που αντιστοιχούν σε διαφορετικές ιδιοτιμές λ 1, λ 2, ..., λ n, τότε είναι γραμμικά ανεξάρτητες, επομένως, μπορούν να ληφθούν ως βάση του χώρου R n. Ας βρούμε τη μορφή του πίνακα του γραμμικού τελεστή Α στη βάση των ιδιοδιανυσμάτων του, για τον οποίο θα ενεργήσουμε με τον τελεστή Α στα διανύσματα βάσης: Επειτα .
Έτσι, ο πίνακας του γραμμικού τελεστή Α στη βάση των ιδιοδιανυσμάτων του έχει μια διαγώνια μορφή και οι ιδιοτιμές του τελεστή Α είναι κατά μήκος της διαγώνιας.
Υπάρχει άλλη βάση στην οποία ο πίνακας έχει διαγώνια μορφή; Η απάντηση σε αυτό το ερώτημα δίνεται από το παρακάτω θεώρημα.

Θεώρημα. Ο πίνακας ενός γραμμικού τελεστή Α στη βάση (i = 1..n) έχει διαγώνια μορφή αν και μόνο αν όλα τα διανύσματα της βάσης είναι ιδιοδιανύσματα του τελεστή Α.

Κανόνας εύρεσης ιδιοτιμών και ιδιοδιανυσμάτων Ας δοθεί ένα διάνυσμα , όπου x 1, x 2, …, x n είναι οι συντεταγμένες του διανύσματος σε σχέση με τη βάση και είναι το ιδιοδιάνυσμα του γραμμικού τελεστή Α που αντιστοιχεί στην ιδιοτιμή λ, δηλαδή. Αυτή η σχέση μπορεί να γραφτεί σε μορφή μήτρας

. (*)

Η εξίσωση (*) μπορεί να θεωρηθεί ως εξίσωση για την εύρεση , και, δηλαδή, μας ενδιαφέρει μη τετριμμένες λύσεις, αφού το ιδιοδιάνυσμα δεν μπορεί να είναι μηδέν. Είναι γνωστό ότι οι μη τετριμμένες λύσεις ομοιογενές σύστημαγραμμικές εξισώσεις υπάρχουν αν και μόνο αν det(A - λE) = 0. Έτσι, για να είναι το λ ιδιοτιμή του τελεστή A είναι απαραίτητο και αρκετό το det(A - λE) = 0.
Εάν η εξίσωση (*) είναι γραμμένη λεπτομερώς σε μορφή συντεταγμένων, παίρνουμε ένα σύστημα γραμμικών ομοιογενών εξισώσεων:

(1)
Οπου - γραμμικός πίνακας χειριστή.

Το σύστημα (1) έχει μη μηδενική λύση αν η ορίζοντή του D είναι ίση με μηδέν

Λάβαμε μια εξίσωση για την εύρεση ιδιοτιμών.
Αυτή η εξίσωση ονομάζεται χαρακτηριστική εξίσωση, και της αριστερή πλευρά- το χαρακτηριστικό πολυώνυμο του πίνακα (τελεστής) Α. Εάν το χαρακτηριστικό πολυώνυμο δεν έχει πραγματικές ρίζες, τότε ο πίνακας Α δεν έχει ιδιοδιανύσματα και δεν μπορεί να αναχθεί σε διαγώνια μορφή.
Έστω λ 1, λ 2, …, λ n οι πραγματικές ρίζες της χαρακτηριστικής εξίσωσης, και μεταξύ αυτών μπορεί να υπάρχουν πολλαπλάσια. Αντικαθιστώντας αυτές τις τιμές με τη σειρά τους στο σύστημα (1), βρίσκουμε τα ιδιοδιανύσματα.

Παράδειγμα 12. Ο γραμμικός τελεστής A δρα στο R 3 σύμφωνα με το νόμο, όπου x 1, x 2, .., x n είναι οι συντεταγμένες του διανύσματος στη βάση , , . Βρείτε τις ιδιοτιμές και τα ιδιοδιανύσματα αυτού του τελεστή.
Λύση. Κατασκευάζουμε τη μήτρα αυτού του τελεστή:
.
Δημιουργούμε ένα σύστημα για τον προσδιορισμό των συντεταγμένων των ιδιοδιανυσμάτων:

Συνθέτουμε μια χαρακτηριστική εξίσωση και τη λύνουμε:

.
λ 1,2 = -1, λ 3 = 3.
Αντικαθιστώντας το λ = -1 στο σύστημα, έχουμε:
ή
Επειδή , τότε υπάρχουν δύο εξαρτημένες μεταβλητές και μία ελεύθερη μεταβλητή.
Έστω το x 1 ένας ελεύθερος άγνωστος, λοιπόν Λύνουμε αυτό το σύστημα με κάθε τρόπο και βρίσκουμε κοινή απόφασηαυτού του συστήματος: Το θεμελιώδες σύστημα λύσεων αποτελείται από μία λύση, αφού n - r = 3 - 2 = 1.
Το σύνολο των ιδιοδιανυσμάτων που αντιστοιχεί στην ιδιοτιμή λ = -1 έχει τη μορφή: , όπου x 1 είναι οποιοσδήποτε αριθμός διαφορετικός από το μηδέν. Ας επιλέξουμε ένα διάνυσμα από αυτό το σύνολο, για παράδειγμα, βάζοντας x 1 = 1: .
Συλλογίζοντας παρόμοια, βρίσκουμε το ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή λ = 3: .
Στο χώρο R 3, η βάση αποτελείται από τρία γραμμικά ανεξάρτητα διανύσματα, αλλά λάβαμε μόνο δύο γραμμικά ανεξάρτητα ιδιοδιανύσματα, από τα οποία δεν μπορεί να συντεθεί η βάση στο R 3. Συνεπώς, δεν μπορούμε να μειώσουμε τον πίνακα Α ενός γραμμικού τελεστή σε διαγώνια μορφή.

Παράδειγμα 13. Δίνεται μια μήτρα .
1. Να αποδείξετε ότι το διάνυσμα είναι ένα ιδιοδιάνυσμα του πίνακα Α. Βρείτε την ιδιοτιμή που αντιστοιχεί σε αυτό το ιδιοδιάνυσμα.
2. Βρείτε μια βάση στην οποία ο πίνακας Α έχει διαγώνια μορφή.
Λύση.
1. Αν , τότε είναι ιδιοδιάνυσμα

.
Το διάνυσμα (1, 8, -1) είναι ένα ιδιοδιάνυσμα. Ιδιοτιμή λ = -1.
Ο πίνακας έχει μια διαγώνια μορφή σε μια βάση που αποτελείται από ιδιοδιανύσματα. Ένας από αυτούς είναι διάσημος. Ας βρούμε τα υπόλοιπα.
Αναζητούμε ιδιοδιανύσματα από το σύστημα:

Χαρακτηριστική εξίσωση: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Ας βρούμε το ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή λ = -3:

Η κατάταξη του πίνακα αυτού του συστήματος είναι δύο και ίση με τον αριθμό των αγνώστων, επομένως αυτό το σύστημα έχει μόνο μηδενική λύση x 1 = x 3 = 0. x 2 εδώ μπορεί να είναι οτιδήποτε άλλο εκτός από μηδέν, για παράδειγμα, x 2 = 1. Έτσι, το διάνυσμα (0 ,1,0) είναι ιδιοδιάνυσμα που αντιστοιχεί σε λ = -3. Ας ελέγξουμε:
.
Αν λ = 1, τότε παίρνουμε το σύστημα
Η κατάταξη του πίνακα είναι δύο. Διαγράφουμε την τελευταία εξίσωση.
Έστω x 3 ελεύθερος άγνωστος. Τότε x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Υποθέτοντας x 3 = 1, έχουμε (-3,-9,1) - ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή λ = 1. Ελέγξτε:

.
Δεδομένου ότι οι ιδιοτιμές είναι πραγματικές και διακριτές, τα διανύσματα που αντιστοιχούν σε αυτές είναι γραμμικά ανεξάρτητα, επομένως μπορούν να ληφθούν ως βάση στο R3. Έτσι, στη βάση , , Ο πίνακας Α έχει τη μορφή:
.
Δεν μπορεί κάθε πίνακας ενός γραμμικού τελεστή A:R n → R n να αναχθεί σε διαγώνια μορφή, αφού για ορισμένους γραμμικούς τελεστές μπορεί να υπάρχουν λιγότερα από n γραμμικά ανεξάρτητα ιδιοδιανύσματα. Ωστόσο, εάν ο πίνακας είναι συμμετρικός, τότε η ρίζα της χαρακτηριστικής εξίσωσης πολλαπλότητας m αντιστοιχεί ακριβώς σε m γραμμικά ανεξάρτητα διανύσματα.

Ορισμός. Ένας συμμετρικός πίνακας είναι ένας τετράγωνος πίνακας στον οποίο τα συμμετρικά στοιχεία ως προς την κύρια διαγώνιο είναι ίσα, δηλαδή στην οποία .
Σημειώσεις. 1. Όλες οι ιδιοτιμές ενός συμμετρικού πίνακα είναι πραγματικές.
2. Τα ιδιοδιανύσματα ενός συμμετρικού πίνακα που αντιστοιχεί σε διαφορετικές ιδιοτιμές ανά ζεύγη είναι ορθογώνια.
Ως μία από τις πολλές εφαρμογές της συσκευής που μελετήθηκε, θεωρούμε το πρόβλημα του προσδιορισμού του τύπου μιας καμπύλης δεύτερης τάξης.

Με τον πίνακα A, αν υπάρχει αριθμός l τέτοιος ώστε AX = lX.

Στην περίπτωση αυτή, ο αριθμός l ονομάζεται ιδιοτιμή του τελεστή (πίνακας Α), που αντιστοιχεί στο διάνυσμα X.

Με άλλα λόγια, ένα ιδιοδιάνυσμα είναι ένα διάνυσμα που, υπό τη δράση ενός γραμμικού τελεστή, μετατρέπεται σε συγγραμμικό διάνυσμα, δηλ. απλά πολλαπλασιάστε με κάποιο αριθμό. Αντίθετα, τα ακατάλληλα διανύσματα είναι πιο πολύπλοκα στον μετασχηματισμό.

Ας γράψουμε τον ορισμό ενός ιδιοδιανύσματος με τη μορφή ενός συστήματος εξισώσεων:

Ας μετακινήσουμε όλους τους όρους στην αριστερή πλευρά:

Το τελευταίο σύστημα μπορεί να γραφτεί σε μορφή μήτρας ως εξής:

(A - lE)X = O

Το σύστημα που προκύπτει έχει πάντα μηδενική λύση Χ = Ο. Τέτοια συστήματα στα οποία όλοι οι ελεύθεροι όροι είναι ίσοι με μηδέν ονομάζονται ομοιογενή. Εάν ο πίνακας ενός τέτοιου συστήματος είναι τετράγωνος και η ορίζουσα του δεν είναι ίση με το μηδέν, τότε χρησιμοποιώντας τους τύπους του Cramer θα έχουμε πάντα μια μοναδική λύση - μηδέν. Μπορεί να αποδειχθεί ότι ένα σύστημα έχει μη μηδενικές λύσεις εάν και μόνο εάν η ορίζουσα αυτού του πίνακα είναι ίση με μηδέν, δηλ.

|A - lE| = = 0

Αυτή η εξίσωση με άγνωστο l ονομάζεται χαρακτηριστική εξίσωση (χαρακτηριστικό πολυώνυμο) του πίνακα Α (γραμμικός τελεστής).

Μπορεί να αποδειχθεί ότι το χαρακτηριστικό πολυώνυμο ενός γραμμικού τελεστή δεν εξαρτάται από την επιλογή της βάσης.

Για παράδειγμα, ας βρούμε τις ιδιοτιμές και τα ιδιοδιανύσματα του γραμμικού τελεστή που ορίζονται από τον πίνακα A = .

Για να γίνει αυτό, ας δημιουργήσουμε μια χαρακτηριστική εξίσωση |A - lE| = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; ιδιοτιμές l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.

Για να βρούμε ιδιοδιανύσματα, λύνουμε δύο συστήματα εξισώσεων

(A + 5E)X = O

(A - 7E)X = O

Για το πρώτο από αυτά, ο διευρυμένος πίνακας παίρνει τη μορφή

,

από όπου x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, δηλ. X (1) = (-(2/3)s; s).

Για το δεύτερο από αυτά, ο διευρυμένος πίνακας παίρνει τη μορφή

,

από όπου x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, δηλ. X (2) = ((2/3)s 1, s 1).

Έτσι, τα ιδιοδιανύσματα αυτού του γραμμικού τελεστή είναι όλα διανύσματα της μορφής (-(2/3)с; γ) με ιδιοτιμή (-5) και όλα τα διανύσματα της μορφής ((2/3)с 1 ; с 1) με ιδιοτιμή 7 .

Μπορεί να αποδειχθεί ότι ο πίνακας του τελεστή Α στη βάση που αποτελείται από τα ιδιοδιανύσματά του είναι διαγώνιος και έχει τη μορφή:

,

όπου l i είναι οι ιδιοτιμές αυτού του πίνακα.

Το αντίστροφο ισχύει επίσης: εάν ο πίνακας Α σε κάποια βάση είναι διαγώνιος, τότε όλα τα διανύσματα αυτής της βάσης θα είναι ιδιοδιανύσματα αυτού του πίνακα.

Μπορεί επίσης να αποδειχθεί ότι εάν ένας γραμμικός τελεστής έχει n κατά ζεύγη διακριτές ιδιοτιμές, τότε τα αντίστοιχα ιδιοδιανύσματα είναι γραμμικά ανεξάρτητα και ο πίνακας αυτού του τελεστή στην αντίστοιχη βάση έχει διαγώνια μορφή.

Ας το επεξηγήσουμε αυτό με το προηγούμενο παράδειγμα. Ας πάρουμε αυθαίρετες μη μηδενικές τιμές c και c 1, αλλά τέτοιες ώστε τα διανύσματα X (1) και X (2) να είναι γραμμικά ανεξάρτητα, δηλ. θα αποτελούσε βάση. Για παράδειγμα, έστω c = c 1 = 3, μετά X (1) = (-2; 3), X (2) = (2; 3).

Ας επαληθεύσουμε τη γραμμική ανεξαρτησία αυτών των διανυσμάτων:

12 ≠ 0. Σε αυτή τη νέα βάση, ο πίνακας A θα έχει τη μορφή A * = .

Για να το επαληθεύσουμε αυτό, ας χρησιμοποιήσουμε τον τύπο A * = C -1 AC. Αρχικά, ας βρούμε το C -1.

C-1 = ;

Τετραγωνικά σχήματα

Η τετραγωνική μορφή f(x 1, x 2, x n) των n μεταβλητών είναι ένα άθροισμα, κάθε όρος του οποίου είναι είτε το τετράγωνο μιας από τις μεταβλητές ή το γινόμενο δύο διαφορετικών μεταβλητών, που λαμβάνονται με έναν ορισμένο συντελεστή: f( x 1, x 2, x n ) = (a ij = a ji).

Ο πίνακας Α που αποτελείται από αυτούς τους συντελεστές ονομάζεται πίνακας τετραγωνικής μορφής. Αυτός είναι πάντα ένας συμμετρικός πίνακας (δηλαδή ένας πίνακας συμμετρικός ως προς την κύρια διαγώνιο, a ij = a ji).

Στον συμβολισμό πίνακα, η τετραγωνική μορφή είναι f(X) = X T AX, όπου

Πράγματι

Για παράδειγμα, ας γράψουμε την τετραγωνική μορφή σε μορφή πίνακα.

Για να γίνει αυτό, βρίσκουμε έναν πίνακα τετραγωνικής μορφής. Τα διαγώνια στοιχεία του είναι ίσα με τους συντελεστές των τετραγωνικών μεταβλητών και τα υπόλοιπα στοιχεία είναι ίσα με τα μισά των αντίστοιχων συντελεστών της τετραγωνικής μορφής. Να γιατί

Έστω ότι η μήτρα-στήλη των μεταβλητών X λαμβάνεται από έναν μη εκφυλισμένο γραμμικό μετασχηματισμό της μήτρας-στήλης Υ, δηλ. X = CY, όπου C είναι ένας μη ενικός πίνακας νης τάξης. Τότε η τετραγωνική μορφή f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Έτσι, με έναν μη εκφυλισμένο γραμμικό μετασχηματισμό C, ο πίνακας τετραγωνικής μορφής παίρνει τη μορφή: A * = C T AC.

Για παράδειγμα, ας βρούμε την τετραγωνική μορφή f(y 1, y 2), που προκύπτει από την τετραγωνική μορφή f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 με γραμμικό μετασχηματισμό.

Μια τετραγωνική μορφή ονομάζεται κανονική (έχει κανονική μορφή) αν όλοι οι συντελεστές της a ij = 0 για i ≠ j, δηλ.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .

Η μήτρα του είναι διαγώνιος.

Θεώρημα (η απόδειξη δεν δίνεται εδώ). Οποιαδήποτε τετραγωνική μορφή μπορεί να αναχθεί σε κανονική μορφή χρησιμοποιώντας έναν μη εκφυλισμένο γραμμικό μετασχηματισμό.

Για παράδειγμα, ας ανάγουμε την τετραγωνική μορφή σε κανονική μορφή
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Για να το κάνετε αυτό, επιλέξτε πρώτα ένα πλήρες τετράγωνο με τη μεταβλητή x 1:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Τώρα επιλέγουμε ένα πλήρες τετράγωνο με τη μεταβλητή x 2:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5 (x 2 - (1/10)x 3) 2 + (1/20) x 3 2.

Τότε ο μη εκφυλισμένος γραμμικός μετασχηματισμός y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 και y 3 = x 3 φέρνει αυτήν την τετραγωνική μορφή στην κανονική μορφή f(y 1, y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Σημειώστε ότι η κανονική μορφή μιας τετραγωνικής μορφής καθορίζεται διφορούμενα (η ίδια τετραγωνική μορφή μπορεί να αναχθεί στην κανονική μορφή διαφορετικοί τρόποι). Ωστόσο, το έλαβε διαφορετικοί τρόποιοι κανονικές μορφές έχουν έναν αριθμό από γενικές ιδιότητες. Συγκεκριμένα, ο αριθμός των όρων με θετικούς (αρνητικούς) συντελεστές μιας τετραγωνικής μορφής δεν εξαρτάται από τη μέθοδο αναγωγής της φόρμας σε αυτήν τη μορφή (για παράδειγμα, στο εξεταζόμενο παράδειγμα θα υπάρχουν πάντα δύο αρνητικοί και ένας θετικός συντελεστής). Αυτή η ιδιότητα ονομάζεται νόμος της αδράνειας των τετραγωνικών μορφών.

Ας το επαληθεύσουμε αυτό φέρνοντας την ίδια τετραγωνική μορφή στην κανονική μορφή με διαφορετικό τρόπο. Ας ξεκινήσουμε τον μετασχηματισμό με τη μεταβλητή x 2:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, όπου y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 και y 3 = x 1 . Εδώ υπάρχει ένας αρνητικός συντελεστής -3 στο y 1 και δύο θετικοί συντελεστές 3 και 2 στο y 2 και y 3 (και χρησιμοποιώντας μια άλλη μέθοδο πήραμε έναν αρνητικό συντελεστή (-5) στο y 2 και δύο θετικούς: 2 στο y 1 και 1/20 στο y 3).

Θα πρέπει επίσης να σημειωθεί ότι η κατάταξη ενός πίνακα μιας τετραγωνικής μορφής, που ονομάζεται κατάταξη της τετραγωνικής μορφής, είναι ίση με τον αριθμό των μη μηδενικών συντελεστών της κανονικής μορφής και δεν αλλάζει υπό γραμμικούς μετασχηματισμούς.

Μια τετραγωνική μορφή f(X) ονομάζεται θετική (αρνητική) οριστική αν για όλες τις τιμές των μεταβλητών που δεν είναι ταυτόχρονα ίσες με μηδέν, είναι θετική, δηλ. f(X) > 0 (αρνητικό, δηλ.
f(X)< 0).

Για παράδειγμα, η τετραγωνική μορφή f 1 (X) = x 1 2 + x 2 2 είναι θετική οριστική, επειδή είναι ένα άθροισμα τετραγώνων και η τετραγωνική μορφή f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 είναι αρνητική οριστική, επειδή αντιπροσωπεύει μπορεί να αναπαρασταθεί ως f 2 (X) = -(x 1 - x 2) 2.

Στην πλειοψηφία πρακτικές καταστάσειςΕίναι κάπως πιο δύσκολο να καθορίσουμε το οριστικό πρόσημο μιας τετραγωνικής μορφής, γι' αυτό χρησιμοποιούμε ένα από τα παρακάτω θεωρήματα (θα τα διατυπώσουμε χωρίς απόδειξη).

Θεώρημα. Μια τετραγωνική μορφή είναι θετική (αρνητική) ορισμένη αν και μόνο αν όλες οι ιδιοτιμές του πίνακα της είναι θετικές (αρνητικές).

Θεώρημα (κριτήριο Sylvester). Μια τετραγωνική μορφή είναι θετική ορισμένη αν και μόνο αν όλα τα κύρια δευτερεύοντα του πίνακα αυτής της μορφής είναι θετικά.

Η κύρια (γωνιακή) ελάσσονα της kth τάξης του πίνακα nης τάξης A είναι η ορίζουσα του πίνακα, που αποτελείται από τις πρώτες k σειρές και στήλες του πίνακα A ().

Σημειώστε ότι για αρνητικούς οριστικούς τετραγωνικούς τύπους τα πρόσημα των κυρίων ανηλίκων εναλλάσσονται και το δευτερεύον πρώτης τάξης πρέπει να είναι αρνητικό.

Για παράδειγμα, ας εξετάσουμε την τετραγωνική μορφή f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 για την οριστικότητα του πρόσημου.

= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
. Επομένως, η τετραγωνική μορφή είναι θετική οριστική.

Μέθοδος 2. Κύρια ελάσσονα πρώτης τάξης του πίνακα A D 1 = a 11 = 2 > 0. Κύριο ελάσσονα δεύτερης τάξης D 2 = = 6 - 4 = 2 > 0. Επομένως, σύμφωνα με το κριτήριο του Sylvester, η τετραγωνική μορφή είναι θετική οριστική.

Εξετάζουμε μια άλλη τετραγωνική μορφή για την οριστικότητα του πρόσημου, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Μέθοδος 1. Ας κατασκευάσουμε έναν πίνακα τετραγωνικής μορφής A = . Η χαρακτηριστική εξίσωση θα έχει τη μορφή = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Επομένως, η τετραγωνική μορφή είναι αρνητική οριστική.

Μέθοδος 2. Κύριο δευτερεύον της πρώτης τάξης του πίνακα A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Κατά συνέπεια, σύμφωνα με το κριτήριο του Sylvester, η τετραγωνική μορφή είναι αρνητική οριστική (τα πρόσημα των κύριων ανηλίκων εναλλάσσονται, ξεκινώντας από το μείον).

Και ως άλλο παράδειγμα, ας εξετάσουμε τη μορφή οριστικής προσήμου f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2.

Μέθοδος 1. Ας κατασκευάσουμε έναν πίνακα τετραγωνικής μορφής A = . Η χαρακτηριστική εξίσωση θα έχει τη μορφή = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Ο ένας από αυτούς τους αριθμούς είναι αρνητικός και ο άλλος θετικός. Τα σημάδια των ιδιοτιμών είναι διαφορετικά. Κατά συνέπεια, η τετραγωνική μορφή δεν μπορεί να είναι ούτε αρνητικά ούτε θετικά οριστική, δηλ. αυτή η τετραγωνική μορφή δεν είναι καθορισμένη (μπορεί να πάρει τιμές οποιουδήποτε σημείου).

Μέθοδος 2. Κύρια ελάσσονα πρώτης τάξης του πίνακα A D 1 = a 11 = 2 > 0. Κύρια ελάσσονα δεύτερης τάξης D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Πώς να εισάγετε μαθηματικούς τύπους σε έναν ιστότοπο;

Εάν χρειαστεί ποτέ να προσθέσετε έναν ή δύο μαθηματικούς τύπους σε μια ιστοσελίδα, τότε ο ευκολότερος τρόπος για να το κάνετε αυτό είναι όπως περιγράφεται στο άρθρο: οι μαθηματικοί τύποι εισάγονται εύκολα στον ιστότοπο με τη μορφή εικόνων που δημιουργούνται αυτόματα από το Wolfram Alpha . Εκτός από την απλότητα, αυτή η καθολική μέθοδος θα βοηθήσει στη βελτίωση της προβολής του ιστότοπου στις μηχανές αναζήτησης. Λειτουργεί εδώ και πολύ καιρό (και, νομίζω, θα λειτουργεί για πάντα), αλλά είναι ήδη ηθικά ξεπερασμένο.

Εάν χρησιμοποιείτε τακτικά μαθηματικούς τύπους στον ιστότοπό σας, τότε σας συνιστώ να χρησιμοποιήσετε το MathJax - μια ειδική βιβλιοθήκη JavaScript που εμφανίζει μαθηματικούς σημειώσεις σε προγράμματα περιήγησης ιστού χρησιμοποιώντας σήμανση MathML, LaTeX ή ASCIIMathML.

Υπάρχουν δύο τρόποι για να ξεκινήσετε να χρησιμοποιείτε το MathJax: (1) χρησιμοποιώντας έναν απλό κώδικα, μπορείτε να συνδέσετε γρήγορα ένα σενάριο MathJax στον ιστότοπό σας, το οποίο θα φορτωθεί αυτόματα από έναν απομακρυσμένο διακομιστή την κατάλληλη στιγμή (λίστα διακομιστών). (2) κατεβάστε το σενάριο MathJax από έναν απομακρυσμένο διακομιστή στον διακομιστή σας και συνδέστε το σε όλες τις σελίδες του ιστότοπού σας. Η δεύτερη μέθοδος - πιο περίπλοκη και χρονοβόρα - θα επιταχύνει τη φόρτωση των σελίδων του ιστότοπού σας και εάν ο γονικός διακομιστής MathJax γίνει προσωρινά μη διαθέσιμος για κάποιο λόγο, αυτό δεν θα επηρεάσει με κανέναν τρόπο τον δικό σας ιστότοπο. Παρά τα πλεονεκτήματα αυτά, επέλεξα την πρώτη μέθοδο καθώς είναι πιο απλή, πιο γρήγορη και δεν απαιτεί τεχνικές δεξιότητες. Ακολουθήστε το παράδειγμά μου και σε μόλις 5 λεπτά θα μπορείτε να χρησιμοποιήσετε όλες τις δυνατότητες του MathJax στον ιστότοπό σας.

Μπορείτε να συνδέσετε το σενάριο της βιβλιοθήκης MathJax από έναν απομακρυσμένο διακομιστή χρησιμοποιώντας δύο επιλογές κώδικα που λαμβάνονται από τον κύριο ιστότοπο του MathJax ή από τη σελίδα τεκμηρίωσης:

Μία από αυτές τις επιλογές κώδικα πρέπει να αντιγραφεί και να επικολληθεί στον κώδικα της ιστοσελίδας σας, κατά προτίμηση μεταξύ ετικετών και ή αμέσως μετά την ετικέτα. Σύμφωνα με την πρώτη επιλογή, το MathJax φορτώνει πιο γρήγορα και επιβραδύνει λιγότερο τη σελίδα. Αλλά η δεύτερη επιλογή παρακολουθεί αυτόματα και φορτώνει τις πιο πρόσφατες εκδόσεις του MathJax. Εάν εισάγετε τον πρώτο κωδικό, θα πρέπει να ενημερώνεται περιοδικά. Εάν εισαγάγετε τον δεύτερο κώδικα, οι σελίδες θα φορτώνονται πιο αργά, αλλά δεν θα χρειάζεται να παρακολουθείτε συνεχώς τις ενημερώσεις του MathJax.

Ο ευκολότερος τρόπος σύνδεσης του MathJax είναι στο Blogger ή στο WordPress: στον πίνακα ελέγχου του ιστότοπου, προσθέστε ένα γραφικό στοιχείο σχεδιασμένο για την εισαγωγή κώδικα JavaScript τρίτου μέρους, αντιγράψτε την πρώτη ή τη δεύτερη έκδοση του κώδικα λήψης που παρουσιάζεται παραπάνω σε αυτό και τοποθετήστε το γραφικό στοιχείο πιο κοντά στην αρχή του προτύπου (παρεμπιπτόντως, αυτό δεν είναι καθόλου απαραίτητο, καθώς το σενάριο MathJax φορτώνεται ασύγχρονα). Αυτό είναι όλο. Τώρα μάθετε τη σύνταξη σήμανσης των MathML, LaTeX και ASCIIMathML και είστε έτοιμοι να εισαγάγετε μαθηματικούς τύπους στις ιστοσελίδες του ιστότοπού σας.

Οποιοδήποτε φράκταλ κατασκευάζεται σύμφωνα με έναν ορισμένο κανόνα, το οποίο εφαρμόζεται διαδοχικά απεριόριστες φορές. Κάθε τέτοιος χρόνος ονομάζεται επανάληψη.

Ο επαναληπτικός αλγόριθμος για την κατασκευή ενός σφουγγαριού Menger είναι αρκετά απλός: ο αρχικός κύβος με την πλευρά 1 χωρίζεται με επίπεδα παράλληλα προς τις όψεις του σε 27 ίσους κύβους. Ένας κεντρικός κύβος και 6 κύβοι δίπλα του κατά μήκος των όψεων αφαιρούνται από αυτό. Το αποτέλεσμα είναι ένα σετ που αποτελείται από τους υπόλοιπους 20 μικρότερους κύβους. Κάνοντας το ίδιο με κάθε έναν από αυτούς τους κύβους, παίρνουμε ένα σετ που αποτελείται από 400 μικρότερους κύβους. Συνεχίζοντας αυτή τη διαδικασία ατελείωτα, παίρνουμε ένα σφουγγάρι Menger.