Articolul oferă o explicație detaliată a definițiilor, semnificația geometrică a derivatei cu notații grafice. Ecuația unei linii tangente va fi luată în considerare cu exemple, se vor găsi ecuațiile unei tangente la curbele de ordinul 2.
Yandex.RTB R-A-339285-1 Definiție 1
Unghiul de înclinare al dreptei y = k x + b se numește unghi α, care se măsoară de la direcția pozitivă a axei x la dreapta y = k x + b în direcția pozitivă.
În figură, direcția x este indicată printr-o săgeată verde și un arc verde, iar unghiul de înclinare printr-un arc roșu. Linia albastră se referă la linia dreaptă.
Definiția 2
Panta dreptei y = k x + b se numește coeficient numeric k.
Coeficientul unghiular este egal cu tangentei dreptei, cu alte cuvinte k = t g α.
- Unghiul de înclinare al unei drepte este egal cu 0 numai dacă este paralelă în jurul lui x și panta este egală cu zero, deoarece tangenta lui zero este egală cu 0. Aceasta înseamnă că forma ecuației va fi y = b.
- Dacă unghiul de înclinare al dreptei y = k x + b este acut, atunci condițiile 0 sunt îndeplinite< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 și există o creștere a graficului.
- Dacă α = π 2, atunci locația dreptei este perpendiculară pe x. Egalitatea este specificată de x = c, valoarea c fiind un număr real.
- Dacă unghiul de înclinare al dreptei y = k x + b este obtuz, atunci corespunde condițiilor π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
O secantă este o dreaptă care trece prin 2 puncte ale funcției f (x). Cu alte cuvinte, o secanta este o linie dreaptă care este trasată prin oricare două puncte de pe grafic funcţie dată.

Figura arată că A B este o secante, iar f (x) este o curbă neagră, α este un arc roșu, indicând unghiul de înclinare al secantei.
Când coeficientul unghiular al unei drepte este egal cu tangentei unghiului de înclinare, este clar că tangentei unui triunghi dreptunghic A B C se poate găsi prin raportul dintre latura opusă față de cea adiacentă.
Definiția 4
Obținem o formulă pentru găsirea unei secante de forma:
k = t g α = B C A C = f (x B) - f x A x B - x A, unde abscisele punctelor A și B sunt valorile x A, x B și f (x A), f (x B) sunt funcțiile de valori în aceste puncte.
Evident, coeficientul unghiular al secantei este determinat folosind egalitatea k = f (x B) - f (x A) x B - x A sau k = f (x A) - f (x B) x A - x B , iar ecuația trebuie scrisă ca y = f (x B) - f (x A) x B - x A x - x A + f (x A) sau
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .
Secanta împarte graficul vizual în 3 părți: la stânga punctului A, de la A la B, la dreapta lui B. Figura de mai jos arată că există trei secante care sunt considerate coincidente, adică sunt stabilite folosind un ecuație similară.

Prin definiție, este clar că linia dreaptă și secanta ei în acest caz coincid.
O secanta poate intersecta graficul unei funcții date de mai multe ori. Dacă există o ecuație de forma y = 0 pentru o secantă, atunci numărul de puncte de intersecție cu sinusoida este infinit.
Definiția 5
Tangenta la graficul functiei f (x) in punctul x 0 ; f (x 0) este o dreaptă care trece printr-un punct dat x 0; f (x 0), cu prezența unui segment care are multe valori x apropiate de x 0.
Exemplul 1
Să aruncăm o privire mai atentă la exemplul de mai jos. Atunci este clar că linia definită de funcția y = x + 1 este considerată tangentă la y = 2 x în punctul cu coordonatele (1; 2). Pentru claritate, este necesar să luați în considerare graficele cu valori apropiate de (1; 2). Funcția y = 2 x este afișată cu negru, linia albastră este linia tangentă, iar punctul roșu este punctul de intersecție.

Evident, y = 2 x se îmbină cu linia y = x + 1.
Pentru a determina tangentei, ar trebui să luăm în considerare comportamentul tangentei A B pe măsură ce punctul B se apropie la infinit de punctul A. Pentru claritate, prezentăm un desen.

Secanta A B, indicată de linia albastră, tinde spre poziția tangentei însăși, iar unghiul de înclinare al secantei α va începe să tinde spre unghiul de înclinare al tangentei însăși α x.
Definiția 6
Tangenta la graficul funcției y = f (x) în punctul A este considerată a fi poziția limită a secantei A B, deoarece B tinde spre A, adică B → A.
Acum să trecem la considerarea semnificației geometrice a derivatei unei funcții într-un punct.
Să trecem la considerarea secantei A B pentru funcția f (x), unde A și B cu coordonatele x 0, f (x 0) și x 0 + ∆ x, f (x 0 + ∆ x) și ∆ x este notat ca increment al argumentului . Acum funcția va lua forma ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Pentru claritate, să dăm un exemplu de desen.

Să luăm în considerare rezultatul triunghi dreptunghic A B C. Folosim definiția tangentei pentru a rezolva, adică obținem relația ∆ y ∆ x = t g α . Din definiția unei tangente rezultă că lim ∆ x → 0 ∆ y ∆ x = t g α x . Conform regulii derivatei într-un punct, avem că derivata f (x) în punctul x 0 se numește limita raportului dintre incrementul funcției și incrementul argumentului, unde ∆ x → 0 , atunci o notăm f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Rezultă că f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, unde k x este notat ca panta tangentei.
Adică, obținem că f ’ (x) poate exista în punctul x 0 și ca tangenta la programul dat funcția în punctul de tangență egală cu x 0, f 0 (x 0), unde valoarea pantei tangentei în punctul este egală cu derivata în punctul x 0. Atunci obținem că k x = f " (x 0) .
Sensul geometric al derivatei unei funcții într-un punct este că dă conceptul existenței unei tangente la grafic în același punct.
Pentru a scrie ecuația oricărei drepte pe un plan, este necesar să existe un coeficient unghiular cu punctul prin care trece. Notația sa este considerată x 0 la intersecție.
Ecuația tangentă la graficul funcției y = f (x) în punctul x 0, f 0 (x 0) ia forma y = f "(x 0) x - x 0 + f (x 0).
Aceasta înseamnă că valoarea finală a derivatei f „(x 0) poate determina poziția tangentei, adică pe verticală, cu condiția lim x → x 0 + 0 f „(x) = ∞ și lim x → x 0 - 0 f "(x ) = ∞ sau absență deloc în condiția lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .
Locația tangentei depinde de valoarea coeficientului ei unghiular k x = f "(x 0). Când este paralelă cu axa o x, obținem că k k = 0, când paralel cu o y - k x = ∞ și forma ecuația tangentă x = x 0 crește cu k x > 0, scade pe măsură ce k x< 0 .
Exemplul 2
Alcătuiți o ecuație pentru tangenta la graficul funcției y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 în punctul cu coordonatele (1; 3) și determinați unghiul de înclinare.
Soluţie
Prin condiție, avem că funcția este definită pentru toate numerele reale. Constatăm că punctul cu coordonatele specificate de condiția, (1; 3) este un punct de tangență, atunci x 0 = - 1, f (x 0) = - 3.
Este necesar să găsiți derivata în punctul cu valoarea - 1. Înțelegem asta
y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Valoarea lui f' (x) în punctul de tangență este panta tangentei, care este egală cu tangentei pantei.
Atunci k x = t g α x = y " (x 0) = 3 3
Rezultă că α x = a r c t g 3 3 = π 6
Răspuns: ecuația tangentei ia forma
y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3
Pentru claritate, dăm un exemplu într-o ilustrație grafică.
Culoarea neagră este folosită pentru graficul funcției originale, Culoarea albastră– imaginea unei tangente, punct roșu – punct de tangență. Figura din dreapta arată o vedere mărită.

Exemplul 3
Determinați existența unei tangente la graficul unei funcții date
y = 3 · x - 1 5 + 1 în punctul cu coordonatele (1 ; 1) . Scrieți o ecuație și determinați unghiul de înclinare.
Soluţie
Prin condiție, avem că domeniul de definire al unei funcții date este considerat a fi mulțimea tuturor numerelor reale.
Să trecem la găsirea derivatei
y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Dacă x 0 = 1, atunci f' (x) este nedefinit, dar limitele sunt scrise ca lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ și lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , ceea ce înseamnă existența tangentă verticală în punctul (1; 1).
Răspuns: ecuația va lua forma x = 1, unde unghiul de înclinare va fi egal cu π 2.
Pentru claritate, să-l descriem grafic.

Exemplul 4
Aflați punctele de pe graficul funcției y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, unde
- Nu există tangentă;
- Tangenta este paralelă cu x;
- Tangenta este paralelă cu dreapta y = 8 5 x + 4.
Soluţie
Este necesar să se acorde atenție domeniului de aplicare al definiției. Prin condiție, avem că funcția este definită pe mulțimea tuturor numerelor reale. Extindem modulul și rezolvăm sistemul cu intervale x ∈ - ∞ ; 2 şi [-2; + ∞). Înțelegem asta
y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)
Este necesar să se diferențieze funcția. Avem asta
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)
Când x = − 2, atunci derivata nu există deoarece limitele unilaterale nu sunt egale în acel punct:
lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Calculăm valoarea funcției în punctul x = - 2, de unde obținem asta
- y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, adică tangenta în punctul ( - 2; - 2) nu va exista.
- Tangenta este paralelă cu x când panta este zero. Atunci k x = t g α x = f "(x 0). Adică, este necesar să se găsească valorile unui astfel de x atunci când derivata funcției o transformă la zero. Adică, valorile lui f ' (x) vor fi punctele de tangență, unde tangenta este paralelă cu x .
Când x ∈ - ∞ ; - 2, atunci - 1 5 (x 2 + 12 x + 35) = 0, iar pentru x ∈ (- 2; + ∞) obținem 1 5 (x 2 - 4 x + 3) = 0.
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Calculați valorile funcției corespunzătoare
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Prin urmare - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 sunt considerate a fi punctele necesare ale graficului funcției.
Să ne uităm la o reprezentare grafică a soluției.

Linia neagră este graficul funcției, punctele roșii sunt punctele de tangență.
- Când liniile sunt paralele, coeficienții unghiulari sunt egali. Apoi este necesar să căutați puncte pe graficul funcției unde panta va fi egală cu valoarea 8 5. Pentru a face acest lucru, trebuie să rezolvați o ecuație de forma y "(x) = 8 5. Atunci, dacă x ∈ - ∞; - 2, obținem că - 1 5 (x 2 + 12 x + 35) = 8 5, iar dacă x ∈ ( - 2 ; + ∞), atunci 1 5 (x 2 - 4 x + 3) = 8 5.
Prima ecuație nu are rădăcini, deoarece discriminantul mai putin de zero. Să scriem asta
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
O altă ecuație are două rădăcini reale, deci
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Să trecem la găsirea valorilor funcției. Înțelegem asta
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Puncte cu valori - 1; 4 15, 5; 8 3 sunt punctele în care tangentele sunt paralele cu dreapta y = 8 5 x + 4.
Răspuns: linie neagră – graficul funcției, linie roșie – graficul lui y = 8 5 x + 4, linie albastră – tangente în puncte - 1; 4 15, 5; 8 3.

Poate exista un număr infinit de tangente pentru funcții date.
Exemplul 5
Scrieți ecuațiile tuturor tangentelor disponibile ale funcției y = 3 cos 3 2 x - π 4 - 1 3, care sunt situate perpendicular pe dreapta y = - 2 x + 1 2.
Soluţie
Pentru a compila ecuația tangentei, este necesar să se găsească coeficientul și coordonatele punctului tangente, pe baza condiției de perpendicularitate a dreptelor. Definiția este următoarea: produsul coeficienților unghiulari care sunt perpendiculari pe liniile drepte este egal cu - 1, adică scris ca k x · k ⊥ = - 1. Din condiția avem că coeficientul unghiular este situat perpendicular pe dreapta și este egal cu k ⊥ = - 2, atunci k x = - 1 k ⊥ = - 1 - 2 = 1 2.
Acum trebuie să găsiți coordonatele punctelor de atingere. Trebuie să găsiți x și apoi valoarea lui pentru o funcție dată. Rețineți că din sensul geometric al derivatei la punct
x 0 obținem că k x = y "(x 0). Din această egalitate găsim valorile lui x pentru punctele de contact.
Înțelegem asta
y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9
Acest ecuație trigonometrică va fi folosit pentru calcularea ordonatelor punctelor tangente.
3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk sau 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk sau 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk sau x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z este o mulțime de numere întregi.
au fost găsite x puncte de contact. Acum trebuie să treceți la căutarea valorilor lui y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 sau y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 sau y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 sau y 0 = - 4 5 + 1 3
Din aceasta obținem că 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 sunt punctele de tangență.
Răspuns: ecuaţiile necesare se vor scrie ca
y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
Pentru o reprezentare vizuală, luați în considerare o funcție și o tangentă pe o dreaptă de coordonate.
Figura arată că funcţia este situată pe intervalul [ - 10 ; 10 ], unde linia neagră este graficul funcției, liniile albastre sunt tangente, care sunt situate perpendicular pe dreapta dată de forma y = - 2 x + 1 2. Punctele roșii sunt puncte de atingere.

Ecuațiile canonice ale curbelor de ordinul 2 nu sunt funcții cu o singură valoare. Ecuațiile tangente pentru ele sunt compilate conform schemelor cunoscute.
Tangent la un cerc
A defini un cerc cu centru în punctul x c e n t e r ; y c e n t e r şi raza R, aplicaţi formula x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .
Această egalitate poate fi scrisă ca o unire a două funcții:
y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r
Prima funcție este situată în partea de sus, iar a doua în partea de jos, așa cum se arată în figură.

Pentru a compila ecuația unui cerc în punctul x 0; y 0 , care este situat în semicercul superior sau inferior, ar trebui să găsiți ecuația graficului unei funcții de forma y = R 2 - x - x c e n t e r 2 + y c e n t e r sau y = - R 2 - x - x c e n t e r 2 + y c e n t e r la punctul indicat.
Când în punctele x c e n t e r ; y c e n t e r + R și x ce n t e r ; y c e n t e r - R tangente pot fi date de ecuațiile y = y c e n t e r + R și y = y c e n t e r - R , iar în punctele x c e n t e r + R ; y c e n t e r şi
x c e n t e r - R ; y c e n t e r va fi paralel cu o y, atunci obținem ecuații de forma x = x c e n t e r + R și x = x c e n t e r - R .

Tangent la o elipsă
Când elipsa are un centru în x c e n t e r ; y c e n t e r cu semiaxele a și b, atunci poate fi specificat folosind ecuația x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.
O elipsă și un cerc pot fi notate prin combinarea a două funcții, și anume semielipsa superioară și inferioară. Atunci obținem asta
y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Dacă tangentele sunt situate la vârfurile elipsei, atunci ele sunt paralele cu x sau despre y. Mai jos, pentru claritate, luați în considerare figura.

Exemplul 6
Scrieți ecuația tangentei la elipsa x - 3 2 4 + y - 5 2 25 = 1 în punctele cu valorile lui x egale cu x = 2.
Soluţie
Este necesar să găsiți punctele tangente care corespund valorii x = 2. Substituim în ecuația existentă a elipsei și aflăm că
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Apoi 2; 5 3 2 + 5 și 2; - 5 3 2 + 5 sunt punctele tangente care aparțin semielipsei superioare și inferioare.
Să trecem la găsirea și rezolvarea ecuației elipsei în raport cu y. Înțelegem asta
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Evident, semielipsa superioară este specificată folosind o funcție de forma y = 5 + 5 2 4 - x - 3 2, iar jumătatea inferioară y = 5 - 5 2 4 - x - 3 2.
Să aplicăm un algoritm standard pentru a crea o ecuație pentru o tangentă la graficul unei funcții într-un punct. Să scriem că ecuația pentru prima tangentă la punctul 2; 5 3 2 + 5 vor arăta ca
y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Constatăm că ecuația celei de-a doua tangente cu o valoare în punct
2; - 5 3 2 + 5 ia forma
y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Grafic, tangentele sunt desemnate după cum urmează:

Tangenta la hiperbola
Când o hiperbolă are un centru în x c e n t e r ; y c e n t e r şi vârfuri x c e n t e r + α ; y c e n t e r şi x c e n t e r - α ; y c e n t e r , are loc inegalitatea x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, dacă cu vârfuri x c e n t e r ; y c e n t e r + b și x c e n t e r ; y c e n t e r - b , atunci este specificat folosind inegalitatea x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

O hiperbolă poate fi reprezentată ca două funcții combinate ale formei
y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r sau y = b a · (x - x c e n t e r) 2 + a 2 + y c e n t e · r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

În primul caz avem că tangentele sunt paralele cu y, iar în al doilea sunt paralele cu x.
Rezultă că pentru a găsi ecuația tangentei la o hiperbolă este necesar să aflăm cărei funcție îi aparține punctul de tangență. Pentru a determina acest lucru, este necesar să se substituie în ecuații și să se verifice identitatea.
Exemplul 7
Scrieți o ecuație pentru tangentei la hiperbola x - 3 2 4 - y + 3 2 9 = 1 la punctul 7; - 3 3 - 3 .
Soluţie
Este necesar să se transforme înregistrarea soluției pentru găsirea unei hiperbole folosind 2 funcții. Înțelegem asta
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 și y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Este necesar să se identifice cărei funcție îi aparține un punct dat cu coordonatele 7; - 3 3 - 3 .
Evident, pentru a verifica prima funcție este necesar y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, atunci punctul nu aparține graficului, întrucât egalitatea nu se menține.
Pentru a doua funcție avem că y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, ceea ce înseamnă că punctul aparține graficului dat. De aici ar trebui să găsiți panta.
Înțelegem asta
y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Răspuns: ecuaţia tangentei poate fi reprezentată ca
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Este clar descris astfel:

Tangent la o parabolă
Pentru a crea o ecuație pentru tangenta la parabola y = a x 2 + b x + c în punctul x 0, y (x 0), trebuie să utilizați un algoritm standard, apoi ecuația va lua forma y = y "(x 0) x - x 0 + y ( x 0). O astfel de tangentă la vârf este paralelă cu x.
Ar trebui să definiți parabola x = a y 2 + b y + c ca uniunea a două funcții. Prin urmare, trebuie să rezolvăm ecuația pentru y. Înțelegem asta
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Înfățișat grafic ca:

Pentru a afla dacă un punct x 0, y (x 0) aparține unei funcții, procedați ușor conform algoritmului standard. O astfel de tangentă va fi paralelă cu o y față de parabolă.
Exemplul 8
Scrieți ecuația tangentei la graficul x - 2 y 2 - 5 y + 3 când avem un unghi de tangentă de 150 °.
Soluţie
Începem soluția reprezentând parabola ca două funcții. Înțelegem asta
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
Valoarea pantei este egală cu valoarea derivatei în punctul x 0 al acestei funcții și este egală cu tangentei unghiului de înclinare.
Primim:
k x = y „(x 0) = t g α x = t g 150 ° = - 1 3
De aici determinăm valoarea x pentru punctele de contact.
Prima funcție va fi scrisă ca
y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Evident, nu există rădăcini reale, deoarece am primit o valoare negativă. Concluzionăm că nu există o tangentă cu un unghi de 150° pentru o astfel de funcție.
A doua funcție va fi scrisă ca
y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Avem că punctele de contact sunt 23 4 ; - 5 + 3 4 .
Răspuns: ecuația tangentei ia forma
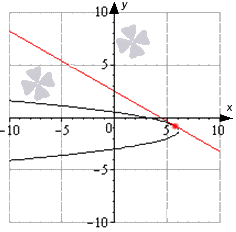
y = - 1 3 x - 23 4 + - 5 + 3 4
Să o reprezentăm grafic astfel:
Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
Tema „Coeficientul unghiular al unei tangente ca tangentă a unghiului de înclinare” are mai multe sarcini la examenul de certificare. În funcție de starea lor, absolventului i se poate cere să ofere fie un răspuns complet, fie un răspuns scurt. Când se pregătește pentru a susține examenul de stat unificat la matematică, elevul ar trebui să repete cu siguranță sarcinile care necesită calcularea pantei unei tangente.
Te va ajuta să faci asta portal educațional„Șkolkovo”. Specialiștii noștri au pregătit și au prezentat materiale teoretice și practice în cel mai accesibil mod posibil. Familiarizându-se cu acesta, absolvenții cu orice nivel de pregătire vor putea rezolva cu succes probleme legate de derivate în care este necesară găsirea tangentei unghiului tangentei.
Momente de bază
Pentru a găsi corect și decizie rațională Pentru sarcini similare din examenul de stat unificat, trebuie să vă amintiți definiția de bază: derivata reprezintă rata de schimbare a unei funcții; este egală cu tangentei unghiului tangentei trasat la graficul funcției într-un anumit punct. Este la fel de important să finalizați desenul. Vă va permite să găsiți solutie corecta Probleme la examenul de stat unificat pe derivată, în care este necesar să se calculeze tangentei unghiului tangentei. Pentru claritate, cel mai bine este să reprezentați graficul pe planul OXY.
Dacă v-ați familiarizat deja cu materialul de bază pe tema derivatelor și sunteți gata să începeți să rezolvați probleme privind calcularea tangentei unghiului tangentei, cum ar fi Teme de examen de stat unificat, puteți face acest lucru online. Pentru fiecare sarcină, de exemplu, probleme pe tema „Relația unei derivate cu viteza și accelerația unui corp”, am notat răspunsul corect și algoritmul de rezolvare. În același timp, elevii pot exersa finalizarea sarcinilor diverse niveluri dificultăți. Dacă este necesar, exercițiul poate fi salvat în secțiunea „Favorite”, astfel încât să puteți discuta mai târziu cu profesorul soluția.
Menținerea confidențialității dvs. este importantă pentru noi. Din acest motiv, am dezvoltat o Politică de confidențialitate care descrie modul în care folosim și stocăm informațiile dumneavoastră. Vă rugăm să examinați practicile noastre de confidențialitate și să ne comunicați dacă aveți întrebări.
Colectarea și utilizarea informațiilor personale
Informațiile personale se referă la date care pot fi folosite pentru a identifica sau contacta o anumită persoană.
Vi se poate cere să furnizați informațiile dumneavoastră personale în orice moment când ne contactați.
Mai jos sunt câteva exemple de tipuri de informații personale pe care le putem colecta și cum putem folosi aceste informații.
Ce informații personale colectăm:
- Când trimiteți o cerere pe site, este posibil să colectăm diverse informații, inclusiv numele, numărul de telefon, adresa dvs E-mail etc.
Cum folosim informațiile dumneavoastră personale:
- Colectat de noi Informații personale ne permite să vă contactăm și să vă informăm despre oferte unice, promoții și alte evenimente și evenimente viitoare.
- Din când în când, putem folosi informațiile dumneavoastră personale pentru a trimite notificări și comunicări importante.
- De asemenea, putem folosi informații personale în scopuri interne, cum ar fi efectuarea de audituri, analize de date și diverse cercetări pentru a îmbunătăți serviciile pe care le oferim și pentru a vă oferi recomandări cu privire la serviciile noastre.
- Dacă participați la o tragere la sorți, la un concurs sau la o promoție similară, este posibil să folosim informațiile pe care le furnizați pentru a administra astfel de programe.
Dezvăluirea informațiilor către terți
Nu dezvăluim informațiile primite de la dumneavoastră către terți.
Excepții:
- Dacă este necesar - în conformitate cu legea, procedura judiciară, procedurile judiciare și/sau în baza cererilor sau solicitărilor publice din partea agentii guvernamentale pe teritoriul Federației Ruse - dezvăluie informațiile tale personale. De asemenea, putem dezvălui informații despre dumneavoastră dacă stabilim că o astfel de dezvăluire este necesară sau adecvată pentru securitate, aplicarea legii sau alte scopuri de importanță publică.
- În cazul unei reorganizări, fuziuni sau vânzări, este posibil să transferăm informațiile personale pe care le colectăm terței părți succesoare aplicabile.
Protecția informațiilor personale
Luăm măsuri de precauție - inclusiv administrative, tehnice și fizice - pentru a vă proteja informațiile personale împotriva pierderii, furtului și utilizării greșite, precum și împotriva accesului, dezvăluirii, modificării și distrugerii neautorizate.
Respectarea vieții private la nivelul companiei
Pentru a ne asigura că informațiile dumneavoastră personale sunt în siguranță, comunicăm angajaților noștri standarde de confidențialitate și securitate și aplicăm strict practicile de confidențialitate.
În acest articol vom analiza toate tipurile de probleme de găsit
Să ne amintim sensul geometric al derivatului: dacă o tangentă este trasată la graficul unei funcții într-un punct, atunci coeficientul de pantă al tangentei (egal cu tangentei unghiului dintre tangentă și direcția pozitivă a axei) este egal cu derivata funcției la punct.


Să luăm un punct arbitrar pe tangenta cu coordonate:

Și luați în considerare un triunghi dreptunghic:

În acest triunghi 
De aici 

Aceasta este ecuația tangentei trasate la graficul funcției în punct.
Pentru a scrie ecuația tangentei, trebuie doar să cunoaștem ecuația funcției și punctul în care este trasată tangenta. Apoi putem găsi și .
Există trei tipuri principale de probleme de ecuații tangente.
1. Dat un punct de contact
2. Se dă coeficientul de pantă tangentă, adică valoarea derivatei funcției în punct.
3. Sunt date coordonatele punctului prin care se trasează tangenta, dar care nu este punctul de tangență.
Să ne uităm la fiecare tip de sarcină.
1 . Scrieți ecuația tangentei la graficul funcției ![]() la punct .
la punct .
![]() .
.
b) Aflați valoarea derivatei în punctul . Mai întâi să găsim derivata funcției
![]()
![]()
Să substituim valorile găsite în ecuația tangentei:
![]()
Să deschidem parantezele din partea dreaptă a ecuației. Primim:
Răspuns: .
2. Aflați abscisa punctelor în care funcțiile sunt tangente la grafic ![]() paralel cu axa x.
paralel cu axa x.
Dacă tangenta este paralelă cu axa x, deci unghiul dintre tangentă și direcția pozitivă a axei este zero, deci tangentea unghiului tangentei este zero. Aceasta înseamnă că valoarea derivatei funcției ![]() la punctele de contact este zero.
la punctele de contact este zero.
a) Aflați derivata funcției ![]() .
.
![]()
b) Să echivalăm derivata cu zero și să găsim valorile în care tangenta este paralelă cu axa:
![]()

Echivalând fiecare factor cu zero, obținem:
Răspuns: 0;3;5
3. Scrieți ecuații pentru tangente la graficul unei funcții , paralel Drept .
O tangentă este paralelă cu o dreaptă. Panta acestei drepte este -1. Deoarece tangentei este paralelă cu această dreaptă, prin urmare, panta tangentei este de asemenea -1. Acesta este cunoaștem panta tangentei, și, prin urmare, valoare derivată în punctul de tangență.
Acesta este al doilea tip de problemă pentru a găsi ecuația tangentei.
Deci, ni se dă funcția și valoarea derivatei în punctul de tangență.
a) Aflați punctele în care derivata funcției este egală cu -1.
Mai întâi, să găsim ecuația derivată.

Să echivalăm derivata cu numărul -1.

Să găsim valoarea funcției în punct.
![]()
(dupa conditie)
![]() .
.
b) Aflați ecuația tangentei la graficul funcției în punctul .
Să găsim valoarea funcției în punct.
![]()
(după condiție).
Să substituim aceste valori în ecuația tangentei:
![]() .
.
Răspuns:
4 . Scrieți ecuația tangentei la curbă , trecând printr-un punct
Mai întâi, să verificăm dacă punctul este un punct tangent. Dacă un punct este un punct tangent, atunci el aparține graficului funcției, iar coordonatele sale trebuie să satisfacă ecuația funcției. Să substituim coordonatele punctului în ecuația funcției.
Titlu="1sqrt(8-3^2)">. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и !} nu este un punct de contact.
Acesta este ultimul tip de problemă pentru a găsi ecuația tangentei. Primul lucru trebuie să găsim abscisa punctului tangent.
Să găsim valoarea.
Să fie punctul de contact. Punctul aparține tangentei la graficul funcției. Dacă înlocuim coordonatele acestui punct în ecuația tangentei, obținem egalitatea corectă:
 .
.
Valoarea funcției într-un punct este  .
.
Să găsim valoarea derivatei funcției în punct.
Mai întâi, să găsim derivata funcției. Acest .

Derivata intr-un punct este egala cu  .
.
Să înlocuim expresiile pentru și în ecuația tangentei. Obținem ecuația pentru:

Să rezolvăm această ecuație.
Reduceți numărătorul și numitorul fracției cu 2:

Să aducem partea dreaptă a ecuației la un numitor comun. Primim:

Să simplificăm numărătorul fracției și să înmulțim ambele părți cu - această expresie este strict mai mare decât zero.
Obținem ecuația

Să rezolvăm. Pentru a face acest lucru, să pătram ambele părți și să trecem la sistem.
Title="delim(lbrace)(matrix(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0 ) ))( )">!}
Să rezolvăm prima ecuație.
![]()
![]()
Să decidem ecuație pătratică, primim
A doua rădăcină nu îndeplinește condiția title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}
Să scriem ecuația tangentei la curbă în punct. Pentru a face acest lucru, înlocuiți valoarea în ecuație  - Am înregistrat-o deja.
- Am înregistrat-o deja.

![]()
Răspuns:
.
Instrucțiuni
Determinăm coeficientul unghiular al tangentei la curbă în punctul M.
Curba reprezentând graficul funcției y = f(x) este continuă într-o anumită vecinătate a punctului M (inclusiv punctul M însuși).
Dacă valoarea f‘(x0) nu există, atunci fie nu există tangentă, fie rulează vertical. Având în vedere acest lucru, prezența unei derivate a funcției în punctul x0 se datorează existenței unei tangente neverticale tangente la graficul funcției în punctul (x0, f(x0)). În acest caz, coeficientul unghiular al tangentei va fi egal cu f "(x0). Astfel, sensul geometric al derivatei devine clar - calculul coeficientului unghiular al tangentei.
Găsiți valoarea de abscisă a punctului tangent, care este notat cu litera „a”. Dacă coincide cu un punct tangent dat, atunci „a” va fi coordonata sa x. Determinați valoarea funcții f(a) prin substituirea în ecuație funcții valoare de abscisă.
Determinați prima derivată a ecuației funcții f’(x) și înlocuiți valoarea punctului „a”.
Lua ecuație generală tangentă, care este definită ca y = f(a) = f (a)(x – a), și înlocuiți valorile găsite ale lui a, f(a), f „(a) în ea. Ca rezultat, se va găsi soluţia graficului şi tangentei.
Rezolvați problema într-un mod diferit dacă punctul tangent dat nu coincide cu punctul tangent. În acest caz, este necesar să înlocuiți „a” în loc de numere în ecuația tangentei. După aceea, în loc de literele „x” și „y”, înlocuiți valoarea coordonatei punct dat. Rezolvați ecuația rezultată în care „a” este necunoscutul. Introduceți valoarea rezultată în ecuația tangentei.
Scrieți o ecuație pentru o tangentă cu litera „a” dacă enunțul problemei specifică ecuația funcțiiși ecuația unei drepte paralele în raport cu tangentei dorite. După aceasta avem nevoie de derivată funcții, la coordonatele din punctul „a”. Înlocuiți valoarea corespunzătoare în ecuația tangentei și rezolvați funcția.

