Curbe de ordinul doi pe un plan sunt drepte definite prin ecuații în care coordonatele variabilei XȘi y sunt cuprinse în gradul doi. Acestea includ elipsa, hiperbola și parabola.
Forma generală a ecuației curbei de ordinul doi este următoarea:
Unde A, B, C, D, E, F- numere și cel puțin unul dintre coeficienți A, B, C nu este egal cu zero.
La rezolvarea problemelor cu curbe de ordinul doi, cel mai adesea sunt luate în considerare ecuațiile canonice ale elipsei, hiperbolei și parabolei. Este ușor să treceți la ele din ecuațiile generale; exemplul 1 de probleme cu elipse îi va fi dedicat.
Elipsa data de ecuatia canonica
Definiţia an elipse. O elipsă este mulțimea tuturor punctelor planului pentru care suma distanțelor până la punctele numite focare este o valoare constantă mai mare decât distanța dintre focare.
Focalizările sunt indicate ca în figura de mai jos.
Ecuația canonică a unei elipse are forma:
Unde AȘi b (A > b) - lungimile semi-axelor, adică jumătate din lungimile segmentelor tăiate de elipsă pe axele de coordonate.
Linia dreaptă care trece prin focarele elipsei este axa ei de simetrie. O altă axă de simetrie a unei elipse este o linie dreaptă care trece prin mijlocul unui segment perpendicular pe acest segment. Punct DESPRE intersecția acestor drepte servește ca centru de simetrie al elipsei sau pur și simplu ca centru al elipsei.
Axa absciselor elipsei se intersectează în punctele ( A, DESPRE) Și (- A, DESPRE), iar axa ordonatelor este în puncte ( b, DESPRE) Și (- b, DESPRE). Aceste patru puncte sunt numite vârfuri ale elipsei. Segmentul dintre vârfurile elipsei de pe axa x se numește axa sa majoră, iar pe axa ordonatelor - axa sa minoră. Segmentele lor dinspre vârf spre centrul elipsei se numesc semi-axe.
Dacă A = b, atunci ecuația elipsei ia forma . Aceasta este ecuația unui cerc cu rază A, iar cercul este caz special elipsă. O elipsă poate fi obținută dintr-un cerc cu rază A, dacă îl comprimați în A/b ori de-a lungul axei Oi .
Exemplul 1. Verificați dacă o dreaptă dată de o ecuație generală este 
, elipsa.
Soluţie. Facem transformări ecuație generală. Folosim transferul termenului liber în partea dreaptă, împărțirea termen cu termen a ecuației cu același număr și reducerea fracțiilor:
Răspuns. Ecuația obținută în urma transformărilor este ecuația canonică a elipsei. Prin urmare, această linie este o elipsă.
Exemplul 2. Compuneți ecuația canonică a unei elipse dacă semiaxele sale sunt 5 și, respectiv, 4.
Soluţie. Ne uităm la formula pentru ecuația canonică a unei elipse și înlocuim: semiaxa majoră este A= 5, semiaxa minoră este b= 4 . Obținem ecuația canonică a elipsei:
Punctele și , indicate cu verde pe axa majoră, unde
sunt numite trucuri.
numit excentricitate elipsă.
Atitudine b/A caracterizează „oblatirea” elipsei. Cu cât acest raport este mai mic, cu atât elipsa este mai alungită de-a lungul axei majore. Cu toate acestea, gradul de alungire al unei elipse este exprimat mai des prin excentricitate, a cărei formulă este dată mai sus. Pentru diferite elipse, excentricitatea variază de la 0 la 1, rămânând întotdeauna mai mică decât unitate.
Exemplul 3. Compuneți ecuația canonică a elipsei dacă distanța dintre focare este 8 și axa majoră este 10.
Soluţie. Să tragem câteva concluzii simple:
Dacă axa majoră este egală cu 10, atunci jumătatea ei, adică semiaxa A = 5 ,
Dacă distanța dintre focare este 8, atunci numărul c dintre coordonatele focale este egală cu 4.
Inlocuim si calculam:
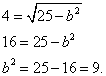
Rezultatul este ecuația canonică a elipsei:
Exemplul 4. Compuneți ecuația canonică a unei elipse dacă axa ei majoră este 26 și excentricitatea ei este .
Soluţie. După cum rezultă atât din dimensiunea axei majore, cât și din ecuația excentricității, semiaxa majoră a elipsei A= 13. Din ecuația excentricității exprimăm numărul c, necesar pentru a calcula lungimea semiaxei minore:
.
Calculăm pătratul lungimii semiaxei minore:
Compunem ecuația canonică a elipsei:
Exemplul 5. Determinați focarele elipsei date de ecuația canonică.
Soluţie. Găsiți numărul c, care determină primele coordonate ale focarelor elipsei:
.
Obținem focusurile elipsei:
Exemplul 6. Focarele elipsei sunt situate pe axă Bou simetric fata de origine. Compuneți ecuația canonică a elipsei dacă:
1) distanța dintre focusuri este 30, iar axa majoră este 34
2) axa minoră 24, iar unul dintre focusuri este în punctul (-5; 0)
3) excentricitate, iar unul dintre focare este în punctul (6; 0)
Să continuăm să rezolvăm împreună problemele elipselor
Dacă este un punct arbitrar al elipsei (indicat cu verde în partea dreaptă sus a elipsei din desen) și este distanța până la acest punct de la focare, atunci formulele pentru distanțe sunt următoarele:
Pentru fiecare punct aparținând elipsei, suma distanțelor de la focare este o valoare constantă egală cu 2 A.
Liniile definite prin ecuații
sunt numite directoare elipsă (în desen există linii roșii de-a lungul marginilor).
Din cele două ecuații de mai sus rezultă că pentru orice punct al elipsei
,
unde si sunt distantele acestui punct fata de directrice si .
Exemplul 7. Dată o elipsă. Scrieți o ecuație pentru directricele sale.
Soluţie. Ne uităm la ecuația directricei și aflăm că trebuie să găsim excentricitatea elipsei, i.e. Avem toate datele pentru asta. Noi calculăm:
.
Obținem ecuația directricelor elipsei:
Exemplul 8. Compuneți ecuația canonică a unei elipse dacă focarele sale sunt puncte și directricele sunt drepte.
Prelegeri de algebră și geometrie. Semestrul 1.
Cursul 15. Elipsa.
Capitolul 15. Elipsa.
clauza 1. Definiții de bază.
Definiție. O elipsă este GMT-ul unui plan, suma distanțelor până la două puncte fixe ale planului, numite focare, este o valoare constantă.
Definiție. Distanța de la un punct arbitrar M al planului până la focarul elipsei se numește raza focală a punctului M.
Denumiri: 
– focarele elipsei, 
– razele focale ale punctului M.
După definiția unei elipse, un punct M este un punct al unei elipse dacă și numai dacă 
– valoare constantă. Această constantă este de obicei notată ca 2a:
.
(1)
observa asta 
.
Prin definiția unei elipse, focarele sale sunt puncte fixe, deci distanța dintre ele este, de asemenea, o valoare constantă pentru o elipsă dată.
Definiție. Distanța dintre focarele elipsei se numește distanță focală.
Desemnare: 
.
Dintr-un triunghi 
urmează că 
, adică
.
Să notăm cu b numărul egal cu 
, adică
.
(2)
Definiție. Atitudine
(3)
se numește excentricitatea elipsei.
Să introducem un sistem de coordonate pe acest plan, pe care îl vom numi canonic pentru elipsă.
Definiție. Axa pe care se află focarele elipsei se numește axă focală.
Să construim un PDSC canonic pentru elipsă, vezi Fig. 2.
Selectăm axa focală ca axa absciselor și trasăm axa ordonatelor prin mijlocul segmentului 
perpendicular pe axa focală.
Apoi focarele au coordonate 
,
.
clauza 2. Ecuația canonică a unei elipse.
Teorema. În sistemul de coordonate canonic pentru o elipsă, ecuația elipsei are forma:
.
(4)
Dovada. Efectuăm dovada în două etape. În prima etapă, vom demonstra că coordonatele oricărui punct situat pe elipsă satisfac ecuația (4). În a doua etapă vom demonstra că orice soluție a ecuației (4) dă coordonatele unui punct situat pe elipsă. De aici rezultă că ecuația (4) este satisfăcută de acele și numai acele puncte ale planului de coordonate care se află pe elipsă. Din aceasta și din definiția ecuației unei curbe va rezulta că ecuația (4) este o ecuație a unei elipse.
1) Fie punctul M(x, y) un punct al elipsei, i.e. suma razelor sale focale este 2a:
.
Să folosim formula pentru distanța dintre două puncte de pe planul de coordonate și să folosim această formulă pentru a găsi razele focale ale unui punct dat M:
,
, de unde obținem:
Să mutăm o rădăcină în partea dreaptă a egalității și să o pătram:
Reducand, obtinem:
Vă prezentăm altele asemănătoare, reduceți cu 4 și îndepărtați radicalul:
.
Pătrare
Deschideți parantezele și scurtați 
:
unde ajungem:
Folosind egalitatea (2), obținem:
.
Împărțind ultima egalitate la 
, obținem egalitatea (4), etc.
2) Fie acum o pereche de numere (x, y) satisface ecuația (4) și fie M(x, y) punctul corespunzător pe planul de coordonate Oxy.
Apoi din (4) rezultă:
.
Inlocuim aceasta egalitate in expresia pentru razele focale ale punctului M:
.
Aici am folosit egalitatea (2) și (3).
Prin urmare, 
. De asemenea, 
.
Acum rețineți că din egalitatea (4) rezultă că
sau 
etc. 
, atunci inegalitatea urmează:
.
De aici rezultă, la rândul său, că
sau 
Și
,
.
(5)
Din egalităţi (5) rezultă că 
, adică punctul M(x, y) este un punct al elipsei etc.
Teorema a fost demonstrată.
Definiție. Ecuația (4) se numește ecuația canonică a elipsei.
Definiție. Axele de coordonate canonice ale unei elipse sunt numite axele principale ale elipsei.
Definiție. Originea sistemului de coordonate canonice pentru o elipsă se numește centrul elipsei.
clauza 3. Proprietățile elipsei.
Teorema. (Proprietățile unei elipse.)
1. În sistemul de coordonate canonic pentru o elipsă, totul
punctele elipsei sunt în dreptunghi
,
.
2. Punctele se află
3. O elipsă este o curbă care este simetrică în raport cu
axele lor principale.
4. Centrul elipsei este centrul ei de simetrie.
Dovada. 1, 2) Urmează imediat din ecuația canonică a elipsei.
3, 4) Fie M(x, y) un punct arbitrar al elipsei. Atunci coordonatele sale satisfac ecuația (4). Dar atunci coordonatele punctelor satisfac și ecuația (4) și, prin urmare, sunt puncte ale elipsei, din care urmează enunțurile teoremei.
Teorema a fost demonstrată.
Definiție. Mărimea 2a se numește axa majoră a elipsei, mărimea a se numește semiaxa majoră a elipsei.
Definiție. Mărimea 2b se numește axa mică a elipsei, mărimea b se numește semiaxa mică a elipsei.
Definiție. Punctele de intersecție ale unei elipse cu axele sale principale sunt numite vârfuri ale elipsei.
Cometariu. O elipsă poate fi construită după cum urmează. În avion, „locăm un cui în punctele focale” și fixăm o lungime a firului de ele 
. Apoi luăm un creion și îl folosim pentru a întinde firul. Apoi mutam mina de creion de-a lungul planului, asigurându-ne că firul este întins.
Din definiţia excentricităţii rezultă că
Să fixăm numărul a și să direcționăm numărul c la zero. Apoi la 
,
Și 
. În limita pe care o ajungem
sau 
– ecuația unui cerc.
Să ne direcționăm acum 
. Apoi 
,
si vedem ca in limita elipsa degenereaza intr-un segment de dreapta 
în notația din figura 3.
clauza 4. Ecuații parametrice ale elipsei.
Teorema. Lăsa 
– numere reale arbitrare. Apoi sistemul de ecuații
,
(6)
sunt ecuații parametrice ale unei elipse în sistemul de coordonate canonic pentru elipsă.
Dovada. Este suficient să se demonstreze că sistemul de ecuații (6) este echivalent cu ecuația (4), adică. au același set de soluții.
1) Fie (x, y) o soluție arbitrară a sistemului (6). Împărțiți prima ecuație cu a, a doua cu b, pătrați ambele ecuații și adăugați:
.
Acestea. orice soluție (x, y) a sistemului (6) satisface ecuația (4).
2) Dimpotrivă, fie perechea (x, y) o soluție a ecuației (4), adică.
.
Din această egalitate rezultă că punctul cu coordonate 
se află pe un cerc cu raza unitară cu centrul la origine, adică este un punct dintr-un cerc trigonometric căruia îi corespunde un anumit unghi 
:
Din definiția sinusului și cosinusului rezultă imediat că
,
, Unde 
, din care rezultă că perechea (x, y) este o soluție a sistemului (6), etc.
Teorema a fost demonstrată.
Cometariu. O elipsă poate fi obținută ca urmare a „compresiei” uniforme a unui cerc cu raza a spre axa absciselor.
Lăsa 
– ecuația unui cerc cu centrul la origine. „Comprimarea” unui cerc la axa absciselor nu este altceva decât o transformare a planului de coordonate, efectuată conform următoarei reguli. Pentru fiecare punct M(x, y) asociem un punct pe acelasi plan 
, Unde 
,
- rata compresiei.
Cu această transformare, fiecare punct de pe cerc „tranziție” la un alt punct din plan, care are aceeași abscisă, dar o ordonată mai mică. Să exprimăm vechea ordonată a unui punct prin cea nouă:
și înlocuiți cercuri în ecuație:
.
De aici obținem:
.
(7)
De aici rezultă că dacă înainte de transformarea „compresiei” punctul M(x, y) se afla pe cerc, i.e. coordonatele sale au satisfăcut ecuația cercului, apoi după transformarea „compresiei” acest punct s-a „transformat” în punct 
, ale cărui coordonate satisfac ecuația elipsei (7). Dacă vrem să obținem ecuația unei elipse cu axa semiminorăb, atunci trebuie să luăm factorul de compresie
.
clauza 5. Tangent la o elipsă.
Teorema. Lăsa 
– punctul arbitrar al elipsei
.
Apoi ecuația tangentei la această elipsă în punctul 
are forma:
.
(8)
Dovada. Este suficient să luăm în considerare cazul când punctul de tangență se află în primul sau al doilea sfert al planului de coordonate: 
. Ecuația elipsei din semiplanul superior are forma:
.
(9)
Să folosim ecuația tangentă la graficul funcției 
la punct 
:
Unde 
– valoarea derivatei unei funcții date într-un punct 
. Elipsa din primul trimestru poate fi considerată ca un grafic al funcției (8). Să găsim derivata și valoarea ei în punctul de tangență:
,
. Aici am profitat de faptul că punctul tangent 
este un punct al elipsei și, prin urmare, coordonatele sale satisfac ecuația elipsei (9), adică.
.
Inlocuim valoarea gasita a derivatei in ecuatia tangentei (10):
,
unde ajungem:
Asta implică:
Să împărțim această egalitate la 
:
.
Rămâne de notat că 
, deoarece punct 
aparține elipsei și coordonatele acesteia îi satisfac ecuația.
Ecuația tangentei (8) este demonstrată în mod similar în punctul de tangență situat în al treilea sau al patrulea sfert al planului de coordonate.
Și în cele din urmă, putem verifica cu ușurință că ecuația (8) dă ecuația tangentei în puncte 
,
:
sau 
, Și 
sau 
.
Teorema a fost demonstrată.
clauza 6. Proprietatea oglindă a unei elipse.
Teorema. Tangenta la elipsa are unghiuri egale cu razele focale ale punctului de tangenta.
Lăsa 
- punct de contact, 
,
– razele focale ale punctului tangent, P și Q – proiecțiile focarelor pe tangentele trasate la elipsă în punct 
.
Teorema afirmă că
.
(11)
Această egalitate poate fi interpretată ca egalitatea unghiurilor de incidență și de reflexie a unei raze de lumină dintr-o elipsă eliberată din focalizarea acesteia. Această proprietate se numește proprietatea oglindă a elipsei:
O rază de lumină eliberată din focarul elipsei, după reflectarea din oglinda elipsei, trece printr-un alt focar al elipsei.
Demonstrarea teoremei. Pentru a demonstra egalitatea unghiurilor (11), demonstrăm asemănarea triunghiurilor 
Și 
, în care părțile 
Și 
va fi similar. Deoarece triunghiurile sunt dreptunghiulare, este suficient să se demonstreze egalitatea
O elipsă este locul geometric al punctelor dintr-un plan, suma distanțelor de la fiecare dintre ele la două puncte date F_1, iar F_2 este o valoare constantă (2a) mai mare decât distanța (2c) dintre acestea. puncte date(Fig. 3.36, a). Această definiție geometrică exprimă proprietatea focală a unei elipse.
Proprietatea focală a unei elipse
Punctele F_1 și F_2 sunt numite focare ale elipsei, distanța dintre ele 2c=F_1F_2 este distanța focală, mijlocul O al segmentului F_1F_2 este centrul elipsei, numărul 2a este lungimea axei majore a elipsei. elipsa (în consecință, numărul a este semi-axa majoră a elipsei). Segmentele F_1M și F_2M care leagă un punct arbitrar M al elipsei cu focarele sale se numesc raze focale ale punctului M. Segmentul care leagă două puncte ale unei elipse se numește coardă a elipsei.
Raportul e=\frac(c)(a) se numește excentricitatea elipsei. Din definiția (2a>2c) rezultă că 0\leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
Definiția geometrică a elipsei, exprimându-și proprietatea focală, este echivalentă cu definiția sa analitică - linia dată de ecuația canonică a elipsei:
Într-adevăr, să introducem un sistem de coordonate dreptunghiular (Fig. 3.36c). Luăm centrul O al elipsei ca origine a sistemului de coordonate; luăm drept axa care trece prin focare (axa focală sau prima axă a elipsei) drept axă de abscisă (direcția pozitivă pe aceasta este de la punctul F_1 la punctul F_2); să luăm o dreaptă perpendiculară pe axa focală și care trece prin centrul elipsei (a doua axă a elipsei) ca axa ordonatelor (direcția pe axa ordonatelor este aleasă astfel încât sistemul de coordonate dreptunghiular Oxy să fie corect) .
Să creăm o ecuație pentru elipsă folosind definiția sa geometrică, care exprimă proprietatea focală. În sistemul de coordonate selectat, determinăm coordonatele focarelor F_1(-c,0),~F_2(c,0). Pentru un punct arbitrar M(x,y) aparținând elipsei, avem:
\vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a.
Scriind această egalitate sub formă de coordonate, obținem:
\sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a.
Mutăm al doilea radical în partea dreaptă, pătram ambele părți ale ecuației și aducem termeni similari:
(x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt((x-c) )^2+y^2)=4a^2-4cx.
Împărțind la 4, pătratăm ambele părți ale ecuației:
A^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2).
După ce a desemnat b=\sqrt(a^2-c^2)>0, primim b^2x^2+a^2y^2=a^2b^2. Împărțind ambele părți la a^2b^2\ne0, ajungem la ecuația canonică a elipsei:
\frac(x^2)(a^2)+\frac(y^2)(b^2)=1.
Prin urmare, sistemul de coordonate ales este canonic.
Dacă focarele elipsei coincid, atunci elipsa este un cerc (Fig. 3.36,6), deoarece a=b. În acest caz, orice sistem de coordonate dreptunghiular cu originea în punct va fi canonic O\equiv F_1\equiv F_2, iar ecuația x^2+y^2=a^2 este ecuația unui cerc cu centrul în punctul O și raza egală cu a.
Prin rationamentul in ordine inversă, se poate arăta că toate punctele ale căror coordonate satisfac ecuația (3.49), și numai ele, aparțin locului geometric al punctelor numit elipsă. Cu alte cuvinte, definiția analitică a unei elipse este echivalentă cu definiția ei geometrică, care exprimă proprietatea focală a elipsei.
Proprietatea directorială a unei elipse
Directricele unei elipse sunt două linii drepte paralele cu axa ordonatelor sistemului de coordonate canonic la aceeași distanță \frac(a^2)(c) de acesta. La c=0, când elipsa este un cerc, nu există directrice (putem presupune că directricele sunt la infinit).
Elipsa cu excentricitate 0
De fapt, de exemplu, pentru focus F_2 și directrix d_2 (Fig. 3.37,6) condiția \frac(r_2)(\rho_2)=e poate fi scris sub formă de coordonate:
\sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\right)
A scăpa de iraționalitate și a înlocui e=\frac(c)(a),~a^2-c^2=b^2, ajungem la ecuația canonică a elipsei (3.49). Raționament similar poate fi efectuat pentru focus F_1 și director d_1\colon\frac(r_1)(\rho_1)=e.
Ecuația unei elipse într-un sistem de coordonate polare
Ecuația elipsei în sistemul de coordonate polar F_1r\varphi (Fig. 3.37, c și 3.37 (2)) are forma
R=\frac(p)(1-e\cdot\cos\varphi)
unde p=\frac(b^2)(a) este parametrul focal al elipsei.
De fapt, să alegem focarul din stânga F_1 al elipsei ca pol al sistemului de coordonate polare și raza F_1F_2 ca axă polară (Fig. 3.37, c). Atunci pentru un punct arbitrar M(r,\varphi), conform definiției geometrice (proprietatea focală) a unei elipse, avem r+MF_2=2a. Exprimăm distanța dintre punctele M(r,\varphi) și F_2(2c,0) (vezi paragraful 2 din observațiile 2.8):
\begin(aligned)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(aligned)
Prin urmare, sub formă de coordonate, ecuația elipsei F_1M+F_2M=2a are forma
R+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a.
Izolăm radicalul, pătram ambele părți ale ecuației, împărțim la 4 și prezentăm termeni similari:
R^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2.
Exprimați raza polară r și faceți înlocuirea e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a):
R=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1) -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi),
Q.E.D.
Semnificația geometrică a coeficienților din ecuația elipsei
Să găsim punctele de intersecție ale elipsei (vezi Fig. 3.37a) cu axele de coordonate (vârfurile elipsei). Substituind y=0 în ecuație, găsim punctele de intersecție ale elipsei cu axa absciselor (cu axa focală): x=\pm a. Prin urmare, lungimea segmentului axei focale conținut în interiorul elipsei este egală cu 2a. Acest segment, după cum s-a menționat mai sus, este numit axa majoră a elipsei, iar numărul a este semiaxa majoră a elipsei. Înlocuind x=0, obținem y=\pm b. Prin urmare, lungimea segmentului celei de-a doua axe a elipsei conținut în interiorul elipsei este egală cu 2b. Acest segment se numește axa minoră a elipsei, iar numărul b este semiaxa minoră a elipsei.
Într-adevăr, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, iar egalitatea b=a se obține numai în cazul c=0, când elipsa este un cerc. Atitudine k=\frac(b)(a)\leqslant1 se numește raportul de compresie al elipsei.
Note 3.9
1. Dreptele x=\pm a,~y=\pm b limitează dreptunghiul principal pe planul de coordonate, în interiorul căruia se află o elipsă (vezi Fig. 3.37, a).
2. O elipsă poate fi definită ca locul punctelor obţinute prin comprimarea unui cerc până la diametrul acestuia.
Într-adevăr, fie ecuația unui cerc în sistemul de coordonate dreptunghiular Oxy x^2+y^2=a^2. Când este comprimat pe axa x cu un coeficient de 0 \begin(cases)x"=x,\\y"=k\cdot y.\end(cases) Înlocuind cercurile x=x" și y=\frac(1)(k)y" în ecuație, obținem ecuația pentru coordonatele imaginii M"(x",y") ale punctului M(x,y ) : (x")^2+(\left(\frac(1)(k)\cdot y"\right)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} întrucât b=k\cdot a . Aceasta este ecuația canonică a elipsei. 3. Axele de coordonate (ale sistemului de coordonate canonic) sunt axele de simetrie ale elipsei (numite axele principale ale elipsei), iar centrul acesteia este centrul de simetrie. Într-adevăr, dacă punctul M(x,y) aparține elipsei . atunci punctele M"(x,-y) și M""(-x,y), simetrice față de punctul M față de axele de coordonate, aparțin și ele aceleiași elipse. 4. Din ecuația elipsei din sistemul de coordonate polare r=\frac(p)(1-e\cos\varphi)(vezi Fig. 3.37, c), semnificația geometrică a parametrului focal este clarificat - aceasta este jumătate din lungimea coardei elipsei care trece prin focarul său perpendicular pe axa focală ( r = p la \varphi=\frac(\pi)(2)). 5. Excentricitatea e caracterizează forma elipsei și anume diferența dintre elipsă și cerc. Cu cât e mai mare, cu atât elipsa este mai alungită și cu cât e mai aproape de zero, cu atât elipsa este mai aproape de un cerc (Fig. 3.38a). Într-adevăr, ținând cont că e=\frac(c)(a) și c^2=a^2-b^2 , obținem E^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} unde k este factorul de compresie al elipsei, 0 6. Ecuația \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 la o
7. Ecuația \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b definește o elipsă cu centru în punctul O"(x_0,y_0), ale cărei axe sunt paralele cu axele de coordonate (Fig. 3.38, c). Această ecuație se reduce la cea canonică folosind translația paralelă (3.36). Când a=b=R ecuația (x-x_0)^2+(y-y_0)^2=R^2 descrie un cerc de raza R cu centrul în punctul O"(x_0,y_0) . Ecuația parametrică a elipseiîn sistemul de coordonate canonic are forma \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
Într-adevăr, înlocuind aceste expresii în ecuația (3.49), ajungem la identitatea trigonometrică principală \cos^2t+\sin^2t=1 . Exemplul 3.20. Desenați o elipsă \frac(x^2)(2^2)+\frac(y^2)(1^2)=1în sistemul de coordonate canonic Oxy. Găsiți semiaxele, distanța focală, excentricitatea, raportul de compresie, parametrul focal, ecuațiile directrice. Soluţie. Comparând ecuația dată cu cea canonică, determinăm semiaxele: a=2 - semiaxa majoră, b=1 - semiaxa minoră a elipsei. Construim dreptunghiul principal cu laturile 2a=4,~2b=2 cu centrul la origine (Fig. 3.39). Având în vedere simetria elipsei, o potrivim în dreptunghiul principal. Dacă este necesar, determinați coordonatele unor puncte ale elipsei. De exemplu, înlocuind x=1 în ecuația elipsei, obținem \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Prin urmare, puncte cu coordonate \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\right)- aparțin elipsei. Calcularea raportului de compresie k=\frac(b)(a)=\frac(1)(2); distanta focala 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); excentricitate e=\frac(c)(a)=\frac(\sqrt(3))(2); parametru focal p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). Compunem ecuațiile directrice: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)). O elipsă este locul geometric al punctelor dintr-un plan, suma distanțelor de la fiecare dintre acestea la două puncte date F_1, iar F_2 este o valoare constantă (2a), mai mare decât distanța (2c) dintre aceste puncte date (Fig. 3.36, a). Această definiție geometrică exprimă proprietatea focală a unei elipse. Punctele F_1 și F_2 sunt numite focare ale elipsei, distanța dintre ele 2c=F_1F_2 este distanța focală, mijlocul O al segmentului F_1F_2 este centrul elipsei, numărul 2a este lungimea axei majore a elipsei. elipsa (în consecință, numărul a este semi-axa majoră a elipsei). Segmentele F_1M și F_2M care leagă un punct arbitrar M al elipsei cu focarele sale se numesc raze focale ale punctului M. Segmentul care leagă două puncte ale unei elipse se numește coardă a elipsei. Raportul e=\frac(c)(a) se numește excentricitatea elipsei. Din definiția (2a>2c) rezultă că 0\leqslant e<1
. При e=0
, т.е. при c=0
, фокусы F_1
и F_2
, а также центр O
совпадают, и эллипс является окружностью радиуса a
(рис.3.36,6). Definiția geometrică a elipsei, exprimându-și proprietatea focală, este echivalentă cu definiția sa analitică - linia dată de ecuația canonică a elipsei: Într-adevăr, să introducem un sistem de coordonate dreptunghiular (Fig. 3.36c). Luăm centrul O al elipsei ca origine a sistemului de coordonate; luăm drept axa care trece prin focare (axa focală sau prima axă a elipsei) drept axă de abscisă (direcția pozitivă pe aceasta este de la punctul F_1 la punctul F_2); să luăm o dreaptă perpendiculară pe axa focală și care trece prin centrul elipsei (a doua axă a elipsei) ca axa ordonatelor (direcția pe axa ordonatelor este aleasă astfel încât sistemul de coordonate dreptunghiular Oxy să fie corect) . Să creăm o ecuație pentru elipsă folosind definiția sa geometrică, care exprimă proprietatea focală. În sistemul de coordonate selectat, determinăm coordonatele focarelor F_1(-c,0),~F_2(c,0). Pentru un punct arbitrar M(x,y) aparținând elipsei, avem: \vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a. Scriind această egalitate sub formă de coordonate, obținem: \sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a. Mutăm al doilea radical în partea dreaptă, pătram ambele părți ale ecuației și aducem termeni similari: (x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt((x-c) )^2+y^2)=4a^2-4cx. Împărțind la 4, pătratăm ambele părți ale ecuației: a^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2). După ce a desemnat b=\sqrt(a^2-c^2)>0, primim b^2x^2+a^2y^2=a^2b^2. Împărțind ambele părți la a^2b^2\ne0, ajungem la ecuația canonică a elipsei: \frac(x^2)(a^2)+\frac(y^2)(b^2)=1. Prin urmare, sistemul de coordonate ales este canonic. Dacă focarele elipsei coincid, atunci elipsa este un cerc (Fig. 3.36,6), deoarece a=b. În acest caz, orice sistem de coordonate dreptunghiular cu originea în punct va fi canonic O\equiv F_1\equiv F_2, iar ecuația x^2+y^2=a^2 este ecuația unui cerc cu centrul în punctul O și raza egală cu a. Efectuând raționamentul în ordine inversă, se poate demonstra că toate punctele ale căror coordonate satisfac ecuația (3.49), și numai ele, aparțin locului punctelor numit elipsă. Cu alte cuvinte, definiția analitică a unei elipse este echivalentă cu definiția ei geometrică, care exprimă proprietatea focală a elipsei. Directricele unei elipse sunt două linii drepte paralele cu axa ordonatelor sistemului de coordonate canonic la aceeași distanță \frac(a^2)(c) de acesta. La c=0, când elipsa este un cerc, nu există directrice (putem presupune că directricele sunt la infinit). Elipsa cu excentricitate 0 De fapt, de exemplu, pentru focus F_2 și directrix d_2 (Fig. 3.37,6) condiția \frac(r_2)(\rho_2)=e poate fi scris sub formă de coordonate: \sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\right) A scăpa de iraționalitate și a înlocui e=\frac(c)(a),~a^2-c^2=b^2, ajungem la ecuația canonică a elipsei (3.49). Raționament similar poate fi efectuat pentru focus F_1 și director d_1\colon\frac(r_1)(\rho_1)=e. Ecuația elipsei în sistemul de coordonate polar F_1r\varphi (Fig. 3.37, c și 3.37 (2)) are forma r=\frac(p)(1-e\cdot\cos\varphi) unde p=\frac(b^2)(a) este parametrul focal al elipsei. De fapt, să alegem focarul din stânga F_1 al elipsei ca pol al sistemului de coordonate polare și raza F_1F_2 ca axă polară (Fig. 3.37, c). Atunci pentru un punct arbitrar M(r,\varphi), conform definiției geometrice (proprietatea focală) a unei elipse, avem r+MF_2=2a. Exprimăm distanța dintre punctele M(r,\varphi) și F_2(2c,0) (vezi): \begin(aligned)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(aligned) Prin urmare, sub formă de coordonate, ecuația elipsei F_1M+F_2M=2a are forma r+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a. Izolăm radicalul, pătram ambele părți ale ecuației, împărțim la 4 și prezentăm termeni similari: r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2. Exprimați raza polară r și faceți înlocuirea e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a): r=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1 -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi), Q.E.D. Să găsim punctele de intersecție ale elipsei (vezi Fig. 3.37a) cu axele de coordonate (vârfurile elipsei). Substituind y=0 în ecuație, găsim punctele de intersecție ale elipsei cu axa absciselor (cu axa focală): x=\pm a. Prin urmare, lungimea segmentului axei focale conținut în interiorul elipsei este egală cu 2a. Acest segment, după cum s-a menționat mai sus, este numit axa majoră a elipsei, iar numărul a este semiaxa majoră a elipsei. Înlocuind x=0, obținem y=\pm b. Prin urmare, lungimea segmentului celei de-a doua axe a elipsei conținut în interiorul elipsei este egală cu 2b. Acest segment se numește axa minoră a elipsei, iar numărul b este semiaxa minoră a elipsei. Într-adevăr, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, iar egalitatea b=a se obține numai în cazul c=0, când elipsa este un cerc. Atitudine k=\frac(b)(a)\leqslant1 se numește raportul de compresie al elipsei. Note 3.9 1. Dreptele x=\pm a,~y=\pm b limitează dreptunghiul principal pe planul de coordonate, în interiorul căruia se află o elipsă (vezi Fig. 3.37, a). 2. O elipsă poate fi definită ca locul punctelor obţinute prin comprimarea unui cerc până la diametrul acestuia. Într-adevăr, fie ecuația unui cerc în sistemul de coordonate dreptunghiular Oxy x^2+y^2=a^2. Când este comprimat pe axa x cu un coeficient de 0 \begin(cases)x"=x,\\y"=k\cdot y.\end(cases) Înlocuind cercurile x=x" și y=\frac(1)(k)y" în ecuație, obținem ecuația pentru coordonatele imaginii M"(x",y") ale punctului M(x,y ) : (x")^2+(\left(\frac(1)(k)\cdot y"\right)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} întrucât b=k\cdot a . Aceasta este ecuația canonică a elipsei. 3. Axele de coordonate (ale sistemului de coordonate canonic) sunt axele de simetrie ale elipsei (numite axele principale ale elipsei), iar centrul acesteia este centrul de simetrie. Într-adevăr, dacă punctul M(x,y) aparține elipsei . atunci punctele M"(x,-y) și M""(-x,y), simetrice față de punctul M față de axele de coordonate, aparțin și ele aceleiași elipse. 4. Din ecuația elipsei din sistemul de coordonate polare r=\frac(p)(1-e\cos\varphi)(vezi Fig. 3.37, c), semnificația geometrică a parametrului focal este clarificat - aceasta este jumătate din lungimea coardei elipsei care trece prin focarul său perpendicular pe axa focală (r=p la \varphi=\frac(\pi)(2)). 5. Excentricitatea e caracterizează forma elipsei și anume diferența dintre elipsă și cerc. Cu cât e mai mare, cu atât elipsa este mai alungită și cu cât e mai aproape de zero, cu atât elipsa este mai aproape de un cerc (Fig. 3.38a). Într-adevăr, ținând cont că e=\frac(c)(a) și c^2=a^2-b^2 , obținem e^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} unde k este raportul de compresie al elipsei, 0 6. Ecuația \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 la o 7. Ecuația \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b definește o elipsă cu centru în punctul O"(x_0,y_0), ale cărei axe sunt paralele cu axele de coordonate (Fig. 3.38, c). Această ecuație se reduce la cea canonică folosind translația paralelă (3.36). Când a=b=R ecuația (x-x_0)^2+(y-y_0)^2=R^2 descrie un cerc de raza R cu centrul în punctul O"(x_0,y_0) . Ecuația parametrică a elipseiîn sistemul de coordonate canonic are forma \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
Într-adevăr, substituind aceste expresii în ecuația (3.49), ajungem la identitatea trigonometrică principală \cos^2t+\sin^2t=1. Exemplul 3.20. Desenați o elipsă \frac(x^2)(2^2)+\frac(y^2)(1^2)=1în sistemul de coordonate canonic Oxy. Găsiți semiaxele, distanța focală, excentricitatea, raportul de compresie, parametrul focal, ecuațiile directrice. Soluţie. Comparând ecuația dată cu cea canonică, determinăm semiaxele: a=2 - semiaxa majoră, b=1 - semiaxa minoră a elipsei. Construim dreptunghiul principal cu laturile 2a=4,~2b=2 cu centrul la origine (Fig. 3.39). Având în vedere simetria elipsei, o potrivim în dreptunghiul principal. Dacă este necesar, determinați coordonatele unor puncte ale elipsei. De exemplu, înlocuind x=1 în ecuația elipsei, obținem \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Prin urmare, puncte cu coordonate \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\right)- aparțin elipsei. Calcularea raportului de compresie k=\frac(b)(a)=\frac(1)(2); distanta focala 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); excentricitate e=\frac(c)(a)=\frac(\sqrt(3))(2); parametru focal p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). Compunem ecuațiile directrice: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)).Ecuația parametrică a elipsei
Pentru a efectua calcule, trebuie să activați controalele ActiveX!
Proprietatea focală a unei elipse
Proprietatea directorială a unei elipse
Ecuația unei elipse într-un sistem de coordonate polare
Semnificația geometrică a coeficienților din ecuația elipsei
Ecuația parametrică a elipsei