Una dintre cele mai importante științe, a cărei aplicare poate fi văzută în discipline precum chimia, fizica și chiar biologia, este matematica. Studierea acestei științe vă permite să dezvoltați unele calități mentale și să vă îmbunătățiți capacitatea de concentrare. Unul dintre subiectele care merită o atenție deosebită la cursul de Matematică este adunarea și scăderea fracțiilor. Mulți studenți le este greu să studieze. Poate că articolul nostru vă va ajuta să înțelegeți mai bine acest subiect.

Cum se scad fracțiile ai căror numitori sunt aceiași

Fracțiile sunt aceleași numere cu care puteți produce diverse actiuni. Diferența lor față de numerele întregi constă în prezența unui numitor. De aceea, atunci când efectuați operații cu fracții, trebuie să studiați unele dintre caracteristicile și regulile acestora. Cel mai caz simplu este scăderea fracțiilor ordinare ai căror numitori sunt reprezentați ca același număr. Efectuarea acestei acțiuni nu va fi dificilă dacă cunoașteți o regulă simplă:

• Pentru a scădea o secundă dintr-o fracție, este necesar să se scadă numărătorul fracției scăzute din numărătorul fracției care se reduce. Scriem acest număr în numărătorul diferenței și lăsăm numitorul același: k/m - b/m = (k-b)/m.

Exemple de scădere a fracțiilor ai căror numitori sunt aceiași

7/19 - 3/19 = (7 - 3)/19 = 4/19.

Din numărătorul fracției „7” scădem numărătorul fracției „3” de scăzut, obținem „4”. Scriem acest număr la numărătorul răspunsului, iar la numitor punem același număr care era în numitorii primei și celei de-a doua fracții - „19”.

Imaginea de mai jos prezintă mai multe exemple similare.

Să luăm în considerare un exemplu mai complex în care se scad fracțiile cu numitori similari:

29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7)/47 = 9/47.

Din numărătorul fracției „29” fiind redus prin scăderea pe rând a numărătorilor tuturor fracțiilor ulterioare - „3”, „8”, „2”, „7”. Drept urmare, obținem rezultatul „9”, pe care îl notăm la numărătorul răspunsului, iar la numitor notăm numărul care se află în numitorii tuturor acestor fracții - „47”.

Adunarea fracțiilor care au același numitor

Adunarea și scăderea fracțiilor obișnuite urmează același principiu.

• Pentru a adăuga fracții ai căror numitori sunt aceiași, trebuie să adăugați numărătorii. Numărul rezultat este numărătorul sumei, iar numitorul va rămâne același: k/m + b/m = (k + b)/m.

Să vedem cum arată asta folosind un exemplu:

1/4 + 2/4 = 3/4.

La numărătorul primului termen al fracției - „1” - adăugați numărătorul celui de-al doilea termen al fracției - „2”. Rezultatul - „3” - este scris în numărătorul sumei, iar numitorul rămâne același cu cel prezent în fracții - „4”.

Fracții cu numitori diferiți și scăderea lor

Am considerat deja operația cu fracții care au același numitor. După cum vedem, știind reguli simple, rezolvarea unor astfel de exemple este destul de ușoară. Dar dacă trebuie să efectuați o operație cu fracții care au numitori diferiți? Mulți elevi de liceu sunt derutați de astfel de exemple. Dar și aici, dacă cunoașteți principiul soluției, exemplele nu vă vor mai fi dificile. Există și o regulă aici, fără de care rezolvarea unor astfel de fracții este pur și simplu imposibilă.

Pentru a scădea fracții din numitori diferiti, este necesar să le reduceți la același numitor minim.



Vom vorbi mai detaliat despre cum să facem acest lucru.

Proprietatea unei fracții

Pentru a aduce mai multe fracții la același numitor, trebuie să utilizați proprietatea principală a unei fracții în soluție: după împărțirea sau înmulțirea numărătorului și numitorului cu același număr, obțineți o fracție egală cu cea dată.

Deci, de exemplu, fracția 2/3 poate avea numitori precum „6”, „9”, „12”, etc., adică poate avea forma oricărui număr care este multiplu al lui „3”. După ce înmulțim numărătorul și numitorul cu „2”, obținem fracția 4/6. După ce înmulțim numărătorul și numitorul fracției inițiale cu „3”, obținem 6/9, iar dacă facem o operație similară cu numărul „4”, obținem 8/12. O egalitate poate fi scrisă după cum urmează:

2/3 = 4/6 = 6/9 = 8/12…

Cum se transformă mai multe fracții la același numitor

Să ne uităm la cum să reducem mai multe fracții la același numitor. De exemplu, să luăm fracțiile prezentate în imaginea de mai jos. Mai întâi trebuie să determinați ce număr poate deveni numitorul pentru toate. Pentru a ușura lucrurile, să factorizăm numitorii existenți.

Numitorul fracției 1/2 și al fracției 2/3 nu pot fi factorizați. Numitorul 7/9 are doi factori 7/9 = 7/(3 x 3), numitorul fracției 5/6 = 5/(2 x 3). Acum trebuie să determinăm care factori vor fi cei mai mici pentru toate aceste patru fracții. Deoarece prima fracție are numărul „2” la numitor, înseamnă că trebuie să fie prezentă la toți numitorii; în fracția 7/9 există două triplete, ceea ce înseamnă că ambele trebuie să fie prezente și la numitor. Ținând cont de cele de mai sus, determinăm că numitorul este format din trei factori: 3, 2, 3 și este egal cu 3 x 2 x 3 = 18.



Să luăm în considerare prima fracție - 1/2. Există un „2” în numitorul său, dar nu există o singură cifră „3”, dar ar trebui să fie două. Pentru a face acest lucru, înmulțim numitorul cu două triple, dar, conform proprietății unei fracții, trebuie să înmulțim numărătorul cu două triple:
1/2 = (1 x 3 x 3)/(2 x 3 x 3) = 9/18.

Efectuăm aceleași operații cu fracțiile rămase.

• 2/3 - unul trei și unul doi lipsesc la numitor:
  2/3 = (2 x 3 x 2)/(3 x 3 x 2) = 12/18.
• 7/9 sau 7/(3 x 3) - numitorului lipsește un doi:
  7/9 = (7 x 2)/(9 x 2) = 14/18.
• 5/6 sau 5/(2 x 3) - numitorului îi lipsește un trei:
  5/6 = (5 x 3)/(6 x 3) = 15/18.

Toate împreună arată așa:



Cum să scazi și să adunăm fracții care au numitori diferiți

După cum am menționat mai sus, pentru a adăuga sau scădea fracții care au numitori diferiți, acestea trebuie reduse la același numitor, iar apoi să se folosească regulile de scădere a fracțiilor care au același numitor, care au fost deja discutate.

Să ne uităm la asta ca exemplu: 4/18 - 3/15.

Aflarea multiplului numerelor 18 și 15:

• Numărul 18 este format din 3 x 2 x 3.
• Numărul 15 este format din 5 x 3.
• Multiplu comun va fi următorii factori: 5 x 3 x 3 x 2 = 90.

După ce a fost găsit numitorul, este necesar să se calculeze factorul care va fi diferit pentru fiecare fracție, adică numărul cu care va fi necesar să se înmulțească nu numai numitorul, ci și numărătorul. Pentru a face acest lucru, împărțiți numărul pe care l-am găsit (multiplu comun) la numitorul fracției pentru care trebuie să fie determinați factori suplimentari.

• 90 împărțit la 15. Numărul rezultat „6” va fi un multiplicator pentru 3/15.
• 90 împărțit la 18. Numărul rezultat „5” va fi un multiplicator pentru 4/18.

Următoarea etapă a soluției noastre este să reducem fiecare fracție la numitorul „90”.

Am vorbit deja despre cum se face acest lucru. Să vedem cum este scris asta într-un exemplu:

(4 x 5)/(18 x 5) - (3 x 6)/(15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.

Dacă fracțiile au numere mici, atunci puteți determina numitorul comun, ca în exemplul prezentat în imaginea de mai jos.



Același lucru este valabil și pentru cei cu numitori diferiți.

Scăderea și având părți întregi

Am discutat deja în detaliu despre scăderea fracțiilor și adunarea lor. Dar cum să scadă dacă o fracție are o parte întreagă? Din nou, să folosim câteva reguli:

• Convertiți toate fracțiile care au o parte întreagă în fracții improprii. Vorbitor în cuvinte simple, scoateți întreaga parte. Pentru a face acest lucru, înmulțiți numărul părții întregi cu numitorul fracției și adăugați produsul rezultat la numărător. Numărul care iese după aceste acțiuni este numărătorul fracției improprie. Numitorul rămâne neschimbat.
• Dacă fracțiile au numitori diferiți, acestea ar trebui reduse la același numitor.
• Efectuați adunarea sau scăderea cu aceiași numitori.
• Când primiți o fracție necorespunzătoare, selectați întreaga parte.



Există un alt mod în care puteți adăuga și scădea fracții cu părți întregi. Pentru a face acest lucru, acțiunile sunt efectuate separat cu părți întregi și acțiunile cu fracții separat, iar rezultatele sunt înregistrate împreună.



Exemplul dat este format din fracții care au același numitor. În cazul în care numitorii sunt diferiți, aceștia trebuie adusi la aceeași valoare și apoi efectuați acțiunile prezentate în exemplu.

Scăderea fracțiilor din numere întregi

Un alt tip de operatie cu fractii este cazul in care o fractiune trebuie scazuta.La prima vedere, un astfel de exemplu pare greu de rezolvat. Totuși, totul este destul de simplu aici. Pentru a o rezolva, trebuie să convertiți numărul întreg într-o fracție și cu același numitor care se află în fracția scăzută. În continuare, efectuăm o scădere similară cu scăderea cu numitori identici. Într-un exemplu arată astfel:

7 - 4/9 = (7 x 9)/9 - 4/9 = 53/9 - 4/9 = 49/9.

Scăderea fracțiilor (clasa 6) prezentată în acest articol este baza pentru rezolvarea unor exemple mai complexe care sunt acoperite în notele ulterioare. Cunoașterea acestui subiect este ulterior utilizată pentru a rezolva funcții, derivate și așa mai departe. Prin urmare, este foarte important să înțelegeți și să înțelegeți operațiile cu fracții discutate mai sus.

Fracțiile sunt numere obișnuite și pot fi, de asemenea, adunate și scăzute. Dar pentru că au un numitor, necesită reguli mai complexe decât pentru numerele întregi.

Să luăm în considerare cel mai simplu caz, când există două fracții cu aceiași numitori. Apoi:

Pentru a adăuga fracții cu aceiași numitori, trebuie să adăugați numărătorii lor și să lăsați numitorul neschimbat.

Pentru a scădea fracții cu aceiași numitori, trebuie să scădeți numărătorul celui de-al doilea din numărătorul primei fracții și să lăsați din nou numitorul neschimbat.

În cadrul fiecărei expresii, numitorii fracțiilor sunt egali. Prin definiția adunării și scăderii fracțiilor obținem:

După cum puteți vedea, nu este nimic complicat: adunăm sau scădem numărătorii și gata.

Dar chiar și în așa ceva actiuni simple oamenii reușesc să facă greșeli. Ceea ce se uită cel mai adesea este că numitorul nu se schimbă. De exemplu, atunci când le adăugați, încep să se adună și acest lucru este fundamental greșit.

Scăpa de obicei prost Adăugarea numitorilor este destul de simplă. Încercați același lucru când scădeți. Ca urmare, numitorul va fi zero, iar fracția își va pierde (deodată!) sensul.

Prin urmare, amintiți-vă odată pentru totdeauna: atunci când adunați și scădeți, numitorul nu se schimbă!

Mulți oameni fac și greșeli atunci când adaugă mai multe fracții negative. Există confuzie cu semnele: unde se pune un minus și unde se pune un plus.

Această problemă este, de asemenea, foarte ușor de rezolvat. Este suficient să ne amintim că minusul dinaintea semnului unei fracții poate fi întotdeauna transferat la numărător - și invers. Și, desigur, nu uitați de două reguli simple:

1. Plus cu minus dă minus;
2. Două negative fac o afirmație.

Să ne uităm la toate acestea cu exemple specifice:

Sarcină. Găsiți sensul expresiei:

În primul caz, totul este simplu, dar în al doilea, să adăugăm minusuri la numărătorii fracțiilor:

Ce să faci dacă numitorii sunt diferiți

Nu puteți adăuga direct fracții cu numitori diferiți. Cel puțin, această metodă îmi este necunoscută. Cu toate acestea, fracțiile originale pot fi întotdeauna rescrise astfel încât numitorii să devină la fel.

Există multe modalități de a converti fracții. Trei dintre ele sunt discutate în lecția „Reducerea fracțiilor la un numitor comun”, așa că nu ne vom opri aici asupra lor. Să ne uităm la câteva exemple:

Sarcină. Găsiți sensul expresiei:

În primul caz, reducem fracțiile la un numitor comun folosind metoda „încrucișată”. În al doilea vom căuta NOC. Rețineți că 6 = 2 · 3; 9 = 3 · 3. Ultimii factori din aceste expansiuni sunt egali, iar primii sunt relativ primi. Prin urmare, LCM(6, 9) = 2 3 3 = 18.

Ce să faci dacă o fracție are o parte întreagă

Vă pot mulțumi: numitorii diferiți în fracții nu sunt cel mai mare rău. Mult mai multe erori apar atunci când întreaga parte este evidențiată în fracțiile de adunare.

Desigur, există algoritmi proprii de adunare și scădere pentru astfel de fracții, dar sunt destul de complexe și necesită un studiu lung. Utilizați mai bine diagrama simplă de mai jos:

1. Convertiți toate fracțiile care conțin o parte întreagă în fracții improprii. Obținem termeni normali (chiar cu numitori diferiți), care se calculează după regulile discutate mai sus;
2. De fapt, calculați suma sau diferența fracțiilor rezultate. Ca urmare, vom găsi practic răspunsul;
3. Dacă aceasta este tot ceea ce a fost necesar în problemă, efectuăm transformarea inversă, adică. Scăpăm de o fracție necorespunzătoare prin evidențierea întregii părți.

Regulile pentru trecerea la fracții improprii și evidențierea întregii părți sunt descrise în detaliu în lecția „Ce este o fracție numerică”. Dacă nu vă amintiți, asigurați-vă că o repetați. Exemple:

Sarcină. Găsiți sensul expresiei:

Totul este simplu aici. Numitorii din interiorul fiecărei expresii sunt egali, așa că tot ce rămâne este să convertiți toate fracțiile în fracții improprii și să numărați. Avem:

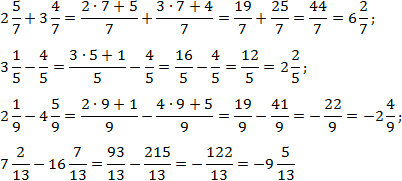
Pentru a simplifica calculele, am omis câțiva pași evidenti în ultimele exemple.

O mică notă despre ultimele două exemple, în care fracțiile cu partea întreagă evidențiată sunt scăzute. Minusul dinaintea celei de-a doua fracții înseamnă că întreaga fracție este scăzută, și nu doar întreaga sa parte.

Recitiți din nou această propoziție, uitați-vă la exemple - și gândiți-vă. Aici începătorii fac un număr mare de greșeli. Le place să dea astfel de probleme la teste. De asemenea, le veți întâlni de mai multe ori la testele pentru această lecție, care va fi publicată în curând.

Rezumat: schema generala de calcul

În concluzie, voi oferi un algoritm general care vă va ajuta să găsiți suma sau diferența a două sau mai multe fracții:

1. Dacă una sau mai multe fracții au o parte întreagă, convertiți aceste fracții în fracții improprii;
2. Aduceți toate fracțiile la un numitor comun în orice mod convenabil pentru dvs. (cu excepția cazului în care, desigur, autorii problemelor au făcut acest lucru);
3. Adunarea sau scăderea numerelor rezultate conform regulilor de adunare și scădere a fracțiilor cu numitori similari;
4. Dacă este posibil, scurtați rezultatul. Dacă fracția este incorectă, selectați întreaga parte.

Amintiți-vă că este mai bine să evidențiați întreaga parte chiar la sfârșitul sarcinii, imediat înainte de a nota răspunsul.

Acțiuni cu fracții.

Atenţie!
Există suplimentare
materiale din secțiunea specială 555.
Pentru cei care sunt foarte „nu foarte...”
Și pentru cei care „foarte mult...”)

Deci, ce sunt fracțiile, tipurile de fracții, transformările - ne-am amintit. Să trecem la problema principală.

Ce poți face cu fracțiile? Da, totul este la fel ca în cazul numerelor obișnuite. Adunați, scădeți, înmulțiți, împărțiți.

Toate aceste acțiuni cu zecimal lucrul cu fracții nu este diferit de lucrul cu numere întregi. De fapt, asta este ceea ce este bun la ei, zecimale. Singurul lucru este că trebuie să puneți virgula corect.

Numere mixte, așa cum am spus deja, sunt de puțin folos pentru majoritatea acțiunilor. Ele mai trebuie convertite în fracții obișnuite.

Dar acțiunile cu fracții obișnuite vor fi mai vicleni. Și mult mai important! Lasă-mă să-ți amintesc: toate acțiunile cu expresii fracționale cu litere, sinusuri, necunoscute și așa mai departe nu sunt diferite de acțiunile cu fracții obișnuite! Operațiile cu fracții obișnuite stau la baza tuturor algebrei. Din acest motiv vom analiza aici toată această aritmetică în detaliu.

Adunarea și scăderea fracțiilor.

Toată lumea poate adăuga (scădea) fracții cu aceiași numitori (sper foarte mult!). Ei bine, permiteți-mi să le reamintesc celor care sunt complet uituci: la adunarea (scăderea), numitorul nu se schimbă. Număratorii sunt adăugați (scădeți) pentru a da numărătorul rezultatului. Tip:

Pe scurt, în vedere generala:

Ce se întâmplă dacă numitorii sunt diferiți? Apoi, folosind proprietatea de bază a unei fracții (aici ne este util din nou!), facem numitorii la fel! De exemplu:

Aici a trebuit să facem fracția 4/10 din fracția 2/5. În scopul unic de a face numitorii la fel. Permiteți-mi să notez, pentru orice eventualitate, că 2/5 și 4/10 sunt aceeași fracție! Doar 2/5 sunt incomode pentru noi, iar 4/10 sunt chiar ok.

Apropo, aceasta este esența rezolvării oricăror probleme de matematică. Când noi din incomod facem expresii același lucru, dar mai convenabil de rezolvat.

Alt exemplu:

Situația este similară. Aici facem 48 din 16. Prin înmulțire simplă cu 3. Toate acestea sunt clare. Dar am dat peste ceva de genul:

Cum sa fii?! E greu să faci un nouă din șapte! Dar suntem deștepți, știm regulile! Să ne transformăm fiecare fracție astfel încât numitorii să fie aceiași. Aceasta se numește „reducere la un numitor comun”:

Wow! De unde am știut despre 63? Foarte simplu! 63 este un număr care este divizibil cu 7 și 9 în același timp. Un astfel de număr poate fi întotdeauna obținut prin înmulțirea numitorilor. Dacă înmulțim un număr cu 7, de exemplu, atunci rezultatul va fi cu siguranță divizibil cu 7!

Dacă trebuie să adunați (scădeți) mai multe fracții, nu este nevoie să o faceți în perechi, pas cu pas. Trebuie doar să găsiți numitorul comun tuturor fracțiilor și să reduceți fiecare fracție la același numitor. De exemplu:

Și care va fi numitorul comun? Puteți, desigur, să înmulțiți 2, 4, 8 și 16. Obținem 1024. Coșmar. Este mai ușor de estimat că numărul 16 este perfect divizibil cu 2, 4 și 8. Prin urmare, din aceste numere este ușor să obțineți 16. Acest număr va fi numitorul comun. Să transformăm 1/2 în 8/16, 3/4 în 12/16 și așa mai departe.

Apropo, dacă iei 1024 ca numitor comun, totul se va rezolva, până la urmă totul se va reduce. Dar nu toată lumea va ajunge la acest scop, din cauza calculelor...

Completați singur exemplul. Nu un fel de logaritm... Ar trebui să fie 29/16.

Deci, adunarea (scăderea) fracțiilor este clară, sper? Desigur, este mai ușor să lucrezi într-o versiune scurtată, cu multiplicatori suplimentari. Dar această plăcere este la îndemâna celor care au lucrat cinstit în clasele inferioare... Și nu au uitat nimic.

Și acum vom face aceleași acțiuni, dar nu cu fracții, ci cu expresii fracționale. O nouă greblă va fi descoperită aici, da...

Deci, trebuie să adăugăm două expresii fracționale:

Trebuie să facem numitorii la fel. Și numai cu ajutorul multiplicare! Aceasta este ceea ce dictează proprietatea principală a unei fracții. Prin urmare, nu pot adăuga unul la X în prima fracție din numitor. (ar fi drăguț!). Dar dacă înmulți numitorii, vezi, totul crește împreună! Deci notăm linia fracției, lăsăm un spațiu gol în partea de sus, apoi îl adunăm și scriem produsul numitorilor de mai jos, pentru a nu uita:

Și, desigur, nu înmulțim nimic pe partea dreaptă, nu deschidem parantezele! Și acum, privind numitorul comun din partea dreaptă, realizăm: pentru a obține numitorul x(x+1) în prima fracție, trebuie să înmulțiți numărătorul și numitorul acestei fracții cu (x+1) . Și în a doua fracție - la x. Asta este ceea ce obțineți:

Notă! Iată parantezele! Aceasta este grebla pe care calcă mulți oameni. Nu paranteze, desigur, ci absența lor. Parantezele apar pentru că ne înmulțim toate numărător și toate numitor! Și nu piesele lor individuale...

În numărătorul din dreapta scriem suma numărătorilor, totul este ca în fracții numerice, apoi deschidem parantezele în numărătorul din dreapta, adică. Înmulțim totul și dăm altele asemănătoare. Nu este nevoie să deschideți parantezele în numitori sau să înmulțiți nimic! In general, in numitori (oricare) produsul este intotdeauna mai placut! Primim:

Deci am primit răspunsul. Procesul pare lung și dificil, dar depinde de practică. Odată ce rezolvi exemplele, te obișnuiești, totul va deveni simplu. Cei care au stăpânit fracțiile la timp fac toate aceste operațiuni cu o singură mână stângă, automat!

Și încă o notă. Mulți se ocupă inteligent de fracții, dar rămân blocați cu exemple întreg numere. Cum ar fi: 2 + 1/2 + 3/4= ? Unde să fixați cele două piese? Nu trebuie să-l fixați nicăieri, trebuie să faceți o fracțiune din două. Nu este ușor, dar foarte simplu! 2=2/1. Ca aceasta. Orice număr întreg poate fi scris ca fracție. Numătorul este numărul în sine, numitorul este unul. 7 este 7/1, 3 este 3/1 și așa mai departe. La fel este și cu literele. (a+b) = (a+b)/1, x=x/1 etc. Și apoi lucrăm cu aceste fracții conform tuturor regulilor.

Ei bine, cunoștințele de adunare și scădere de fracții au fost reîmprospătate. S-a repetat conversia fracțiilor de la un tip la altul. De asemenea, puteți fi verificat. O rezolvăm puțin?)

Calculati:

Răspunsuri (în dezordine):

71/20; 3/5; 17/12; -5/4; 11/6

Înmulțirea/împărțirea fracțiilor – în lecția următoare. Există, de asemenea, sarcini pentru toate operațiunile cu fracții.

Daca va place acest site...

Apropo, mai am câteva site-uri interesante pentru tine.)

Puteți exersa rezolvarea exemplelor și puteți afla nivelul dvs. Testare cu verificare instantanee. Să învățăm - cu interes!)

Vă puteți familiariza cu funcțiile și derivatele.

Puteți efectua diverse operații cu fracții, de exemplu, adăugarea de fracții. Adunarea fracțiilor poate fi împărțită în mai multe tipuri. Fiecare tip de adunare de fracții are propriile reguli și algoritm de acțiuni. Să ne uităm la fiecare tip de adaos în detaliu.

Adunarea fracțiilor cu numitori similari.

Să ne uităm la un exemplu despre cum să adunăm fracții cu un numitor comun.

Turistii au mers in drumetie din punctul A in punctul E. In prima zi au mers de la punctul A la B sau \(\frac(1)(5)\) a intregii poteci. În a doua zi au mers de la punctul B la D sau \(\frac(2)(5)\) tot drumul. Cât de departe au călătorit de la începutul călătoriei până la punctul D?

Pentru a găsi distanța de la punctul A la punctul D, trebuie să adăugați fracțiile \(\frac(1)(5) + \frac(2)(5)\).

Adunarea fracțiilor cu numitori similari înseamnă că trebuie să adăugați numărătorii acestor fracții, dar numitorul va rămâne același.

\(\frac(1)(5) + \frac(2)(5) = \frac(1 + 2)(5) = \frac(3)(5)\)

În formă literală, suma fracțiilor cu aceiași numitori va arăta astfel:

\(\bf \frac(a)(c) + \frac(b)(c) = \frac(a + b)(c)\)

Răspuns: turiștii au mers \(\frac(3)(5)\) tot drumul.

Adunarea fracțiilor cu numitori diferiți.

Să ne uităm la un exemplu:

Trebuie să adăugați două fracții \(\frac(3)(4)\) și \(\frac(2)(7)\).

Pentru a adăuga fracții cu numitori diferiți, trebuie mai întâi să găsiți, și apoi folosiți regula pentru adunarea fracțiilor cu numitori similari.

Pentru numitorii 4 și 7, numitorul comun va fi numărul 28. Prima fracție \(\frac(3)(4)\) trebuie înmulțită cu 7. A doua fracție \(\frac(2)(7)\ ) trebuie înmulțit cu 4.

\(\frac(3)(4) + \frac(2)(7) = \frac(3 \times \color(red) (7) + 2 \times \color(red) (4))(4 \ ori \color(roșu) (7)) = \frac(21 + 8)(28) = \frac(29)(28) = 1\frac(1)(28)\)

În formă literală, obținem următoarea formulă:

\(\bf \frac(a)(b) + \frac(c)(d) = \frac(a \times d + c \times b)(b \times d)\)

Adunarea numerelor mixte sau a fracțiilor mixte.

Adunarea are loc conform legii adunării.

Pentru fracțiile mixte, adăugăm părțile întregi cu părțile întregi și părțile fracționale cu fracțiile.

Dacă părțile fracționale ale numerelor mixte au aceiași numitori, apoi adunăm numărătorii, dar numitorul rămâne același.

Să adăugăm numerele mixte \(3\frac(6)(11)\) și \(1\frac(3)(11)\).

\(3\frac(6)(11) + 1\frac(3)(11) = (\color(red) (3) + \color(blue) (\frac(6)(11))) + ( \color(red) (1) + \color(blue) (\frac(3)(11)))) = (\color(red) (3) + \color(red) (1)) + (\color( albastru) (\frac(6)(11)) + \color(blue) (\frac(3)(11))) = \color(red)(4) + (\color(blue) (\frac(6) + 3)(11))) = \color(red)(4) + \color(blue) (\frac(9)(11)) = \color(red)(4) \color(blue) (\frac (9)(11))\)

Dacă părțile fracționale ale numerelor mixte au numitori diferiți, atunci găsim numitorul comun.

Să efectuăm adunarea numerelor mixte \(7\frac(1)(8)\) și \(2\frac(1)(6)\).

Numitorul este diferit, așa că trebuie să găsim numitorul comun, acesta este egal cu 24. Înmulțiți prima fracție \(7\frac(1)(8)\) cu un factor suplimentar de 3 și a doua fracție \( 2\frac(1)(6)\) cu 4.

\(7\frac(1)(8) + 2\frac(1)(6) = 7\frac(1 \times \color(red) (3))(8 \times \color(red) (3) ) = 2\frac(1\times \color(red) (4))(6\times \color(red) (4)) =7\frac(3)(24) + 2\frac(4)(24 ) = 9\frac(7)(24)\)

Întrebări înrudite:
Cum se adună fracții?
Răspuns: mai întâi trebuie să decideți ce tip de expresie este: fracțiile au aceiași numitori, numitori diferiți sau fracții mixte. În funcție de tipul de expresie, trecem la algoritmul de soluție.

Cum se rezolvă fracții cu numitori diferiți?
Răspuns: trebuie să găsiți numitorul comun și apoi să urmați regula de adunare a fracțiilor cu aceiași numitori.

Cum se rezolvă fracțiile mixte?
Răspuns: adăugăm părți întregi cu numere întregi și părți fracționale cu fracții.

Exemplul #1:
Poate suma a două să rezulte o fracție adecvată? Fracție nepotrivită? Dă exemple.

\(\frac(2)(7) + \frac(3)(7) = \frac(2 + 3)(7) = \frac(5)(7)\)

Fracția \(\frac(5)(7)\) este o fracție proprie, este rezultatul sumei a două fracții proprii \(\frac(2)(7)\) și \(\frac(3) (7)\).

\(\frac(2)(5) + \frac(8)(9) = \frac(2 \times 9 + 8 \times 5)(5 \times 9) =\frac(18 + 40)(45) = \frac(58)(45)\)

Fracția \(\frac(58)(45)\) este o fracție improprie, este rezultatul sumei fracțiilor proprii \(\frac(2)(5)\) și \(\frac(8) (9)\).

Răspuns: Răspunsul la ambele întrebări este da.

Exemplul #2:
Adăugați fracțiile: a) \(\frac(3)(11) + \frac(5)(11)\) b) \(\frac(1)(3) + \frac(2)(9)\) .

a) \(\frac(3)(11) + \frac(5)(11) = \frac(3 + 5)(11) = \frac(8)(11)\)

b) \(\frac(1)(3) + \frac(2)(9) = \frac(1 \times \color(red) (3))(3 \times \color(red) (3)) + \frac(2)(9) = \frac(3)(9) + \frac(2)(9) = \frac(5)(9)\)

Exemplul #3:
Noteaza fracție mixtă ca suma numar naturalși fracția proprie: a) \(1\frac(9)(47)\) b) \(5\frac(1)(3)\)

a) \(1\frac(9)(47) = 1 + \frac(9)(47)\)

b) \(5\frac(1)(3) = 5 + \frac(1)(3)\)

Exemplul #4:
Calculați suma: a) \(8\frac(5)(7) + 2\frac(1)(7)\) b) \(2\frac(9)(13) + \frac(2)(13) ) \) c) \(7\frac(2)(5) + 3\frac(4)(15)\)

a) \(8\frac(5)(7) + 2\frac(1)(7) = (8 + 2) + (\frac(5)(7) + \frac(1)(7)) = 10 + \frac(6)(7) = 10\frac(6)(7)\)

b) \(2\frac(9)(13) + \frac(2)(13) = 2 + (\frac(9)(13) + \frac(2)(13)) = 2\frac(11) )(13) \)

c) \(7\frac(2)(5) + 3\frac(4)(15) = 7\frac(2\times 3)(5\times 3) + 3\frac(4)(15) = 7\frac(6)(15) + 3\frac(4)(15) = (7 + 3)+(\frac(6)(15) + \frac(4)(15)) = 10 + \frac (10)(15) = 10\frac(10)(15) = 10\frac(2)(3)\)

Sarcina 1:
La prânz am mâncat \(\frac(8)(11)\) din tort, iar seara la cină am mâncat \(\frac(3)(11)\). Crezi că tortul a fost mâncat complet sau nu?

Soluţie:
Numitorul fracției este 11, indică în câte părți a fost împărțit tortul. La prânz am mâncat 8 bucăți de tort din 11. La cină am mâncat 3 bucăți de tort din 11. Să adăugăm 8 + 3 = 11, am mâncat bucăți de tort din 11, adică tot tortul.

\(\frac(8)(11) + \frac(3)(11) = \frac(11)(11) = 1\)

Răspuns: s-a mâncat toată prăjitura.

În secolul al V-lea î.Hr., filosoful antic grec Zenon din Elea și-a formulat celebrele aporii, dintre care cea mai faimoasă este aporia „Achile și țestoasa”. Iată cum sună:

Să presupunem că Ahile aleargă de zece ori mai repede decât țestoasa și este la o mie de pași în spatele ei. În timpul necesar lui Ahile pentru a parcurge această distanță, țestoasa se va târa o sută de pași în aceeași direcție. Când Ahile aleargă o sută de pași, țestoasa se târăște încă zece pași și așa mai departe. Procesul va continua la infinit, Ahile nu va ajunge niciodată din urmă cu țestoasa.

Acest raționament a devenit un șoc logic pentru toate generațiile următoare. Aristotel, Diogene, Kant, Hegel, Hilbert... Toți au considerat într-un fel sau altul aporia lui Zenon. Șocul a fost atât de puternic încât " ...discuțiile continuă și astăzi; comunitatea științifică nu a reușit încă să ajungă la o opinie comună cu privire la esența paradoxurilor... au fost implicate în studiul problemei analiză matematică, teoria multimilor, noi abordari fizice si filozofice; niciunul dintre ele nu a devenit o soluție general acceptată la problemă...„[Wikipedia, „Aporia lui Zeno”. Toată lumea înțelege că sunt păcăliți, dar nimeni nu înțelege în ce constă înșelăciunea.

Din punct de vedere matematic, Zenon în aporia sa a demonstrat clar trecerea de la cantitate la . Această tranziție presupune aplicare în loc de cele permanente. Din câte am înțeles, aparatul matematic pentru utilizarea unităților de măsură variabile fie nu a fost încă dezvoltat, fie nu a fost aplicat aporiei lui Zeno. Aplicarea logicii noastre obișnuite ne duce într-o capcană. Noi, datorită inerției gândirii, aplicăm unități constante de timp valorii reciproce. Din punct de vedere fizic, se pare că timpul încetinește până când se oprește complet în momentul în care Ahile ajunge din urmă cu țestoasa. Dacă timpul se oprește, Ahile nu mai poate depăși țestoasa.

Dacă ne întoarcem logica obișnuită, totul cade la locul său. Ahile aleargă cu o viteză constantă. Fiecare segment ulterior al drumului său este de zece ori mai scurt decât cel anterior. În consecință, timpul petrecut pentru depășirea acestuia este de zece ori mai mic decât cel anterior. Dacă aplicăm conceptul de „infinit” în această situație, atunci ar fi corect să spunem „Achile va ajunge din urmă broasca testoasă infinit de repede”.

Cum să eviți această capcană logică? Rămâneți în unități constante de timp și nu treceți la unități reciproce. În limbajul lui Zeno arată astfel:

În timpul necesar lui Ahile să alerge o mie de pași, țestoasa se va târa o sută de pași în aceeași direcție. În următorul interval de timp egal cu primul, Ahile va alerga încă o mie de pași, iar țestoasa se va târa o sută de pași. Acum Ahile este cu opt sute de pași înaintea țestoasei.

Această abordare descrie în mod adecvat realitatea fără niciun paradox logic. Dar aceasta nu este o soluție completă a problemei. Afirmația lui Einstein despre irezistibilitatea vitezei luminii este foarte asemănătoare cu aporia lui Zeno „Achile și broasca țestoasă”. Mai trebuie să studiem, să regândim și să rezolvăm această problemă. Iar soluția trebuie căutată nu în număr infinit de mare, ci în unități de măsură.

O altă aporie interesantă a lui Zeno spune despre o săgeată zburătoare:

O săgeată zburătoare este nemișcată, deoarece în fiecare moment de timp este în repaus și, deoarece este în repaus în fiecare moment de timp, este întotdeauna în repaus.

În această aporie, paradoxul logic este depășit foarte simplu - este suficient să clarificăm că în fiecare moment de timp o săgeată zburătoare este în repaus în diferite puncte din spațiu, care, de fapt, este mișcare. Un alt punct trebuie remarcat aici. Dintr-o fotografie a unei mașini de pe șosea este imposibil să se determine nici faptul mișcării acesteia, fie distanța până la ea. Pentru a determina dacă o mașină se mișcă, aveți nevoie de două fotografii făcute din același punct în momente diferite, dar nu puteți determina distanța față de ele. Pentru a determina distanța până la o mașină, aveți nevoie de două fotografii făcute din diferite puncte ale spațiului la un moment dat, dar din ele nu puteți determina faptul mișcării (desigur, mai aveți nevoie de date suplimentare pentru calcule, trigonometria vă va ajuta ). Ce vreau să subliniez Atentie speciala, este că două puncte în timp și două puncte în spațiu sunt lucruri diferite care nu trebuie confundate, deoarece oferă oportunități diferite pentru cercetare.

miercuri, 4 iulie 2018

Diferențele dintre set și multiset sunt descrise foarte bine pe Wikipedia. Să vedem.

După cum puteți vedea, „nu pot exista două elemente identice într-o mulțime”, dar dacă există elemente identice într-o mulțime, un astfel de set se numește „multiset”. Ființele rezonabile nu vor înțelege niciodată o asemenea logică absurdă. Acesta este nivelul papagalilor vorbitori și al maimuțelor dresate, care nu au inteligență din cuvântul „complet”. Matematicienii acționează ca formatori obișnuiți, propovăduindu-ne ideile lor absurde.

Pe vremuri, inginerii care au construit podul se aflau într-o barcă sub pod în timp ce testau podul. Dacă podul s-a prăbușit, inginerul mediocru a murit sub dărâmăturile creației sale. Dacă podul putea rezista la sarcină, talentatul inginer a construit alte poduri.

Indiferent de cât de matematicieni se ascund în spatele expresiei „amintește-mă, sunt în casă” sau, mai degrabă, „matematica studiază concepte abstracte”, există un cordon ombilical care le conectează inextricabil cu realitatea. Acest cordon ombilical este bani. Aplicabil teorie matematică seturi către matematicienii înșiși.

Am studiat foarte bine matematica și acum stăm la casa de marcat, dăm salarii. Deci un matematician vine la noi pentru banii lui. Îi numărăm întreaga sumă și o întindem pe masa noastră în grămezi diferite, în care punem bancnote de aceeași valoare. Apoi luăm o bancnotă din fiecare grămadă și îi dăm matematicianului „setul său matematic de salariu”. Să-i explicăm matematicianului că va primi bancnotele rămase doar atunci când va dovedi că o mulțime fără elemente identice nu este egală cu o mulțime cu elemente identice. Aici începe distracția.

În primul rând, logica deputaților va funcționa: „Acest lucru poate fi aplicat altora, dar nu și mie!” Apoi vor începe să ne liniștească că bancnotele de aceeași denominație au numere de bancnote diferite, ceea ce înseamnă că nu pot fi considerate aceleași elemente. Bine, să numărăm salariile în monede - nu există numere pe monede. Aici matematicianul va începe să-și amintească frenetic de fizică: pe diferite monede există cantități diferite murdăria, structura cristalină și aranjamentul atomic al fiecărei monede sunt unice...

Și acum am cel mai mult interes Întreabă: unde este linia dincolo de care elementele unui multiset se transforma in elemente ale unei multimi si invers? O astfel de linie nu există - totul este hotărât de șamani, știința nu este nici măcar aproape să zacă aici.

Uite aici. Selectăm stadioane de fotbal cu aceeași suprafață de teren. Zonele câmpurilor sunt aceleași - ceea ce înseamnă că avem un multiset. Dar dacă ne uităm la numele acestor stadioane, obținem multe, pentru că numele sunt diferite. După cum puteți vedea, același set de elemente este atât un set, cât și un multiset. Care este corect? Și aici matematicianul-șamanul-ascuțitor scoate un as de atuuri din mânecă și începe să ne vorbească fie despre un set, fie despre un multiset. În orice caz, ne va convinge că are dreptate.

Pentru a înțelege cum funcționează șamanii moderni cu teoria mulțimilor, legând-o de realitate, este suficient să răspundem la o întrebare: prin ce diferă elementele unui set de elementele altui set? Vă voi arăta, fără niciun „conceput ca nu un singur întreg” sau „neconceput ca un singur întreg”.

Duminică, 18 martie 2018

Suma cifrelor unui număr este un dans al șamanilor cu o tamburină, care nu are nimic de-a face cu matematica. Da, la lecțiile de matematică suntem învățați să găsim suma cifrelor unui număr și să o folosim, dar de aceea ei sunt șamani, pentru a-și învăța descendenții abilitățile și înțelepciunea, altfel șamanii pur și simplu vor muri.

Ai nevoie de dovezi? Deschideți Wikipedia și încercați să găsiți pagina „Suma cifrelor unui număr”. Ea nu există. Nu există nicio formulă în matematică care să poată fi folosită pentru a găsi suma cifrelor oricărui număr. La urma urmei, cifrele sunt simboluri grafice, cu ajutorul căruia scriem numere și în limbajul matematicii sarcina sună astfel: „Găsiți suma simbolurilor grafice care reprezintă orice număr”. Matematicienii nu pot rezolva această problemă, dar șamanii o pot face cu ușurință.

Să ne dăm seama ce și cum facem pentru a găsi suma cifrelor unui număr dat. Și așa, să avem numărul 12345. Ce trebuie făcut pentru a găsi suma cifrelor acestui număr? Să luăm în considerare toți pașii în ordine.

1. Notează numărul pe o foaie de hârtie. Ce am făcut? Am convertit numărul într-un simbol numeric grafic. Aceasta nu este o operație matematică.

2. Tăiem o imagine rezultată în mai multe imagini care conțin numere individuale. Decuparea unei imagini nu este o operație matematică.

3. Convertiți simbolurile grafice individuale în numere. Aceasta nu este o operație matematică.

4. Adăugați numerele rezultate. Acum asta e matematica.

Suma cifrelor numărului 12345 este 15. Acestea sunt „cursurile de tăiere și cusut” predate de șamani pe care le folosesc matematicienii. Dar asta nu este tot.

Din punct de vedere matematic, nu contează în ce sistem de numere scriem un număr. Deci, în sisteme de numere diferite, suma cifrelor aceluiași număr va fi diferită. În matematică, sistemul numeric este indicat ca indice în dreapta numărului. CU un numar mare 12345 Nu vreau să-mi păcălesc capul, să ne uităm la numărul 26 din articolul despre . Să scriem acest număr în sisteme de numere binar, octal, zecimal și hexazecimal. Nu ne vom uita la fiecare pas la microscop; am făcut-o deja. Să ne uităm la rezultat.

După cum puteți vedea, în sisteme numerice diferite, suma cifrelor aceluiași număr este diferită. Acest rezultat nu are nimic de-a face cu matematica. Este la fel ca și cum ai determina aria unui dreptunghi în metri și centimetri, ai obține rezultate complet diferite.

Zero arată la fel în toate sistemele de numere și nu are sumă de cifre. Acesta este un alt argument în favoarea faptului că. Întrebare pentru matematicieni: cum este ceva care nu este un număr desemnat în matematică? Ce, pentru matematicieni nu există nimic în afară de numere? Pot permite asta șamanilor, dar nu și oamenilor de știință. Realitatea nu este doar despre cifre.

Rezultatul obținut ar trebui considerat ca o dovadă că sistemele numerice sunt unități de măsură pentru numere. La urma urmei, nu putem compara numerele cu unități de măsură diferite. Dacă aceleaşi acţiuni cu unităţi de măsură diferite ale aceleiaşi mărimi conduc la rezultate diferite după ce le comparăm, înseamnă că nu are nicio legătură cu matematica.

Ce este matematica reală? Acesta este momentul în care rezultatul unei operații matematice nu depinde de mărimea numărului, de unitatea de măsură folosită și de cine efectuează această acțiune.

Semnează pe uşă El deschide ușa și spune:

Oh! Asta nu este toaleta pentru femei?
- Femeie tânără! Acesta este un laborator pentru studiul sfințeniei nefilice a sufletelor în timpul înălțării lor la cer! Halo în partea de sus și săgeată în sus. Ce altă toaletă?

Femeie... Aureola de sus și săgeata în jos sunt masculine.

Dacă o astfel de operă de artă de design îți fulgerează în fața ochilor de mai multe ori pe zi,

Atunci nu este surprinzător că găsiți brusc o pictogramă ciudată în mașina dvs.:

Personal, fac un efort să văd minus patru grade la o persoană care face caca (o poză) (o compoziție din mai multe imagini: un semn minus, numărul patru, o denumire de grade). Și nu cred că această fată este o proastă care nu știe fizică. Ea are doar un stereotip puternic de a percepe imaginile grafice. Și matematicienii ne învață asta tot timpul. Iată un exemplu.

1A nu este „minus patru grade” sau „unu a”. Acesta este „pooping om” sau numărul „douăzeci și șase” în notație hexazecimală. Acei oameni care lucrează constant în acest sistem numeric percep automat un număr și o literă ca un simbol grafic.