În ultima lecție, am învățat cum să adunăm și să scădem zecimale (vezi lecția „Adunarea și scăderea zecimalelor”). În același timp, am evaluat cât de mult calculele sunt simplificate în comparație cu fracțiile obișnuite „cu două etaje”.
Din păcate, cu înmulțirea și împărțirea zecimale nu apare un astfel de efect. În unele cazuri, notația zecimală chiar complică aceste operații.
Mai întâi, să introducem o nouă definiție. Îl vom vedea destul de des, și nu doar în această lecție.
Partea semnificativă a unui număr este tot ce se află între prima și ultima cifră diferită de zero, inclusiv capete. Este despre numai despre numere, punctul zecimal nu este luat în considerare.
Numerele incluse în parte semnificativă numerele se numesc cifre semnificative. Ele pot fi repetate și chiar egale cu zero.
De exemplu, luați în considerare câteva fracții zecimale și scrieți părțile semnificative corespunzătoare:
- 91,25 → 9125 (cifre semnificative: 9; 1; 2; 5);
- 0,008241 → 8241 (cifre semnificative: 8; 2; 4; 1);
- 15,0075 → 150075 (cifre semnificative: 1; 5; 0; 0; 7; 5);
- 0,0304 → 304 (cifre semnificative: 3; 0; 4);
- 3000 → 3 (există o singură cifră semnificativă: 3).
Vă rugăm să rețineți: zerourile din interiorul părții semnificative a numărului nu merg nicăieri. Am întâlnit deja ceva similar când am învățat să convertim fracțiile zecimale în fracții obișnuite (vezi lecția „Decimale”).
Acest punct este atât de important și aici se fac greșeli atât de des, încât în viitorul apropiat voi publica un test pe această temă. Asigurați-vă că exersați! Și noi, înarmați cu conceptul părții semnificative, vom trece, de fapt, la subiectul lecției.
Înmulțirea zecimalelor
Operația de înmulțire constă din trei etape succesive:
- Pentru fiecare fracție, notați partea semnificativă. Veți obține două numere întregi obișnuite - fără numitori și puncte zecimale;
- Înmulțiți aceste numere în orice mod convenabil. Direct, dacă numerele sunt mici, sau într-o coloană. Obținem partea semnificativă a fracției dorite;
- Aflați unde și cu câte cifre este deplasată punctul zecimal din fracțiile originale pentru a obține partea semnificativă corespunzătoare. Efectuați schimburi inverse pentru partea semnificativă obținută în pasul anterior.
Permiteți-mi să vă reamintesc încă o dată că zerourile de pe părțile laterale ale părții semnificative nu sunt niciodată luate în considerare. Ignorarea acestei reguli duce la erori.
- 0,28 12,5;
- 6,3 · 1,08;
- 132,5 · 0,0034;
- 0,0108 1600,5;
- 5,25 · 10.000.
Se lucrează cu prima expresie: 0,28 · 12,5.
- Să notăm părțile semnificative pentru numerele din această expresie: 28 și 125;
- Produsul lor: 28 · 125 = 3500;
- În primul factor punctul zecimal este deplasat cu 2 cifre la dreapta (0,28 → 28), iar în al doilea este deplasat cu încă 1 cifră. În total, aveți nevoie de o deplasare la stânga cu trei cifre: 3500 → 3.500 = 3,5.
Acum să ne uităm la expresia 6.3 · 1.08.
- Să scriem părțile semnificative: 63 și 108;
- Produsul lor: 63 · 108 = 6804;
- Din nou, două deplasări la dreapta: cu 2 și, respectiv, 1 cifră. Total - din nou 3 cifre la dreapta, deci schimbarea inversă va fi de 3 cifre la stânga: 6804 → 6.804. De data aceasta, nu există zerouri finale.
Am ajuns la a treia expresie: 132,5 · 0,0034.
- Părți semnificative: 1325 și 34;
- Produsul lor: 1325 · 34 = 45.050;
- În prima fracțiune, punctul zecimal se deplasează la dreapta cu 1 cifră, iar în a doua - cu până la 4. Total: 5 la dreapta. Ne deplasăm cu 5 la stânga: 45.050 → .45050 = 0.4505. Zeroul a fost eliminat la sfârșit și adăugat în față pentru a nu lăsa un punct zecimal „gol”.
Următoarea expresie este: 0,0108 · 1600,5.
- Scriem părțile semnificative: 108 și 16 005;
- Le înmulțim: 108 · 16.005 = 1.728.540;
- Numărăm numerele după virgulă: în primul număr sunt 4, în al doilea sunt 1. Totalul este din nou 5. Avem: 1.728.540 → 17,28540 = 17,2854. La final, zeroul „extra” a fost eliminat.
În sfârșit, ultima expresie: 5,25 10.000.
- Părți semnificative: 525 și 1;
- Le înmulțim: 525 · 1 = 525;
- Prima fracție este deplasată cu 2 cifre la dreapta, iar a doua fracție este deplasată cu 4 cifre la stânga (10.000 → 1,0000 = 1). Total 4 − 2 = 2 cifre la stânga. Efectuăm o deplasare inversă cu 2 cifre la dreapta: 525, → 52.500 (a trebuit să adăugăm zerouri).
Rețineți în ultimul exemplu: deoarece punctul zecimal se mișcă în direcții diferite, deplasarea totală se găsește prin diferență. Aceasta este foarte punct important! Iată un alt exemplu:
Se consideră numerele 1,5 și 12 500. Avem: 1,5 → 15 (deplasare cu 1 la dreapta); 12.500 → 125 (deplasarea 2 la stânga). „Pașim” cu 1 cifră la dreapta și apoi 2 la stânga. Ca rezultat, am făcut pasul 2 − 1 = 1 cifră spre stânga.
Împărțire zecimală
Diviziunea este poate cea mai dificilă operațiune. Desigur, aici puteți acționa prin analogie cu înmulțirea: împărțiți părțile semnificative și apoi „mutați” punctul zecimal. Dar în acest caz există multe subtilități care anulează potențialele economii.
Prin urmare, să ne uităm la un algoritm universal, care este puțin mai lung, dar mult mai fiabil:
- Convertiți toate fracțiile zecimale în fracții obișnuite. Cu puțină practică, acest pas vă va dura câteva secunde;
- Împărțiți fracțiile rezultate în mod clasic. Cu alte cuvinte, înmulțiți prima fracție cu a doua „inversată” (vezi lecția „Înmulțirea și împărțirea fracțiilor numerice”);
- Dacă este posibil, prezentați din nou rezultatul ca o fracție zecimală. Acest pas este, de asemenea, rapid, deoarece numitorul este adesea deja o putere a zece.
Sarcină. Găsiți sensul expresiei:
- 3,51: 3,9;
- 1,47: 2,1;
- 6,4: 25,6:
- 0,0425: 2,5;
- 0,25: 0,002.
Să luăm în considerare prima expresie. Mai întâi, să convertim fracțiile în zecimale:
Să facem același lucru cu a doua expresie. Numătorul primei fracții va fi din nou factorizat:
Există un punct important în al treilea și al patrulea exemplu: după ce scăpați de notația zecimală, apar fracțiile reductibile. Cu toate acestea, nu vom efectua această reducere.
Ultimul exemplu este interesant deoarece numărătorul celei de-a doua fracții conține un număr prim. Pur și simplu nu este nimic de factorizat aici, așa că o luăm în considerare direct:
Uneori, împărțirea are ca rezultat un număr întreg (vorbesc despre ultimul exemplu). În acest caz, al treilea pas nu este efectuat deloc.
În plus, la împărțire, apar adesea fracții „urâte” care nu pot fi convertite în zecimale. Acest lucru distinge împărțirea de înmulțire, unde rezultatele sunt întotdeauna reprezentate în formă zecimală. Desigur, în acest caz, ultimul pas nu este din nou efectuat.
Acordați atenție și celui de-al 3-lea și al 4-lea exemple. În ele, nu reducem în mod deliberat fracțiile obișnuite obținute din zecimale. În caz contrar, acest lucru va complica sarcina inversă - reprezentând răspunsul final din nou în formă zecimală.
Amintiți-vă: proprietatea de bază a unei fracții (ca orice altă regulă din matematică) în sine nu înseamnă că trebuie aplicată peste tot și întotdeauna, cu orice ocazie.
eu. Pentru a împărți o fracție zecimală la numar natural, trebuie să împărțiți fracția la acest număr, pe măsură ce împărțiți numerele naturale și să puneți o virgulă în coeficient atunci când împărțirea întregii părți este finalizată.
Exemple.
Efectuați împărțirea: 1) 96,25: 5; 2) 4,78: 4; 3) 183,06: 45.
Soluţie.
Exemplu 1) 96,25: 5.
Împărțim cu un „colț” în același mod în care sunt împărțite numerele naturale. După ce luăm numărul 2 (numărul de zecimi este prima cifră după virgulă din dividendul 96, 2 5), în coeficient punem virgulă și continuăm împărțirea.
Răspuns: 19,25.
Exemplu 2) 4,78: 4.
Împărțim pe măsură ce numerele naturale sunt împărțite. În coeficient vom pune o virgulă imediat ce o scoatem 7
— prima cifră după virgulă din dividendul 4, 7
8. Continuăm împărțirea mai departe. La scăderea 38-36 obținem 2, dar împărțirea nu este finalizată. Cum procedăm? Știm că zerouri pot fi adăugate la sfârșitul unei fracții zecimale - acest lucru nu va schimba valoarea fracției. Atribuim zero și împărțim 20 la 4. Obținem 5 - împărțirea s-a terminat.
Răspuns: 1,195.
Exemplu 3) 183,06: 45.
Împărțiți ca 18306 la 45. În coeficient punem o virgulă imediat ce eliminăm numărul 0
— prima cifră după virgulă din dividendul 183, 0
6. La fel ca în exemplul 2), a trebuit să atribuim zero numărului 36 - diferența dintre numerele 306 și 270.
Răspuns: 4,068.
Concluzie: la împărțirea unei fracții zecimale la un număr natural în privat punem virgulă imediat după ce luăm în jos cifra de pe locul zecimii al dividendului. Vă rugăm să rețineți: toate evidențiate numere în roșu în aceste trei exemple aparţin categoriei zecimi din dividend.
II. Pentru a împărți o fracție zecimală la 10, 100, 1000 etc., trebuie să mutați punctul zecimal la stânga cu 1, 2, 3, etc. cifre.
Exemple.
Efectuați împărțirea: 1) 41,56: 10; 2) 123,45: 100; 3) 0,47: 100; 4) 8,5: 1000; 5) 631,2: 10000.
Soluţie.
Mutarea punctului zecimal la stânga depinde de câte zerouri sunt după unu în divizor. Deci, atunci când împărțiți o fracție zecimală la 10
vom reporta în dividend virgulă la o cifră din stânga; când se împarte la 100
- muta virgula stânga două cifre; când se împarte la 1000
convertiți în această fracție zecimală virgulă trei cifre la stânga.
În acest articol ne vom uita la o operație atât de importantă cu zecimale precum împărțirea. Mai întâi să formulăm principii generale, apoi ne vom uita la cum să împărțim corect fracțiile zecimale pe coloane atât cu alte fracții, cât și după numere naturale. În continuare, vom analiza împărțirea fracțiilor obișnuite în zecimale și invers, iar la sfârșit ne vom uita la modul de împărțire corectă a fracțiilor care se termină în 0, 1, 0, 01, 100, 10 etc.
Aici vom lua doar cazurile cu fracții pozitive. Dacă există un minus în fața fracției, atunci pentru a opera cu el trebuie să studiați materiale despre împărțirea numerelor raționale și reale.
Yandex.RTB R-A-339285-1
Toate fracțiile zecimale, atât finite, cât și periodice, sunt doar o formă specială de scriere a fracțiilor obișnuite. Prin urmare, ele sunt supuse acelorași principii ca și fracțiile lor ordinare corespunzătoare. Astfel, reducem întregul proces de împărțire a fracțiilor zecimale la înlocuirea lor cu unele obișnuite, urmat de calcul folosind metode deja cunoscute nouă. Să luăm un exemplu concret.
Exemplul 1
Împărțiți 1,2 la 0,48.
Soluţie
Să scriem fracții zecimale ca fracții obișnuite. Vom obține:
1 , 2 = 12 10 = 6 5
0 , 48 = 48 100 = 12 25 .
Astfel, trebuie să împărțim 6 5 la 12 25. Numaram:
1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2
Din rezultatul fracție improprie puteți selecta întreaga parte și obțineți număr mixt 2 1 2, sau o puteți reprezenta ca o fracție zecimală, astfel încât să corespundă numerelor originale: 5 2 = 2, 5. Am scris deja despre cum să facem acest lucru mai devreme.
Răspuns: 1 , 2: 0 , 48 = 2 , 5 .
Exemplul 2
Calculați cât va fi 0 , (504) 0 , 56.
Soluţie
În primul rând, trebuie să convertim o fracție zecimală periodică într-o fracție comună.
0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111
După aceasta, vom converti și fracția zecimală finală într-o altă formă: 0, 56 = 56.100. Acum avem două numere cu care ne va fi ușor să efectuăm calculele necesare:
0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 100 56 = 100 111
Avem un rezultat pe care îl putem converti și în formă zecimală. Pentru a face acest lucru, împărțiți numărătorul la numitor folosind metoda coloanei:
Răspuns: 0 , (504) : 0 , 56 = 0 , (900) .
Dacă în exemplul de împărțire am întâlnit fracții zecimale neperiodice, atunci vom acționa puțin diferit. Nu le putem reduce la fracțiile obișnuite, așa că atunci când împărțim trebuie mai întâi să le rotunjim la o anumită cifră. Această acțiune trebuie efectuată atât cu dividendul, cât și cu divizorul: vom rotunji și fracția finită sau periodică existentă în interesul acurateții.
Exemplul 3
Aflați cât este 0,779... / 1,5602.
Soluţie
Mai întâi, rotunjim ambele fracții la cea mai apropiată sutime. Iată cum trecem de la fracții neperiodice infinite la fracții zecimale finite:
0 , 779 … ≈ 0 , 78
1 , 5602 ≈ 1 , 56
Putem continua calculele și obținem un rezultat aproximativ: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78.100: 156.100 = 78.100 100.156 = 78.156 = 1 2 = 0.
Precizia rezultatului va depinde de gradul de rotunjire.
Răspuns: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .
Cum se împarte un număr natural cu o zecimală și invers
Abordarea împărțirii în acest caz este aproape aceeași: înlocuim fracțiile finite și periodice cu unele obișnuite și le rotunjim pe cele neperiodice infinite. Să începem cu exemplul împărțirii cu un număr natural și o fracție zecimală.
Exemplul 4
Împărțiți 2,5 la 45.
Soluţie
Să reducem 2, 5 la forma unei fracții ordinare: 255 10 = 51 2. În continuare trebuie doar să-l împărțim la un număr natural. Știm deja cum să facem asta:
25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30
Dacă convertim rezultatul în notație zecimală, obținem 0,5 (6).
Răspuns: 25 , 5: 45 = 0 , 5 (6) .
Metoda împărțirii lungi este bună nu numai pentru numerele naturale. Prin analogie, îl putem folosi pentru fracții. Mai jos indicăm succesiunea de acțiuni care trebuie efectuate pentru aceasta.
Definiția 1
Pentru a împărți o coloană de fracții zecimale la numere naturale aveți nevoie de:
1. Adăugați câteva zerouri la fracția zecimală din dreapta (pentru împărțire putem adăuga orice număr dintre ele de care avem nevoie).
2. Împărțiți o fracție zecimală la un număr natural folosind un algoritm. Când împărțirea întregii părți a fracției se termină, punem o virgulă în coeficientul rezultat și numărăm în continuare.
Rezultatul unei astfel de împărțiri poate fi o fracție zecimală periodică finită sau infinită. Depinde de rest: dacă este zero, atunci rezultatul va fi finit, iar dacă restul încep să se repete, atunci răspunsul va fi o fracție periodică.
Să luăm ca exemplu câteva probleme și să încercăm să efectuăm acești pași cu numere specifice.
Exemplul 5
Calculați cât va fi 65, 14 4.
Soluţie
Folosim metoda coloanei. Pentru a face acest lucru, adăugați două zerouri la fracție și obțineți fracția zecimală 65, 1400, care va fi egală cu cea inițială. Acum scriem o coloană pentru împărțirea la 4:
Numărul rezultat va fi rezultatul de care avem nevoie de la împărțirea părții întregi. Punem o virgulă, separând-o și continuăm:
Am ajuns la zero rest, prin urmare procesul de împărțire este complet.
Răspuns: 65 , 14: 4 = 16 , 285 .
Exemplul 6
Împărțiți 164,5 la 27.
Soluţie
Mai întâi împărțim partea fracțională și obținem:
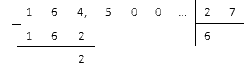
Separați numărul rezultat cu o virgulă și continuați împărțirea:
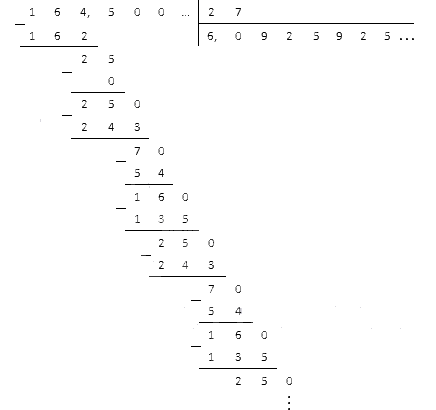
Vedem că resturile au început să se repete periodic, iar în coeficient numerele nouă, doi și cinci au început să se alterneze. Ne vom opri aici și vom scrie răspunsul sub forma unei fracții periodice 6, 0 (925).
Răspuns: 164 , 5: 27 = 6 , 0 (925) .
Această împărțire poate fi redusă la procesul de găsire a câtului dintre o fracție zecimală și un număr natural, deja descris mai sus. Pentru a face acest lucru, trebuie să înmulțim dividendul și divizorul cu 10, 100 etc., astfel încât divizorul să se transforme într-un număr natural. În continuare, efectuăm secvența de acțiuni descrisă mai sus. Această abordare este posibilă datorită proprietăților împărțirii și înmulțirii. Le-am notat astfel:
a: b = (a · 10) : (b · 10) , a: b = (a · 100) : (b · 100) și așa mai departe.
Să formulăm o regulă:
Definiția 2
Pentru a împărți o fracție zecimală finală la alta:
1. Mutați virgula în dividend și divizor la dreapta cu numărul de cifre necesar pentru a transforma divizorul într-un număr natural. Dacă nu există suficiente semne în dividend, îi adăugăm zerouri în partea dreaptă.
2. După aceasta, împărțiți fracția la o coloană la numărul natural rezultat.
Să ne uităm la o problemă specifică.
Exemplul 7
Împărțiți 7,287 la 2,1.
Soluție: Pentru a face din divizor un număr natural, trebuie să mutăm zecimala cu un loc la dreapta. Așa că am trecut la împărțirea fracției zecimale 72, 87 la 21. Să scriem numerele rezultate într-o coloană și să calculăm
Răspuns: 7 , 287: 2 , 1 = 3 , 47
Exemplul 8
Calculați 16.30.021.
Soluţie
Va trebui să mutăm virgula cu trei locuri. Nu există suficiente cifre în divizor pentru aceasta, ceea ce înseamnă că trebuie să utilizați zerouri suplimentare. Credem că rezultatul va fi:
Vedem repetarea periodică a reziduurilor 4, 19, 1, 10, 16, 13. În coeficient, 1, 9, 0, 4, 7 și 5 se repetă. Atunci rezultatul nostru este fracția zecimală periodică 776, (190476).
Răspuns: 16 , 3: 0 , 021 = 776 , (190476)
Metoda pe care am descris-o vă permite să faceți opusul, adică să împărțiți un număr natural la fracția zecimală finală. Să vedem cum se face.
Exemplul 9
Calculați cât este 3 5, 4.
Soluţie
Evident, va trebui să mutăm virgula în locul potrivit. După aceasta, putem trece la împărțirea 30, 0 la 54. Să scriem datele într-o coloană și să calculăm rezultatul:
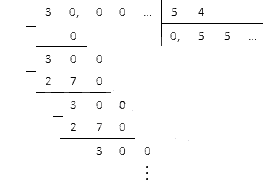
Repetând restul ne dă numărul final 0, (5), care este o fracție zecimală periodică.
Răspuns: 3: 5 , 4 = 0 , (5) .
Cum se împarte zecimale la 1000, 100, 10 etc.
Conform regulilor deja studiate pentru împărțirea fracțiilor obișnuite, împărțirea unei fracții la zeci, sute, mii este similară cu înmulțirea ei cu 1/1000, 1/100, 1/10 etc. Se dovedește că pentru a efectua împărțirea, în în acest caz este suficient să mutați pur și simplu punctul zecimal la cantitatea necesară numere Dacă nu există suficiente valori în numărul de transferat, trebuie să adăugați numărul necesar de zerouri.
Exemplul 10
Deci, 56, 21: 10 = 5, 621 și 0, 32: 100.000 = 0, 0000032.
În cazul fracțiilor zecimale infinite, procedăm la fel.
Exemplul 11
De exemplu, 3, (56): 1.000 = 0, 003 (56) și 593, 374...: 100 = 5, 93374....
Cum se împarte zecimale la 0,001, 0,01, 0,1 etc.
Folosind aceeași regulă, putem împărți și fracții în valorile indicate. Această acțiune va fi similară cu înmulțirea cu 1000, 100, respectiv 10. Pentru a face acest lucru, mutăm virgula la una, două sau trei cifre, în funcție de condițiile problemei, și adăugăm zerouri dacă nu există suficiente cifre în număr.
Exemplul 12
De exemplu, 5,739: 0,1 = 57,39 și 0,21: 0,00001 = 21.000.
Această regulă se aplică și fracțiilor zecimale infinite. Vă sfătuim doar să aveți grijă la perioada fracției care apare în răspuns.
Deci, 7, 5 (716) : 0, 01 = 757, (167) pentru că după ce am mutat virgula în fracția zecimală 7, 5716716716... două locuri la dreapta, am primit 757, 167167....
Dacă avem fracții neperiodice în exemplu, atunci totul este mai simplu: 394, 38283...: 0, 001 = 394382, 83....
Cum se împarte un număr sau o fracție mixtă cu o zecimală și invers
De asemenea, reducem această acțiune la operațiuni cu fracții obișnuite. Pentru a face acest lucru, trebuie să înlocuiți numere zecimale fracțiile ordinare corespunzătoare și scrieți numărul mixt ca fracție improprie.
Dacă împărțim o fracție neperiodică la un număr obișnuit sau mixt, trebuie să facem invers, înlocuind fracție comună sau un număr mixt cu fracția zecimală corespunzătoare.
Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
Să ne uităm la exemple de împărțire a zecimalelor în această lumină.
Exemplu.
Împărțiți fracția zecimală 1,2 la fracția zecimală 0,48.
Soluţie.
Răspuns:
1,2:0,48=2,5 .
Exemplu.
Împărțiți fracția zecimală periodică 0.(504) la fracția zecimală 0.56.
Soluţie.
Să transformăm fracția zecimală periodică într-o fracție obișnuită: . De asemenea, convertim fracția zecimală finală 0,56 într-o fracție obișnuită, avem 0,56 = 56/100. Acum putem trece de la împărțirea zecimalelor inițiale la împărțirea fracțiilor obișnuite și să încheiem calculele: .
Să convertim fracția obișnuită rezultată într-o fracție zecimală, împărțind numărătorul la numitorul cu o coloană:
Răspuns:
0,(504):0,56=0,(900) .
Principiul împărțirii fracțiilor zecimale neperiodice infinite diferă de principiul împărțirii fracțiilor zecimale finite și periodice, deoarece fracțiile zecimale neperiodice nu pot fi convertite în fracții obișnuite. Împărțirea fracțiilor zecimale infinite neperiodice se reduce la împărțirea fracțiilor zecimale finite, pentru care efectuăm rotunjirea numerelor până la un anumit nivel. Mai mult, dacă unul dintre numerele cu care se realizează împărțirea este o fracție zecimală finită sau periodică, atunci se rotunjește și la aceeași cifră ca și fracția zecimală neperiodică.
Exemplu.
Împărțiți zecimala infinită neperiodică 0,779... la zecimala finită 1,5602.
Soluţie.
Mai întâi trebuie să rotunjiți zecimale, astfel încât să puteți trece de la împărțirea infinitelor zecimale neperiodice la împărțirea zecimale finite. Putem rotunji la cea mai apropiată sutime: 0,779…≈0,78 și 1,5602≈1,56. Astfel, 0,779…:1,5602≈0,78:1,56= 78/100:156/100=78/100·100/156= 78/156=1/2=0,5 .
Răspuns:
0,779…:1,5602≈0,5 .
Împărțirea unui număr natural la o fracție zecimală și invers
Esența abordării împărțirii unui număr natural la o fracție zecimală și a împărțirii unei fracții zecimale la un număr natural nu este diferită de esența împărțirii fracțiilor zecimale. Adică, fracțiile finite și periodice sunt înlocuite cu fracții obișnuite, iar fracțiile neperiodice infinite sunt rotunjite.
Pentru a ilustra, luați în considerare exemplul împărțirii unei fracții zecimale la un număr natural.
Exemplu.
Împărțiți fracția zecimală 25,5 la numărul natural 45.
Soluţie.
Prin înlocuirea fracției zecimale 25,5 cu fracția comună 255/10=51/2, împărțirea se reduce la împărțirea fracției comune la un număr natural:. Fracția rezultată în notație zecimală are forma 0,5(6) .
Răspuns:
25,5:45=0,5(6) .
Împărțirea unei fracții zecimale la un număr natural cu o coloană
Este convenabil să împărțiți fracțiile zecimale finite în numere naturale printr-o coloană, prin analogie cu împărțirea printr-o coloană de numere naturale. Să prezentăm regula împărțirii.
La împărțiți o fracție zecimală la un număr natural folosind o coloană, necesar:
- adăugați mai multe cifre 0 la dreapta fracției zecimale care este împărțită (în timpul procesului de împărțire, dacă este necesar, puteți adăuga orice număr de zerouri, dar este posibil ca aceste zerouri să nu fie necesare);
- efectuați împărțirea printr-o coloană a unei fracții zecimale cu un număr natural conform tuturor regulilor de împărțire a unei coloane de numere naturale, dar când împărțirea întregii părți a fracției zecimale este finalizată, atunci în coeficient trebuie să puneți o virgulă și continuă împărțirea.
Să spunem imediat că, ca rezultat al împărțirii unei fracții zecimale finite la un număr natural, puteți obține fie o fracție zecimală finită, fie o fracție zecimală periodică infinită. Într-adevăr, după ce împărțirea tuturor zecimale non-0 este finalizată fracție divizibilă, fie restul poate fi 0 și vom obține o fracție zecimală finală, fie resturile vor începe să se repete periodic și vom obține o fracție zecimală periodică.
Să înțelegem toate complexitățile împărțirii fracțiilor zecimale la numere naturale într-o coloană atunci când rezolvăm exemple.
Exemplu.
Împărțiți fracția zecimală 65,14 la 4.
Soluţie.
Să împărțim o fracție zecimală la un număr natural folosind o coloană. Să adăugăm câteva zerouri la dreapta în notația fracției 65,14 și vom obține o fracție zecimală egală 65,1400 (vezi fracțiile zecimale egale și inegale). Acum puteți începe să împărțiți cu o coloană partea întreagă a fracției zecimale 65,1400 la numărul natural 4: 
Aceasta completează împărțirea părții întregi a fracției zecimale. Aici, în coeficient, trebuie să puneți un punct zecimal și să continuați împărțirea: 
Am ajuns la un rest de 0, în această etapă se termină împărțirea după coloană. Ca rezultat, avem 65.14:4=16.285.
Răspuns:
65,14:4=16,285 .
Exemplu.
Împărțiți 164,5 la 27.
Soluţie.
Să împărțim fracția zecimală la un număr natural folosind o coloană. După împărțirea întregii părți obținem următoarea imagine: 
Acum punem o virgulă în coeficient și continuăm împărțirea cu o coloană: 
Acum este clar că reziduurile 25, 7 și 16 au început să se repete, în timp ce în coeficient se repetă numerele 9, 2 și 5. Astfel, împărțirea zecimalei 164,5 la 27 ne dă zecimala periodică 6,0(925) .
Răspuns:
164,5:27=6,0(925) .
Împărțirea pe coloane a fracțiilor zecimale
Împărțirea unei fracții zecimale cu o fracție zecimală poate fi redusă la împărțirea unei fracții zecimale la un număr natural cu o coloană. Pentru a face acest lucru, dividendul și divizorul trebuie înmulțite cu un număr precum 10, sau 100, sau 1.000 etc., astfel încât divizorul să devină un număr natural și apoi împărțit cu un număr natural cu o coloană. Putem face acest lucru datorită proprietăților împărțirii și înmulțirii, deoarece a:b=(a·10):(b·10) , a:b=(a·100):(b·100) și așa mai departe.
Cu alte cuvinte, pentru a împărți o zecimală finală la o zecimală finală, trebuie sa:
- în dividend și divizor, mutați virgula la dreapta cu câte locuri există după punctul zecimal din divizor; dacă în dividend nu există suficiente semne pentru a muta virgula, atunci trebuie să adăugați numărul necesar de zerouri la dreapta;
- După aceasta, împărțiți cu o coloană zecimală la un număr natural.
Când rezolvați un exemplu, luați în considerare aplicarea acestei reguli de împărțire cu o fracție zecimală.
Exemplu.
Împărțiți cu o coloană 7,287 la 2,1.
Soluţie.
Să mutăm virgula în aceste fracții zecimale cu o cifră la dreapta, acest lucru ne va permite să trecem de la împărțirea fracției zecimale 7,287 la fracția zecimală 2,1 la împărțirea fracției zecimale 72,87 la numărul natural 21. Să facem împărțirea după coloană: 
Răspuns:
7,287:2,1=3,47 .
Exemplu.
Împărțiți zecimala 16,3 la zecimala 0,021.
Soluţie.
Mutați virgula în dividend și divizor în cele trei locuri din dreapta. Evident, divizorul nu are suficiente cifre pentru a muta punctul zecimal, așa că vom adăuga numărul necesar de zerouri la dreapta. Acum să împărțim fracția 16300.0 cu o coloană la numărul natural 21: 
Din acest moment, resturile 4, 19, 1, 10, 16 si 13 incep sa se repete, ceea ce inseamna ca se vor repeta si numerele 1, 9, 0, 4, 7 si 6 din cat. Ca rezultat, obținem fracția zecimală periodică 776,(190476) .
Răspuns:
16,3:0,021=776,(190476) .
Rețineți că regula anunțată vă permite să împărțiți un număr natural cu o coloană într-o fracție zecimală finală.
Exemplu.
Împărțiți numărul natural 3 la fracția zecimală 5.4.
Soluţie.
După ce am mutat virgulă zecimală cu o cifră la dreapta, ajungem la împărțirea numărului 30,0 la 54. Să facem împărțirea după coloană: 
.
Această regulă se poate aplica și la împărțirea fracțiilor zecimale infinite la 10, 100, .... De exemplu, 3,(56):1,000=0,003(56) și 593,374…:100=5,93374… .
Împărțirea zecimalelor la 0,1, 0,01, 0,001 etc.
Deoarece 0,1 = 1/10, 0,01 = 1/100 etc., atunci din regula împărțirii la o fracție comună rezultă că se împarte fracția zecimală la 0,1, 0,01, 0,001 etc. este același lucru cu înmulțirea unei date zecimale cu 10, 100, 1.000 etc. respectiv.
Cu alte cuvinte, pentru a împărți o fracție zecimală la 0,1, 0,01, ... trebuie să mutați punctul zecimal la dreapta cu 1, 2, 3, ... cifre, iar dacă cifrele din fracția zecimală nu sunt suficiente pentru a muta punctul zecimal, atunci trebuie să adăugați numărul necesar la zerourile din dreapta.
De exemplu, 5.739:0.1=57.39 și 0.21:0.00001=21.000.
Aceeași regulă poate fi aplicată la împărțirea fracțiilor zecimale infinite la 0,1, 0,01, 0,001 etc. În acest caz, ar trebui să fii foarte atent la împărțirea fracțiilor periodice pentru a nu greși cu perioada fracției care se obține ca urmare a împărțirii. De exemplu, 7.5(716):0.01=757,(167), deoarece după mutarea punctului zecimal în fracția zecimală 7.5716716716... două locuri la dreapta, avem intrarea 757.167167.... Cu fracții zecimale neperiodice infinite totul este mai simplu: 394,38283…:0,001=394382,83… .
Împărțirea unei fracții sau a unui număr mixt cu o zecimală și invers
Împărțirea unei fracții comune sau număr mixt la o fracție zecimală finită sau periodică, precum și împărțirea unei fracții zecimale finite sau periodice la o fracție comună sau număr mixt, se reduce la împărțirea fracțiilor comune. Pentru a face acest lucru, fracțiile zecimale sunt înlocuite cu fracțiile ordinare corespunzătoare, iar numărul mixt este reprezentat ca o fracție improprie.
Când împărțiți o fracție zecimală neperiodică infinită la o fracție comună sau un număr mixt și invers, ar trebui să treceți la împărțirea fracțiilor zecimale, înlocuind fracția comună sau numărul mixt cu fracția zecimală corespunzătoare.
Bibliografie.
- Matematică: manual pentru clasa a 5-a. educatie generala instituții / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - Ed. 21, șters. - M.: Mnemosyne, 2007. - 280 p.: ill. ISBN 5-346-00699-0.
- Matematică. Clasa a VI-a: educațională. pentru învăţământul general instituții / [N. Ya. Vilenkin și alții]. - Ed. a 22-a, rev. - M.: Mnemosyne, 2008. - 288 p.: ill. ISBN 978-5-346-00897-2.
- Algebră: manual pentru clasa a VIII-a. educatie generala instituții / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; editat de S. A. Teliakovsky. - Ed. a XVI-a. - M.: Educație, 2008. - 271 p. : bolnav. - ISBN 978-5-09-019243-9.
- Gusev V. A., Mordkovich A. G. Matematică (un manual pentru cei care intră în școlile tehnice): Proc. indemnizatie.- M.; Superior şcoală, 1984.-351 p., ill.
Să notăm regula și să luăm în considerare aplicarea ei folosind exemple.
Când împărțiți o fracție zecimală la un număr natural:
1) împărțiți fără să acordați atenție virgulei;
2) când se termină împărțirea întregii părți, punem virgulă în coeficient.
Dacă întreaga parte mai mic decât divizorul, atunci partea întreagă a coeficientului este egală cu zero.
Exemple de împărțire a fracțiilor zecimale la numere naturale.
Împărțim fără să fim atenți la virgulă, adică împărțim 348 la 6. Când împărțim 34 la 6, luăm fiecare câte 5. 5∙6=30, 34-30=4, adică restul este 4.
Diferența dintre împărțirea unei fracții zecimale la un număr natural și împărțirea numerelor întregi este doar că, atunci când împărțirea părții întregi este finalizată, punem o virgulă în coeficient. Adică, când trecem printr-o virgulă, înainte de a o coborî la restul împărțirii părții întregi, 4, numărul 8 din partea fracțională, scriem o virgulă în coeficient.
Luăm jos 8. 48:6=8. In privat scriem 8.
Deci, 34,8:6=5,8.
Deoarece 5 nu este divizibil cu 12, scriem zero în coeficient. Împărțirea întregii părți este finalizată, punem virgulă în coeficient.
Luăm 1. Când împărțim 51 la 12, luăm 4. Restul este 3.
Luăm jos 6. 36:12=3.
Astfel, 5,16:12=0,43.
3) 0,646:38=?
Partea întreagă a dividendului conține zero. Întrucât zero nu este divizibil cu 38, punem în cât 0. Împărțirea părții întregi este finalizată, în cât se scrie virgulă.
Luăm 6. Deoarece 6 nu este divizibil cu 38, mai scriem un zero în cât.
Luăm 4. Când împărțim 64 la 38, luăm 1. Restul este 26.
Luăm jos 6. 266:38=7.
Deci, 0,646:38=0,017.
4) 14917,5:325=?
Când împărțim 1491 la 325, luăm fiecare 4. Restul este 191. Luăm 7. Când împărțim 1917 la 325, luăm fiecare 5. Restul este 292.
Deoarece împărțirea întregii părți este finalizată, scriem o virgulă în coeficient.