Cu matricea A, dacă există un număr l astfel încât AX = lX.

În acest caz, numărul l se numește valoarea proprie a operatorului (matricea A), corespunzătoare vectorului X.

Cu alte cuvinte, un vector propriu este un vector care, sub acțiunea unui operator liniar, se transformă într-un vector coliniar, i.e. doar înmulțiți cu un anumit număr. În schimb, vectorii nepotriviți sunt mai complex de transformat.

Să notăm definiția unui vector propriu sub forma unui sistem de ecuații:

Să mutăm toți termenii în partea stângă:

Ultimul sistem poate fi scris sub formă de matrice după cum urmează:

(A - lE)X = O

Sistemul rezultat are întotdeauna o soluție zero X = O. Astfel de sisteme în care toți termenii liberi sunt egali cu zero se numesc omogene. Dacă matricea unui astfel de sistem este pătrată și determinantul său nu este egal cu zero, atunci folosind formulele lui Cramer vom obține întotdeauna o soluție unică - zero. Se poate dovedi că un sistem are soluții diferite de zero dacă și numai dacă determinantul acestei matrice este egal cu zero, adică.

|A - lE| = = 0

Această ecuație cu l necunoscut se numește ecuația caracteristică (polinom caracteristic) a matricei A (operatorul liniar).

Se poate dovedi că polinomul caracteristic al unui operator liniar nu depinde de alegerea bazei.

De exemplu, să găsim valorile proprii și vectorii proprii ai operatorului liniar definit de matricea A = .

Pentru a face acest lucru, să creăm o ecuație caracteristică |A - lE| = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; valori proprii l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.

Pentru a găsi vectori proprii, rezolvăm două sisteme de ecuații

(A + 5E)X = O

(A - 7E)X = O

Pentru prima dintre ele, matricea extinsă ia forma

,

de unde x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, adică. X (1) = (-(2/3)s; s).

Pentru al doilea dintre ele, matricea extinsă ia forma

,

de unde x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, adică X (2) = ((2/3)s 1; s 1).

Astfel, vectorii proprii ai acestui operator liniar sunt toți vectorii de forma (-(2/3)с; с) cu valoare proprie (-5) și toți vectorii de forma ((2/3)с 1 ; с 1) cu valoare proprie 7 .

Se poate dovedi că matricea operatorului A în baza formată din vectorii săi proprii este diagonală și are forma:

,

unde l i sunt valorile proprii ale acestei matrice.

Este adevărat și invers: dacă matricea A într-o anumită bază este diagonală, atunci toți vectorii acestei baze vor fi vectori proprii ai acestei matrice.

Se poate dovedi, de asemenea, că dacă un operator liniar are n valori proprii distincte pe perechi, atunci vectorii proprii corespunzători sunt independenți liniar, iar matricea acestui operator în baza corespunzătoare are o formă diagonală.

Să ilustrăm acest lucru cu exemplul anterior. Să luăm valori arbitrare diferite de zero c și c 1, dar astfel încât vectorii X (1) și X (2) sunt independenți liniar, adică. ar constitui o bază. De exemplu, fie c = c 1 = 3, apoi X (1) = (-2; 3), X (2) = (2; 3).

Să verificăm independența liniară a acestor vectori:

12 ≠ 0. În această nouă bază, matricea A va lua forma A * = .

Pentru a verifica acest lucru, să folosim formula A * = C -1 AC. Mai întâi, să găsim C -1.

C -1 = ;

Forme pătratice

Forma pătratică f(x 1, x 2, x n) a n variabile este o sumă, fiecare termen fiind fie pătratul uneia dintre variabile, fie produsul a două variabile diferite, luate cu un anumit coeficient: f( x 1, x 2, x n ) = (a ij = a ji).

Matricea A compusă din acești coeficienți se numește matrice de formă pătratică. Aceasta este întotdeauna o matrice simetrică (adică o matrice simetrică față de diagonala principală, a ij = a ji).

În notația matriceală, forma pătratică este f(X) = X T AX, unde

Într-adevăr

De exemplu, să scriem forma pătratică sub formă de matrice.

Pentru a face acest lucru, găsim o matrice de formă pătratică. Elementele sale diagonale sunt egale cu coeficienții variabilelor pătrate, iar elementele rămase sunt egale cu jumătățile coeficienților corespunzători formei pătratice. De aceea

Fie coloana-matrice a variabilelor X obținută printr-o transformare liniară nedegenerată a coloanei-matrice Y, adică. X = CY, unde C este o matrice nesingulară de ordin al n-lea. Atunci forma pătratică f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Astfel, cu o transformare liniară nedegenerată C, matricea de formă pătratică ia forma: A * = C T AC.

De exemplu, să găsim forma pătratică f(y 1, y 2), obţinută din forma pătratică f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 prin transformare liniară.

O formă pătratică se numește canonică (are o formă canonică) dacă toți coeficienții ei a ij = 0 pentru i ≠ j, adică.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .

Matricea sa este diagonală.

Teoremă (dovada nu este dată aici). Orice formă pătratică poate fi redusă la formă canonică folosind o transformare liniară nedegenerată.

De exemplu, să reducem forma pătratică la forma canonică
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Pentru a face acest lucru, mai întâi selectați un pătrat complet cu variabila x 1:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Acum selectăm un pătrat complet cu variabila x 2:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2.

Atunci transformarea liniară nedegenerată y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 și y 3 = x 3 aduce această formă pătratică la forma canonică f(y 1, y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Rețineți că forma canonică a unei forme pătratice este determinată în mod ambiguu (aceeași formă pătratică poate fi redusă la forma canonică căi diferite). Cu toate acestea, cele primite căi diferite formele canonice au un număr de proprietăți generale. În special, numărul de termeni cu coeficienți pozitivi (negativi) ai unei forme pătratice nu depinde de metoda de reducere a formei la această formă (de exemplu, în exemplul luat în considerare vor exista întotdeauna doi coeficienti negativi și unul pozitiv). Această proprietate se numește legea inerției formelor pătratice.

Să verificăm acest lucru prin aducerea aceleiași forme pătratice la forma canonică într-un mod diferit. Să începem transformarea cu variabila x 2:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, unde y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 și y 3 = x 1 . Aici există un coeficient negativ -3 la y 1 și doi coeficienți pozitivi 3 și 2 la y 2 și y 3 (și folosind o altă metodă am obținut un coeficient negativ (-5) la y 2 și doi pozitivi: 2 la y 1 și 1/20 la y 3).

De asemenea, trebuie remarcat faptul că rangul unei matrice de formă pătratică, numit rangul formei pătratice, este egal cu numărul de coeficienți nenuli ai formei canonice și nu se modifică în cazul transformărilor liniare.

O formă pătratică f(X) se numește pozitivă (negativă) definită dacă pentru toate valorile variabilelor care nu sunt simultan egale cu zero, este pozitivă, adică. f(X) > 0 (negativ, adică
f(X)< 0).

De exemplu, forma pătratică f 1 (X) = x 1 2 + x 2 2 este definită pozitiv, deoarece este o sumă de pătrate, iar forma pătratică f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 este definită negativă, deoarece îl reprezintă poate fi reprezentat ca f 2 (X) = -(x 1 - x 2) 2.

In majoritate situatii practice Este ceva mai dificil de stabilit semnul definit al unei forme pătratice, așa că pentru aceasta folosim una dintre următoarele teoreme (le vom formula fără dovezi).

Teorema. O formă pătratică este pozitivă (negativă) definită dacă și numai dacă toate valorile proprii ale matricei sale sunt pozitive (negative).

Teorema (criteriul Sylvester). O formă pătratică este pozitivă definită dacă și numai dacă toate principalele minore ale matricei acestei forme sunt pozitive.

Principalul (unghiular) minor al ordinului k al matricei A de ordinul n este determinantul matricei, compus din primele k rânduri și coloane ale matricei A ().

Rețineți că pentru formele pătratice definite negative semnele minorilor principali alternează, iar minorul de ordinul întâi trebuie să fie negativ.

De exemplu, să examinăm forma pătratică f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 pentru definiția semnului.

= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
. Prin urmare, forma pătratică este definită pozitivă.

Metoda 2. Minor principal de ordinul I al matricei A D 1 = a 11 = 2 > 0. Minor principal de ordinul II D 2 = = 6 - 4 = 2 > 0. Prin urmare, conform criteriului lui Sylvester, forma patratică este definit pozitiv.

Examinăm o altă formă pătratică pentru definiția semnului, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metoda 1. Să construim o matrice de formă pătratică A = . Ecuație caracteristică va arăta ca = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Prin urmare, forma pătratică este definită negativă.

Metoda 2. Minor principal de ordinul I al matricei A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. În consecință, după criteriul lui Sylvester, forma pătratică este definită negativă (semnele principalelor minori alternează, începând cu minus).

Și ca un alt exemplu, examinăm forma pătratică determinată de semn f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metoda 1. Să construim o matrice de formă pătratică A = . Ecuația caracteristică va avea forma = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Unul dintre aceste numere este negativ, iar celălalt este pozitiv. Semnele valorilor proprii sunt diferite. În consecință, forma pătratică nu poate fi definită nici negativ, nici pozitiv, adică. această formă pătratică nu este definită de semn (poate lua valori ale oricărui semn).

Metoda 2. Minor principal de ordinul I al matricei A D 1 = a 11 = 2 > 0. Minor principal de ordinul II D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

SISTEM DE ECUAȚII LINEARE OMogene

Sistem de omogen ecuatii lineare numit un sistem al formei

Este clar că în acest caz , deoarece toate elementele uneia dintre coloanele din acești determinanți sunt egale cu zero.

Întrucât necunoscutele se găsesc după formule , atunci în cazul în care Δ ≠ 0, sistemul are o soluție unică zero X = y = z= 0. Cu toate acestea, în multe probleme întrebarea interesantă este dacă sistem omogen alte soluții decât zero.

Teorema. Pentru sistemul liniar ecuații omogene a avut o soluție diferită de zero, este necesar și suficient ca Δ ≠ 0.

Deci, dacă determinantul Δ ≠ 0, atunci sistemul are o soluție unică. Dacă Δ ≠ 0, atunci sistemul de ecuații liniare omogene are set infinit decizii.

Exemple.

Vectorii proprii și valorile proprii ale unei matrice

Să fie dat matrice pătrată , X– o coloană-matrice a cărei înălțime coincide cu ordinea matricei A. .

În multe probleme trebuie să luăm în considerare ecuația pt X

unde λ este un anumit număr. Este clar că pentru orice λ această ecuație are o soluție zero.

Se numește numărul λ pentru care această ecuație are soluții diferite de zero valoare proprie matrici A, A X căci astfel de λ se numește vector propriu matrici A.

Să găsim vectorul propriu al matricei A. Deoarece E∙X = X, atunci ecuația matriceală poate fi rescrisă ca sau . În formă extinsă, această ecuație poate fi rescrisă ca un sistem de ecuații liniare. Într-adevăr .

Prin urmare

Deci, am obținut un sistem de ecuații liniare omogene pentru determinarea coordonatelor x 1, x 2, x 3 vector X. Pentru ca un sistem să aibă soluții diferite de zero este necesar și suficient ca determinantul sistemului să fie egal cu zero, i.e.

Aceasta este o ecuație de gradul 3 pentru λ. Se numeste ecuație caracteristică matrici Ași servește la determinarea valorilor proprii ale lui λ.

Fiecare valoare proprie λ corespunde unui vector propriu X, ale căror coordonate sunt determinate din sistem la valoarea corespunzătoare a lui λ.

Exemple.

ALGEBRA VECTORALĂ. CONCEPTUL DE VECTOR

Când se studiază diferite ramuri ale fizicii, există cantități care sunt complet determinate prin specificarea valorilor lor numerice, de exemplu, lungimea, suprafața, masa, temperatura etc. Astfel de mărimi se numesc scalare. Cu toate acestea, pe lângă ele, există și cantități, pentru a determina care, pe lângă valoarea numerică, este necesar să se cunoască și direcția lor în spațiu, de exemplu, forța care acționează asupra corpului, viteza și accelerația corpul atunci când se mișcă în spațiu, puterea câmpului magnetic într-un anumit punct din spațiu și etc. Astfel de mărimi se numesc mărimi vectoriale.

Să introducem o definiție strictă.

Segment regizat Să numim un segment, relativ la capete ale căruia se știe care dintre ele este primul și care este al doilea.

Vector numit segment direcționat având o anumită lungime, adică Acesta este un segment de o anumită lungime, în care unul dintre punctele care îl limitează este luat drept început, iar al doilea ca sfârșit. Dacă A– începutul vectorului, B este sfârșitul său, atunci vectorul este notat prin simbol; în plus, vectorul este adesea notat cu o singură literă. În figură, vectorul este indicat printr-un segment, iar direcția acestuia printr-o săgeată.

Modul sau lungime Un vector se numește lungimea segmentului direcționat care îl definește. Notat cu || sau ||.

Vom include și așa-numitul vector zero, al cărui început și sfârșit coincid, ca vectori. Este desemnat. Vectorul zero nu are o direcție specifică și modulul său este zero ||=0.

Se numesc vectori coliniare, dacă sunt situate pe aceeași linie sau pe linii paralele. Mai mult, dacă vectorii și sunt în aceeași direcție, vom scrie , opus.

Se numesc vectori situati pe drepte paralele cu acelasi plan coplanare.

Cei doi vectori sunt numiți egal, dacă sunt coliniare, au aceeași direcție și sunt egale ca lungime. În acest caz ei scriu .

Din definiția egalității vectorilor rezultă că un vector poate fi transportat paralel cu el însuși, plasându-și originea în orice punct din spațiu.

De exemplu .

OPERAȚII LINEARE PE VECTORI

Înmulțirea unui vector cu un număr.

Produsul unui vector și numărul λ este un vector nou astfel încât:

Produsul unui vector și unui număr λ se notează cu .

De exemplu, există un vector îndreptat în aceeași direcție cu vectorul și având o lungime pe jumătate mai mare decât vectorul.

Operația introdusă are următoarele proprietăți:

Adăugarea vectorului.

Fie și doi vectori arbitrari. Să luăm un punct arbitrar Oși construiește un vector. După aceea de la punct A să lăsăm vectorul deoparte. Se numește vectorul care leagă începutul primului vector cu sfârșitul celui de-al doilea Cantitate dintre acești vectori și se notează .

Definiția formulată a adunării vectoriale se numește regula paralelogramului, deoarece aceeași sumă de vectori poate fi obținută după cum urmează. Să amânăm de la punct O vectori și . Să construim un paralelogram pe acești vectori OABC. Deoarece vectori, atunci vector, care este o diagonală a unui paralelogram desenat din vârf O, va fi evident o sumă de vectori.

Este ușor să verificați următoarele proprietăți ale adunării vectoriale.

Diferența vectorială.

Vector, coliniar acest vector, egală ca lungime și direcționată opus, se numește opus vector pentru un vector și se notează cu . Vectorul opus poate fi considerat ca rezultat al înmulțirii vectorului cu numărul λ = –1: .

www.site vă permite să găsiți. Site-ul efectuează calculul. În câteva secunde serverul va emite solutie corecta. Ecuația caracteristică pentru matrice va fi o expresie algebrică găsită conform regulii de calcul a determinantului matricei matricei, în timp ce diagonala principală va fi diferența dintre valorile elementelor diagonale și variabilei. La calcularea ecuației caracteristice pentru o matrice online, fiecare element al matricei va fi înmulțit cu celelalte elemente corespunzătoare ale matricei. Îl puteți găsi online doar pentru o matrice pătrată. Operația de găsire a ecuației caracteristice pentru o matrice online se reduce la calcularea sumei algebrice a produsului elementelor matricei ca urmare a găsirii determinantului matricei, numai în scopul determinării ecuației caracteristice pentru online. matrice. Această operație ocupă un loc special în teoria matricelor; vă permite să găsiți valori proprii și vectori folosind rădăcini. Sarcina de a găsi ecuația caracteristică pentru o matrice online este de a înmulți elementele matricei cu însumarea ulterioară a acestor produse prin o anumită regulă. www.site găsește online ecuația caracteristică pentru o matrice de o anumită dimensiune. Calcularea ecuației caracteristice pentru o matrice online pentru o anumită dimensiune înseamnă găsirea unui polinom cu coeficienți numerici sau simbolici, găsit conform regulii de calcul a determinantului unei matrice - ca sumă a produselor elementelor corespunzătoare ale matricei, numai pentru scopul determinării ecuației caracteristice pentru matrice online. Găsirea unui polinom în raport cu o variabilă pentru o matrice pătrată, ca definiție a ecuației caracteristice pentru matrice, este comună în teoria matricei. Valoarea rădăcinilor polinomului ecuației caracteristice pentru o matrice online este utilizată pentru a determina vectorii și valorile proprii pentru matrice. Mai mult, dacă determinantul matricei este egal cu zero, atunci ecuația caracteristică a matricei va exista în continuare, spre deosebire de matricea inversă. Pentru a calcula ecuația caracteristică pentru o matrice sau pentru a găsi ecuații caracteristice pentru mai multe matrice deodată, trebuie să petreceți mult timp și efort, în timp ce serverul nostru va găsi ecuația caracteristică pentru o matrice online în câteva secunde. În acest caz, răspunsul la găsirea ecuației caracteristice pentru o matrice online va fi corect și cu suficientă acuratețe, chiar dacă numerele la găsirea ecuației caracteristice pentru o matrice online vor fi iraționale. Pe site-ul www.site sunt permise intrări simbolice în elemente de matrice, adică ecuația caracteristică pentru o matrice online poate fi reprezentată în formă simbolică generală la calcularea ecuației caracteristice a unei matrice online. Este util să verificați răspunsul obținut la rezolvarea problemei găsirii ecuației caracteristice pentru o matrice online folosind site-ul www.site. Când efectuați operația de calcul a unui polinom - ecuația caracteristică a unei matrice, trebuie să fiți atenți și extrem de concentrați atunci când rezolvați această problemă. La rândul său, site-ul nostru vă va ajuta să vă verificați soluția pe tema ecuației caracteristice a unei matrice online. Dacă nu aveți timp pentru verificări lungi ale problemelor rezolvate, atunci www.site-ul va fi cu siguranță un instrument convenabil de verificare la găsirea și calcularea ecuației caracteristice pentru o matrice online.

Cum se inserează formule matematice pe un site web?

Dacă vreodată trebuie să adăugați una sau două formule matematice pe o pagină web, atunci cel mai simplu mod de a face acest lucru este descris în articol: formulele matematice sunt ușor de inserat pe site sub formă de imagini care sunt generate automat de Wolfram Alpha . Pe lângă simplitate, această metodă universală va ajuta la îmbunătățirea vizibilității site-ului în motoarele de căutare. Funcționează de mult timp (și cred că va funcționa pentru totdeauna), dar este deja depășit din punct de vedere moral.

Dacă utilizați în mod regulat formule matematice pe site-ul dvs., atunci vă recomand să utilizați MathJax - o bibliotecă JavaScript specială care afișează notații matematice în browserele web folosind markup MathML, LaTeX sau ASCIIMathML.

Există două moduri de a începe să utilizați MathJax: (1) folosind un cod simplu, puteți conecta rapid un script MathJax la site-ul dvs., care va fi încărcat automat de pe un server la distanță la momentul potrivit (lista de servere); (2) descărcați scriptul MathJax de pe un server la distanță pe serverul dvs. și conectați-l la toate paginile site-ului dvs. A doua metodă - mai complexă și consumatoare de timp - va grăbi încărcarea paginilor site-ului dvs., iar dacă serverul MathJax părinte devine temporar indisponibil dintr-un motiv oarecare, acest lucru nu vă va afecta în niciun fel propriul site. În ciuda acestor avantaje, am ales prima metodă deoarece este mai simplă, mai rapidă și nu necesită abilități tehnice. Urmează-mi exemplul și în doar 5 minute vei putea folosi toate funcțiile MathJax de pe site-ul tău.

Puteți conecta scriptul de bibliotecă MathJax de la un server la distanță folosind două opțiuni de cod preluate de pe site-ul principal MathJax sau de pe pagina de documentație:

Una dintre aceste opțiuni de cod trebuie să fie copiată și lipită în codul paginii dvs. web, de preferință între etichete și/sau imediat după etichetă. Conform primei opțiuni, MathJax se încarcă mai repede și încetinește pagina mai puțin. Dar a doua opțiune monitorizează și încarcă automat cele mai recente versiuni de MathJax. Dacă introduceți primul cod, acesta va trebui actualizat periodic. Dacă introduceți al doilea cod, paginile se vor încărca mai lent, dar nu va trebui să monitorizați în mod constant actualizările MathJax.

Cel mai simplu mod de a conecta MathJax este în Blogger sau WordPress: în panoul de control al site-ului, adăugați un widget conceput pentru a insera cod JavaScript terță parte, copiați prima sau a doua versiune a codului de descărcare prezentat mai sus în el și plasați widgetul mai aproape la începutul șablonului (apropo, acest lucru nu este deloc necesar, deoarece scriptul MathJax este încărcat asincron). Asta e tot. Acum aflați sintaxa de marcare a MathML, LaTeX și ASCIIMathML și sunteți gata să inserați formule matematice în paginile web ale site-ului dvs.

Orice fractal este construit după o anumită regulă, care este aplicată în mod constant de un număr nelimitat de ori. Fiecare astfel de timp se numește iterație.

Algoritmul iterativ pentru construirea unui burete Menger este destul de simplu: cubul original cu latura 1 este împărțit de planuri paralele cu fețele sale în 27 de cuburi egale. Un cub central și 6 cuburi adiacente acestuia de-a lungul fețelor sunt îndepărtate din el. Rezultatul este un set format din restul de 20 de cuburi mai mici. Făcând același lucru cu fiecare dintre aceste cuburi, obținem un set format din 400 de cuburi mai mici. Continuând acest proces la nesfârșit, obținem un burete Menger.

„Prima parte stabilește prevederile care sunt minim necesare pentru înțelegerea chimiometriei, iar a doua parte conține faptele pe care trebuie să le cunoașteți pentru o înțelegere mai profundă a metodelor de analiză multivariată. Prezentarea este ilustrată cu exemple realizate în caietul de lucru Excel. Matrix.xls, care însoțește acest document.

Legăturile către exemple sunt plasate în text ca obiecte Excel. Aceste exemple sunt de natură abstractă; ele nu sunt în niciun fel legate de problemele chimiei analitice. Exemple din viața reală de utilizare a algebrei matriceale în chimiometrie sunt discutate în alte texte care acoperă o varietate de aplicații chimiometrice.

Majoritatea măsurătorilor efectuate în chimia analitică nu sunt directe, dar indirect. Aceasta înseamnă că în experiment, în locul valorii analitului dorit C (concentrația), se obține o altă valoare. X(semnal), înrudit dar nu egal cu C, i.e. X(C) ≠ C. De regulă, tipul de dependență X(C) este necunoscut, dar din fericire în chimia analitică, majoritatea măsurătorilor sunt proporționale. Aceasta înseamnă că, odată cu creșterea concentrației de C în A de ori, semnalul X va crește cu aceeași cantitate, adică X(A C) = un x(C). În plus, semnalele sunt și aditive, deci semnalul de la o probă în care sunt prezente două substanțe cu concentrații C 1 și C 2 va fi egal cu suma semnalelor de la fiecare componentă, adică. X(C1 + C2) = X(C1)+ X(C 2). Proporționalitatea și aditivitatea împreună dau liniaritatea. Pot fi date multe exemple pentru a ilustra principiul liniarității, dar este suficient să menționăm cele două exemple cele mai izbitoare - cromatografia și spectroscopie. A doua caracteristică inerentă unui experiment de chimie analitică este multicanal. Echipamentele analitice moderne măsoară simultan semnalele pentru mai multe canale. De exemplu, intensitatea transmisiei luminii este măsurată pentru mai multe lungimi de undă simultan, adică gamă. Prin urmare, în experiment ne ocupăm de multe semnale X 1 , X 2 ,...., X n, care caracterizează ansamblul concentraţiilor C 1 , C 2 , ..., C m de substanţe prezente în sistemul studiat.

Orez. 1 Spectre

Deci, un experiment analitic este caracterizat de liniaritate și multidimensionalitate. Prin urmare, este convenabil să se considere datele experimentale ca vectori și matrice și să le manipuleze folosind aparatul algebrei matriceale. Productivitatea acestei abordări este ilustrată de exemplul prezentat în, care prezintă trei spectre luate la 200 de lungimi de undă de la 4000 la 4796 cm -1. Primul (x 1) și al doilea (x 2) spectre au fost obținute pentru probe standard în care sunt cunoscute concentrațiile a două substanțe A și B: în prima probă [A] = 0,5, [B] = 0,1 și în a doua probă [A] = 0,2, [B] = 0,6. Ce se poate spune despre o probă nouă, necunoscută, al cărei spectru este desemnat x 3?

Să considerăm trei spectre experimentale x 1, x 2 și x 3 ca trei vectori de dimensiunea 200. Folosind algebra liniară, putem arăta cu ușurință că x 3 = 0,1 x 1 +0,3 x 2, prin urmare, în cea de-a treia probă, numai substanțele A și B sunt în mod evident prezente în concentrații [A] = 0,5×0,1 + 0,2×0,3 = 0,11 și [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Informații de bază 1.1 Matrici

Matrice numit tabel dreptunghiular de numere, de exemplu

Orez. 2 Matrice

Matricele sunt notate cu majuscule aldine (A), iar elementele lor prin litere mici corespunzătoare cu indici, i.e. A ij. Primul index numește rândurile, iar al doilea - coloanele. În chimiometrie, se obișnuiește să se noteze valoarea maximă a unui index cu aceeași literă ca și indicele în sine, dar cu majuscule. Prin urmare, matricea A poate fi scrisă și ca ( A ij , i = 1,..., eu; j = 1,..., J). Pentru exemplul de matrice eu = 4, J= 3 și A 23 = −7.5.

Pereche de numere euȘi J se numește dimensiunea matricei și se notează ca eu× J. Un exemplu de matrice în chimiometrie este un set de spectre obţinute pentru eu mostre pentru J lungimi de undă.

1.2. Cele mai simple operații cu matrici

Matricele pot fi inmultiti cu numere. În acest caz, fiecare element este înmulțit cu acest număr. De exemplu -

Orez. 3 Înmulțirea unei matrice cu un număr

Două matrice de aceeași dimensiune pot fi element cu element pliazăȘi scădea. De exemplu,

Orez. 4 Adăugarea matricei

Ca rezultat al înmulțirii cu un număr și al adunării, se obține o matrice de aceeași dimensiune.

O matrice zero este o matrice formată din zerouri. Se notează O. Evident, A +O = A, A −A = O și 0A = O.

Matricea poate fi transpune. În timpul acestei operațiuni, matricea este răsturnată, adică rândurile și coloanele sunt schimbate. Transpunerea este indicată de un prim, A" sau indice A t. Astfel, dacă A = ( A ij , i = 1,..., eu; j = 1,...,J), atunci A t = ( A ji , j = 1,...,J; i = 1,..., eu). De exemplu

Orez. 5 Transpunerea matricei

Este evident că (A t) t = A, (A + B) t = A t + B t.

1.3. Înmulțirea matricei

Matricele pot fi multiplica, dar numai dacă au dimensiunile corespunzătoare. De ce este așa va fi clar din definiție. Produsul matricei A, dimensiune eu× K, iar matricea B, dimensiunea K× J, numită matricea C, dimensiune eu× J, ale căror elemente sunt numere

Astfel, pentru produsul AB este necesar ca numărul de coloane din matricea din stânga A să fie egal cu numărul de rânduri din matricea din dreapta B. Un exemplu de produs matrice -

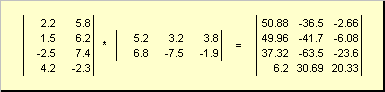
Fig.6 Produsul matricelor

Regula pentru înmulțirea matricei poate fi formulată după cum urmează. Pentru a găsi un element al matricei C la intersecție i-a linia și j a coloana ( c ij) trebuie înmulțit element cu element i-al-lea rând al primei matrice A pe j a doua coloană a celei de-a doua matrice B și adăugați toate rezultatele. Deci, în exemplul prezentat, un element din al treilea rând și din a doua coloană este obținut ca sumă a produselor pe elemente ale celui de-al treilea rând A și a doua coloană B

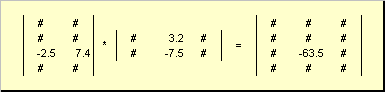
Fig.7 Element al produsului matricelor

Produsul matricelor depinde de ordine, i.e. AB ≠ BA, cel puțin din motive dimensionale. Ei spun că nu este comutativ. Totuși, produsul matricelor este asociativ. Aceasta înseamnă că ABC = (AB)C = A(BC). În plus, este și distributiv, adică A (B +C) = AB +AC. Evident AO = O.

1.4. Matrici pătrate

Dacă numărul coloanelor matricei este egal cu numărul rândurilor sale ( eu = J=N), atunci o astfel de matrice se numește pătrat. În această secțiune vom lua în considerare numai astfel de matrici. Dintre aceste matrici se pot distinge matrice cu proprietăți speciale.

Singur matricea (notată I, iar uneori E) este o matrice în care toate elementele sunt egale cu zero, cu excepția celor diagonale, care sunt egale cu 1, adică.

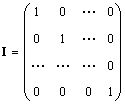
Evident AI = IA = A.

Matricea se numește diagonală, dacă toate elementele sale, cu excepția celor diagonale ( A ii) sunt egale cu zero. De exemplu

Orez. 8 Matrice diagonală

Matricea A se numește superioară triunghiular, dacă toate elementele sale situate sub diagonală sunt egale cu zero, i.e. A ij= 0, la i>j. De exemplu

Orez. 9 Matricea triunghiulară superioară

Matricea triunghiulară inferioară este definită în mod similar.

Matricea A se numește simetric, dacă A t = A . Cu alte cuvinte A ij = A ji. De exemplu

Orez. 10 Matricea simetrică

Matricea A se numește ortogonală, Dacă

A t A = AA t = I .

Matricea se numește normal Dacă

1.5. Urmă și determinant

Următorul matricea pătrată A (notată cu Tr(A) sau Sp(A)) este suma elementelor sale diagonale,

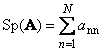
De exemplu,

Orez. 11 Urmă matrice

Este evident că

Sp(α A ) = α Sp(A ) și

Sp(A +B) = Sp(A)+ Sp(B).

Se poate arăta că

Sp(A) = Sp(A t), Sp(I) = N,

și de asemenea că

Sp(AB) = Sp(BA).

O altă caracteristică importantă a unei matrice pătrate este ea determinant(notat det(A )). Definiţia determinant in caz general destul de complicat, așa că vom începe cu cea mai simplă opțiune - o matrice A de dimensiune (2x2). Apoi

Pentru o matrice (3×3) determinantul va fi egal cu

În cazul matricei ( N× N) determinantul se calculează ca suma 1·2·3· ... · N= N! termeni, fiecare dintre acestea fiind egal

Indici k 1 , k 2 ,..., k N sunt definite ca toate permutările ordonate posibile r numerele din multime (1, 2, ..., N). Calcularea determinantului unei matrice este o procedură complexă, care în practică se realizează folosind programe speciale. De exemplu,

Orez. 12 Determinant de matrice

Să notăm doar proprietățile evidente:

det(I ) = 1, det(A ) = det(A t),

det(AB) = det(A)det(B).

1.6. Vectori

Dacă matricea constă dintr-o singură coloană ( J= 1), atunci un astfel de obiect este numit vector. Mai precis, un vector coloană. De exemplu

De asemenea, se pot lua în considerare matrici formate dintr-un rând, de exemplu

Acest obiect este, de asemenea, un vector, dar vector rând. Când analizăm datele, este important să înțelegem cu ce vectori avem de-a face - coloane sau rânduri. Deci, spectrul luat pentru o probă poate fi considerat ca un vector rând. Apoi, setul de intensități spectrale la o anumită lungime de undă pentru toate probele ar trebui tratat ca un vector coloană.

Dimensiunea unui vector este numărul elementelor sale.

Este clar că orice vector coloană poate fi transformat într-un vector rând prin transpunere, adică.

În cazurile în care forma vectorului nu este specificată în mod specific, ci pur și simplu se spune că este un vector, atunci ele înseamnă un vector coloană. De asemenea, vom respecta această regulă. Un vector este notat cu o literă minusculă, dreaptă, aldine. Un vector zero este un vector ale cărui elemente sunt zero. Este desemnat 0.

1.7. Cele mai simple operații cu vectori

Vectorii pot fi adunați și înmulțiți cu numere în același mod ca matricele. De exemplu,

Orez. 13 Operații cu vectori

Se numesc doi vectori x si y coliniar, dacă există un număr α astfel încât

1.8. Produse ale vectorilor

Doi vectori de aceeași dimensiune N poate fi multiplicat. Fie doi vectori x = ( X 1 , X 2 ,...,X N) t și y = ( y 1 , y 2 ,...,y N) t . Ghidați de regula înmulțirii rând cu coloană, putem compune două produse din ele: x t y și xy t. Prima lucrare

numit scalar sau intern. Rezultatul său este un număr. Notația (x ,y )= x t y este de asemenea folosită pentru aceasta. De exemplu,

Orez. 14 Produs interior (scalar).

A doua piesa

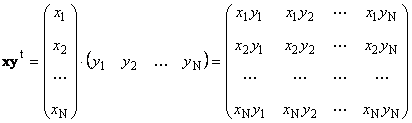
numit extern. Rezultatul său este o matrice de dimensiuni ( N× N). De exemplu,

Orez. 15 Lucrări externe

Vectori, produs scalar care este egal cu zero se numesc ortogonală.

1.9. Norma vectoriala

Produsul scalar al unui vector cu el însuși se numește pătrat scalar. Această valoare

definește un pătrat lungime vector x. Pentru a indica lungimea (numită și norma vector) se folosește notația

De exemplu,

Orez. 16 Norma vectoriala

Un vector de unitate de lungime (||x || = 1) se numește normalizat. Un vector diferit de zero (x ≠ 0) poate fi normalizat prin împărțirea lui la lungimea sa, i.e. x = ||x || (x/ ||x ||) = ||x || e. Aici e = x/ ||x || - vector normalizat.

Vectorii sunt numiți ortonormali dacă toți sunt normalizați și ortogonali pe perechi.

1.10. Unghiul dintre vectori

Produsul scalar determină și colţφ între doi vectori x și y

Dacă vectorii sunt ortogonali, atunci cosφ = 0 și φ = π/2, iar dacă sunt coliniari, atunci cosφ = 1 și φ = 0.

1.11. Reprezentarea vectorială a unei matrice

Fiecare matrice A de dimensiune eu× J poate fi reprezentat ca un set de vectori

Aici fiecare vector a j este j a-a coloană și vectorul rând b i este i al treilea rând al matricei A

1.12. Vectori dependenți liniar

Vectori de aceeași dimensiune ( N) poate fi adăugat și înmulțit cu un număr, la fel ca matricele. Rezultatul va fi un vector de aceeași dimensiune. Să fie mai mulți vectori de aceeași dimensiune x 1, x 2,...,x K și același număr de numere α α 1, α 2,...,α K. Vector

y = α 1 x 1 + α 2 x 2 +...+ α K X K

numit combinație liniară vectorii x k .

Dacă există astfel de numere diferite de zero α k ≠ 0, k = 1,..., K că y = 0, atunci un astfel de set de vectori x k numit dependent liniar. În caz contrar, se spune că vectorii sunt independenți liniar. De exemplu, vectorii x 1 = (2, 2) t și x 2 = (−1, −1) t sunt dependenți liniar, deoarece x 1 +2x 2 = 0

1.13. Rangul matricei

Luați în considerare un set de K vectori x 1 , x 2 ,...,x K dimensiuni N. Rangul acestui sistem de vectori este numărul maxim de vectori liniar independenți. De exemplu, în set

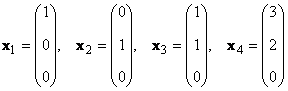
există doar doi vectori liniar independenți, de exemplu x 1 și x 2, deci rangul său este 2.

Evident, dacă există mai mulți vectori într-o mulțime decât dimensiunea lor ( K>N), atunci ele sunt în mod necesar dependente liniar.

Rangul matricei(notat cu rang(A)) este rangul sistemului de vectori din care este format. Deși orice matrice poate fi reprezentată în două moduri (vectori coloană sau rând), acest lucru nu afectează valoarea rangului, deoarece

1.14. matrice inversă

O matrice pătrată A se numește nesingulară dacă are un unic verso matricea A -1 determinată de condiţii

AA −1 = A −1 A = I .

Matricea inversă nu există pentru toate matricele. O condiție necesară și suficientă pentru non-degenerare este

det(A) ≠ 0 sau rang(A) = N.

Inversarea matricei este o procedură complexă pentru care există programe speciale. De exemplu,

Orez. 17 Inversarea matricei

Să prezentăm formulele pentru cel mai simplu caz - o matrice 2×2

Dacă matricele A și B sunt nesingulare, atunci

(AB ) −1 = B −1 A −1 .

1.15. Pseudo matrice inversă

Dacă matricea A este singulară și matricea inversă nu există, atunci în unele cazuri puteți utiliza pseudoinvers matrice, care este definită ca o matrice A+ astfel încât

AA + A = A.

Matricea pseudoinversă nu este singura, iar forma sa depinde de metoda de construcție. De exemplu, pentru o matrice dreptunghiulară puteți folosi metoda Moore-Penrose.

Dacă numărul de coloane număr mai mic linii, atunci

A + =(A t A ) −1 A t

De exemplu,

Orez. 17a Pseudo-inversie a unei matrice

Dacă numărul de coloane mai mult număr linii, atunci

A + =A t (AA t) −1

1.16. Înmulțirea unui vector cu o matrice

Vectorul x poate fi înmulțit cu o matrice A de dimensiune adecvată. În acest caz, vectorul coloană este înmulțit pe Ax din dreapta, iar vectorul rând este înmulțit pe stânga x t A. Dacă dimensiunea vectorială J, și dimensiunea matricei eu× J atunci rezultatul va fi un vector de dimensiune eu. De exemplu,

Orez. 18 Înmulțirea unui vector cu o matrice

Dacă matricea A este pătrată ( eu× eu), atunci vectorul y = Ax are aceeași dimensiune ca x. Este evident că

A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Prin urmare, matricele pot fi considerate transformări liniare ale vectorilor. În special, Ix = x, Ox = 0.

2. Informații suplimentare 2.1. Sisteme de ecuații liniare

Fie A o matrice de dimensiune eu× J, iar b este vectorul dimensiune J. Luați în considerare ecuația

Ax = b

raportat la vectorul x, dimensiunea eu. În esență, este un sistem de eu ecuații liniare cu J necunoscut X 1 ,...,X J. O soluție există dacă și numai dacă

rang(A) = rang(B) = R,

unde B este matricea dimensiunilor augmentate eu×( J+1), constând dintr-o matrice A completată de o coloană b, B = (A b). În caz contrar, ecuațiile sunt inconsistente.

Dacă R = eu = J, atunci soluția este unică

x = A −1 b .

Dacă R < eu, atunci sunt multe diverse solutii, care poate fi exprimat printr-o combinație liniară J−R vectori. Sistem de ecuații omogene Ax = 0 cu matrice pătrată A ( N× N) are o soluție netrivială (x ≠ 0) dacă și numai dacă det(A) = 0. Dacă R= rang (A) 0.

Definit în mod similar negativ(x t Ax< 0), nenegativ(x t Ax ≥ 0) și negativ(x t Ax ≤ 0) anumite matrici.

2.4. Descompunerea Cholesky

Dacă o matrice simetrică A este definită pozitiv, atunci există o matrice triunghiulară unică U cu elemente pozitive pentru care

A = U t U .

De exemplu,

Orez. 19 Descompunerea Cholesky

2.5. Descompunerea polară

Fie A o matrice pătrată nesingulară de dimensiune N× N. Apoi există un unic polar performanţă

A = SR,

unde S este o matrice simetrică nenegativă și R este o matrice ortogonală. Matricele S și R pot fi definite explicit:

S 2 = AA t sau S = (AA t) ½ și R = S −1 A = (AA t) −½ A .

De exemplu,

Orez. 20 Descompunerea polară

Dacă matricea A este singulară, atunci descompunerea nu este unică - și anume: S este încă unul, dar pot fi multe R. Descompunerea polară reprezintă matricea A ca o combinație de compresie/extensie S și rotație R .

2.6. Vectori proprii și valori proprii

Fie A o matrice pătrată. Se numește vectorul v vector propriu matricea A dacă

Av = λv,

unde se numește numărul λ valoare proprie matricele A. Astfel, transformarea pe care o realizează matricea A asupra vectorului v se reduce la o simplă întindere sau compresie cu un coeficient λ. Vectorul propriu este determinat până la înmulțire cu o constantă α ≠ 0, adică. dacă v este un vector propriu, atunci αv este, de asemenea, un vector propriu.

2.7. Valori proprii

Matricea A are dimensiunea ( N× N) nu poate fi mai mult de N valori proprii. Ei satisfac ecuație caracteristică

det(A − λI ) = 0,

fiind ecuație algebrică N-a comanda. În special, pentru o matrice 2×2 ecuația caracteristică are forma

De exemplu,

Orez. 21 Valori proprii

Mulțimea valorilor proprii λ 1 ,..., λ N se numeste matricea A spectru A.

Spectrul are proprietăți diferite. În special

det(A ) = λ 1 ×...×λ N, Sp(A) = λ 1 +...+λ N.

Valorile proprii ale unei matrice arbitrare pot fi numere complexe, dar dacă matricea este simetrică (A t = A), atunci valorile sale proprii sunt reale.

2.8. Vectori proprii

Matricea A are dimensiunea ( N× N) nu poate fi mai mult de N vectori proprii, fiecare dintre care corespunde propriei valori proprii. Pentru a determina vectorul propriu v n trebuie să rezolvăm un sistem de ecuații omogene

(A - λ n eu) v n = 0 .

Are o soluție netrivială, deoarece det(A − λ n I) = 0.

De exemplu,

Orez. 22 de vectori proprii

Vectorii proprii ai unei matrice simetrice sunt ortogonali.