Această lecție îi va ajuta pe cei care doresc să înțeleagă subiectul „Semnul perpendicularității a două planuri”. La începutul acesteia, vom repeta definiția unghiurilor diedrice și liniare. Apoi vom lua în considerare care planuri sunt numite perpendiculare și vom demonstra semnul perpendicularității a două plane.

Tema: Perpendicularitatea dreptelor și a planurilor

Lecția: Semnul perpendicularității a două plane

Definiţie. Un unghi diedru este o figură formată din două semiplane care nu aparțin aceluiași plan și linia lor dreaptă comună a (a este o muchie).

Orez. 1

Să considerăm două semiplane α și β (Fig. 1). Granița lor comună este l. Această figură se numește unghi diedru. Două plane care se intersectează formează patru unghiuri diedrice cu o muchie comună.

Un unghi diedru se măsoară prin unghiul său liniar. Alegem un punct arbitrar pe muchia comună l a unghiului diedric. În semiplanele α și β, din acest punct tragem perpendiculare a și b pe dreapta l și obținem unghiul liniar al unghiului diedru.

Liniile drepte a și b formează patru unghiuri egale cu φ, 180° - φ, φ, 180° - φ. Amintiți-vă că unghiul dintre liniile drepte este cel mai mic dintre aceste unghiuri.

Definiţie. Unghiul dintre plane este cel mai mic dintre unghiurile diedrice formate de aceste plane. φ este unghiul dintre planele α și β, dacă

Definiţie. Două plane care se intersectează sunt numite perpendiculare (perpendiculare reciproce) dacă unghiul dintre ele este de 90°.

Orez. 2

Un punct arbitrar M este selectat pe muchia l (Fig. 2). Să desenăm două drepte perpendiculare MA = a și MB = b pe muchia l în planul α și, respectiv, în planul β. Avem unghiul AMB. Unghiul AMB este unghiul liniar al unui unghi diedru. Dacă unghiul AMB este de 90°, atunci planurile α și β se numesc perpendiculare.

Linia b este perpendiculară pe dreapta l prin construcție. Linia b este perpendiculară pe dreapta a, deoarece unghiul dintre planele α și β este de 90°. Constatăm că dreapta b este perpendiculară pe două drepte care se intersectează a și l din planul α. Aceasta înseamnă că dreapta b este perpendiculară pe planul α.

În mod similar, putem demonstra că dreapta a este perpendiculară pe planul β. Linia a este perpendiculară pe dreapta l prin construcție. Linia a este perpendiculară pe dreapta b, deoarece unghiul dintre planele α și β este de 90°. Constatăm că linia a este perpendiculară pe două drepte care se intersectează b și l din planul β. Aceasta înseamnă că dreapta a este perpendiculară pe planul β.

Dacă unul dintre cele două plane trece printr-o linie perpendiculară pe celălalt plan, atunci astfel de planuri sunt perpendiculare.

Dovedi:

Orez. 3

Dovada:

Fie că planele α și β se intersectează de-a lungul dreptei AC (Fig. 3). Pentru a demonstra că planurile sunt reciproc perpendiculare, trebuie să construiți un unghi liniar între ele și să arătați că acest unghi este de 90°.

Linia dreaptă AB este perpendiculară pe planul β și, prin urmare, pe dreapta AC aflată în planul β.

Să desenăm o dreaptă AD perpendiculară pe o dreaptă AC în planul β. Atunci BAD este unghiul liniar al unghiului diedru.

Linia dreaptă AB este perpendiculară pe planul β și, prin urmare, pe dreapta AD aflată în planul β. Aceasta înseamnă că unghiul liniar BAD este de 90°. Aceasta înseamnă că planurile α și β sunt perpendiculare, ceea ce trebuia demonstrat.

Planul perpendicular pe dreapta de-a lungul căreia două plane date se intersectează este perpendicular pe fiecare dintre aceste plane (Fig. 4).

Dovedi:

Orez. 4

Dovada:

Linia dreaptă l este perpendiculară pe planul γ, iar planul α trece prin dreapta l. Aceasta înseamnă că, pe baza perpendicularității planelor, planurile α și γ sunt perpendiculare.

Linia dreaptă l este perpendiculară pe planul γ, iar planul β trece prin dreapta l. Aceasta înseamnă că, în funcție de perpendicularitatea planurilor, planurile β și γ sunt perpendiculare.

Perpendicularitatea planurilor Definiţie. Două plane se numesc perpendiculare dacă unghiul liniar la marginea unghiului diedric dintre aceste plane este o linie dreaptă.
Semn perpendicularitatea planurilor. Dacă un plan trece printr-o dreaptă perpendiculară pe un alt plan, atunci aceste planuri sunt perpendiculare.
Dovada. Lasă oȘi? - două plane care se intersectează, Cu- linia de intersectie a acestora si O- Drept perpendicular pe plan? și întins într-un aviono. A - punctul de intersecție al drepteloroŞi Cu.Într-un avion? din punctȘi ne vom restabili perpendiculară și să fie o linie dreaptă. b O Drept perpendicular perpendiculară și să fie o linie dreaptă avioane? , ceea ce înseamnă că este perpendiculară pe orice dreaptă din acest plan, adică linii drepte CuŞi . perpendicular O Unghiul dintre liniile drepte Şi b - o planuri liniare Și?și este egal cu 90°, deci Cum O Dreptperpendiculară și să fie o linie dreaptăperpendicular pe o linie dreaptăo(dovedit).După definiţia unui plan Și?

perpendicular.. Dacă dintr-un punct aparținând unuia dintre cele două plane perpendiculare, desenați perpendiculară pe un alt plan, atunci această perpendiculară se află în întregime în primul plan.
Dovada. Lasă oȘi? - planuri perpendiculare şi Cu - linia dreaptă a intersecției lor, punctul A culcat plat oși nu aparținând direct Cu. Perpendicular pe plan? trasat din punctul A nu se află în plan o, atunci punctul C este baza această perpendiculară se află în avioane? Cu. si nu apartine liniei Din punctul A coborâm perpendiculara AB Cu. directLinia AB este perpendicularăplan (folosesc Teorema 2).Prin dreapta AB și punctul C Să desenăm un avion? ? (o linie dreaptă și un punct definesc un plan și doar unul). Vedem asta în avion o.

de la un punct A la dreapta BC se trasează două perpendiculare, ceea ce nu se poate întâmpla, ceea ce înseamnă dreaptă AC. coincide cu dreapta AB, iar dreapta AB, la rândul ei, se află complet în planTeorema 2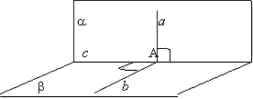
Dovada. Lasă o Dacă în unul din cele două plane perpendiculare tragem o perpendiculară pe dreapta lor Cu - intersecție, atunci această perpendiculară va fi perpendiculară pe al doilea plan. Și? - două plane perpendiculare, linia de intersectie a acestora si A - Cuși întins într-un avionoDrept O Unghiul dintre liniile drepte Cu. perpendicular pe o linie dreaptă. A - punctul de intersecție a dreptelor În avion? O avioane? , ceea ce înseamnă că este perpendiculară pe orice dreaptă din acest plan, adică linii drepteperpendiculară și să fie o linie dreaptă din punctul A restabilim perpendiculara și o lăsăm drept dreaptă b. Unghiul dintre liniile drepte o- liniară unghi la marginea unghiului diedru dintreo avioane Și? Oși este egal cu 90°, deoarece planulperpendiculară și să fie o linie dreaptăȘi? Cu perpendicular. Drept perpendicular pe o linie dreaptă O(după dovedit) și direct

dupa conditie.

Deci e drept

perpendicular pe plan?

(

Prelegere pe tema „Testul de perpendicularitate a două planuri”

Ideea unui avion în spațiu ne permite să obținem, de exemplu, suprafața unei mese sau a unui perete. Cu toate acestea, o masă sau un perete are dimensiuni finite, iar planul se extinde dincolo de limitele sale până la infinit. 0 Luați în considerare două plane care se intersectează. Când se intersectează, formează patru unghiuri diedrice cu o margine comună. 0 -).

α Să ne amintim ce este un unghi diedru.β, 0°< 90 °

În realitate, întâlnim obiecte care au forma unui unghi diedru: de exemplu, o ușă ușor deschisă sau un dosar întredeschis. 0 .

Când două plane alfa și beta se intersectează, obținem patru unghiuri diedre. Fie unul dintre unghiurile diedrice egal cu (phi), apoi al doilea este egal cu (180 0 .

–), al treilea, al patrulea (180α Să ne amintim ce este un unghi diedru.β,

Şi

Luați în considerare cazul în care unul dintre unghiurile diedrice este de 90

Două plane se numesc perpendiculare dacă unghiul diedric dintre ele este de 90°.

Unghiul dintre planurile sigma și epsilon este de 90 de grade, ceea ce înseamnă că planurile sunt perpendiculare

Deoarece =90°

Să dăm exemple de planuri perpendiculare.

Perete și tavan.

Peretele lateral și blatul mesei.

Perete și tavan

Să formulăm un semn de perpendicularitate a două plane:

TEOREMA:Dacă unul dintre cele două plane trece printr-o linie perpendiculară pe celălalt plan, atunci aceste planuri sunt perpendiculare.

Să demonstrăm acest semn.

Prin condiție se știe că linia dreaptăAM se află în planul α, linia dreaptă AM este perpendiculară pe planul β,

Demonstrați: planurile α și β sunt perpendiculare.

Dovada:

1) Planurile α șiβ se intersectează de-a lungul dreptei AR și AM AR, deoarece AM β prin condiție, adică AM este perpendiculară pe orice dreaptă situată în planul β.

2) Să desenăm o dreaptă în planul βOT perpendicularOR.

Obținem unghiul TOM este unghiul liniar al unghiului diedric. Dar unghiul TOM = 90°, deoarece MA este β. Deci α β.

Q.E.D.

TEOREMA:Dacă un plan trece printr-o dreaptă perpendiculară pe alt plan, atunci aceste planuri sunt perpendiculare.

Dat:α, β, AM α, AMβ, AM∩=A

Demonstrați: αβ.

Dovada:

1) α∩β = AR, în timp ce AM ​​AR, deoarece AM β prin condiție, adică AM este perpendiculară pe orice dreaptă situată în planul β.

2) ATβ,OTOR.

TAM este unghiul liniar al unghiului diedru. TAM = 90°, deoarece MA β. Deci α β.

Q.E.D

Din semnul perpendicularității a două plane avem un corolar important:

IMPACT:Un plan perpendicular pe o dreaptă de-a lungul căreia două plane se intersectează este perpendicular pe fiecare dintre aceste planuri.

Să demonstrăm acest corolar: dacă planul gamma este perpendicular pe dreapta c, atunci, pe baza paralelismului celor două plane, gamma este perpendicular pe alfa. La fel, gamma este perpendicular pe beta

Adică: dacă α∩β=с și γс, atunci γα și γβ.

deoareceγс și сα din semnul perpendicularității γα.

Similar cu γβ

Să reformulăm acest corolar pentru un unghi diedru:

Planul care trece prin unghiul liniar al unui unghi diedru este perpendicular pe muchia și fețele acestui unghi diedru. Cu alte cuvinte, dacă am construit un unghi liniar al unui unghi diedru, atunci planul care trece prin el este perpendicular pe muchia și fețele acestui unghi diedru.

Sarcină.

Având în vedere: ΔАВС, С = 90°, АС se află în planul α, unghiul dintre planele α șiABC= 60°, AC = 5 cm, AB = 13 cm.

Aflați: distanța de la punctul B la planul α.

Soluţie:

1) Să construim VC α. Atunci KS este proiecția soarelui pe acest plan.

2) BC AC (prin condiție), ceea ce înseamnă, conform teoremei celor trei perpendiculare (TPP), KS AC. Prin urmare, VSK este unghiul liniar al unghiului diedric dintre planul α și planul triunghiului ABC. Adică VSK = 60°.

3) Din ΔBCA conform teoremei lui Pitagora:

De la ΔVKS:

Din stereometrie se știe condiția perpendicularității a două plane: dacă un plan trece printr-o perpendiculară pe un plan dat (sau este paralel cu această perpendiculară), atunci este perpendicular pe un plan dat.

Printr-un punct dat A este posibil să se deseneze un număr infinit de plane perpendiculare pe un plan dat P (Fig. 3.19). Aceste planuri formează un mănunchi de plane în spațiu, a cărui axă este perpendiculara AB, coborâtă din punctul A în planul P.

Diagrama (Fig. 3.20) arată construcția unuia dintre planurile acestei grinzi. În primul rând, prin proiecțiile punctului A se trasează proiecții ale perpendicularei AK pe acest plan. Construcția lui A 1 K 1 și A 2 K 2 nu provoacă dificultăți, deoarece planul P este definit de liniile principale. Apoi, prin proiecțiile aceluiași punct A se trasează proiecțiile unei drepte arbitrare AD. Aceste două drepte care se intersectează AK și AD determină planul dorit P.

Exemple de probleme de poziție și metrice pe plan

Exemplul 1 . În planul definit de triunghiul ABC, construiți punctul D (Fig. 3.21).

Soluţie.

1. Este necesar să se traseze o linie dreaptă în acest plan. Pentru a face acest lucru, definim două puncte care se află în mod evident în acest plan. Unul dintre aceste puncte poate fi vârful A(A 1 ;A 2) al triunghiului. Vom seta al doilea punct E(E 1;E 2) pe latura BC. Desenăm linii drepte prin proiecțiile cu același nume A 1 și E 1, A 2 și E 2. Aceste linii sunt proiecții ale liniei. Întins într-un plan dat.

2. Pe dreapta construită AE, setăm punctul D. Pentru aceasta, construim D 1 ОА 1 Е 1 și D 2 ОА 2 Е 2. Punctul D se află într-un plan dat, deoarece aparține dreptei AE care se află în acest plan

Exemplul 2 . Construiți linia cu cea mai mare pantă a planului definit de drepte paralele a(a 1 ; a 2) și b(b 1 ; b 2) și determinați unghiul a dintre acest plan și planul orizontal de proiecție (Fig. 3.22)

Soluţie

1. Să desenăm o linie orizontală h a acestui plan (vezi Capitolul 3, Fig. 3.3, c). Proiecțiile acestei linii orizontale vor fi drepte h 1 și h 2.
2. Să desenăm o linie dreaptă perpendiculară pe proiecția orizontală a orizontalei și să marchem punctele C 1 - intersecția acesteia cu h 1 D 1 - ca 1. Linia dreaptă C 1 D 1 este o proiecție orizontală a dreptei celei mai mari pante.
3. Să construim proiecțiile frontale C 2 și D 2. Pentru a face acest lucru, desenăm linii de comunicație verticale din C 1 și D 1 până când se intersectează cu h 2 și, respectiv, cu a 2.
4. Linia dreaptă care leagă punctele C 2 și D 2 este proiecția frontală a dreptei cu cea mai mare pantă.
5. Unghiul a este determinat dintr-un triunghi dreptunghic D 1 C 1 E 0 construit pe C 1 D 1 ca pe o latură. Manșa a doua D 0 D 1 = E 2 D 2. Unghiul necesar a=ÐD 0 C 1 D 1

Exemplul 3 . Un plan este definit de drepte care se intersectează AB și CD. Determinați dacă linia dreaptă KL se află în acest plan.

Soluţie.

1. Să notăm punctele de intersecție ale proiecțiilor frontale ale dreptelor AB și KL cu 1 2 și ale dreptelor CD și KL cu 2 2 .

2. Construim proiecțiile lor orizontale - punctele 1 1 și 2 2 pe proiecția orizontală (K 1 L 1) a dreptei KL. Din construcție este clar că punctele 1(1 1 1 2) și 2(2 1 2 2) ale dreptei KL nu se află pe planul dat. În consecință, linia KL nu se află în plan. Soluția la această problemă poate începe și cu intersecția proiecțiilor orizontale.

Exemplul 4 . În planul definit de două drepte paralele AB și CD, trasați frontalul la o distanță de 15 mm de planul frontal al proiecțiilor (Fig. 3.24)

Soluţie. La o distanță de 15 mm de axa de proiecție, desenăm o proiecție orizontală (1 1 -2 2) a frontalei paralele cu aceasta, care intersectează liniile drepte A 1 B 1 și C 1 D 1 în punctele 1 1 și 2 2. .

Apoi găsim punctele 1 1 și 2 2 pe liniile drepte A 2 B 2 și C 2 D 2 și trasăm o proiecție frontală (1 2 2 2) a frontalului prin ele.

Exemplul 5 . Aflați dreapta de intersecție a planurilor P și Q.

Soluţie. Planele P și Q se intersectează de-a lungul unei drepte generale care trece prin punctul de urmărire (M 1;M 2) al intersecției urmelor orizontale ale planelor. Punctul de urmărire (N 1 ;N 2) al intersecției urmelor frontale ale planurilor nu este disponibil, deoarece Conform instrucțiunilor, aceste urme de planuri nu se intersectează în cadrul desenului.

În locul punctului (N 1 ;N 2), este necesar să se găsească un alt punct arbitrar al dreptei de intersecție, comun planurilor date. Pentru a face acest lucru, introducem un plan auxiliar R, de exemplu paralel cu П care, după cum se știe, intersectează fiecare dintre aceste planuri orizontal. La intersectia lor obtinem un punct auxiliar (K 1;K 2), comun acestor plane. După ce am găsit acest al doilea punct (K 1;K 2) al dreptei, desenăm proiecția acestuia: orizontală - prin punctele M 1 și K 1 și frontală prin punctele M 2 și K 2.

Exemplul 6 . Aflați punctul de intersecție al dreptei AB cu planul P (Fig. 3.26)

Soluţie. Să notăm punctul dorit cu punctul K. Deoarece punctul K (K 1 ;K 2) se află pe planul de proiectare a profilului. Apoi proiecția sa de profil (K 3) ar trebui să se afle pe urma profilului (P 3) a planului. În același timp, deoarece același punct se află și pe linia dreaptă AB, proiecția sa de profil (K 3) trebuie să se afle undeva pe proiecția de profil (A 3 B 3) a dreptei. Prin urmare, punctul necesar trebuie să se afle la intersecția lor. După ce am găsit urma de profil a planului și proiecția de profil a dreptei, obținem la intersecția acestora proiecția de profil (K 3) a punctului dorit. Cunoscând proiecția de profil (K 3) a punctului dorit, găsim celelalte două proiecții ale acestuia pe aceleași proiecții ale dreptei.

Exemplu 7 . Având în vedere planul P și punctul A. Determinați distanța acelui punct față de plan (Fig. 3.27)

Soluţie. Coborâm o perpendiculară din punctul A (A 1 ;A 2) în planul P și găsim baza ei pe acest plan, pentru care căutăm punctul K (K 1 ;K 2) de intersecție a perpendicularei cu planul. Având proiecțiile (A 1 K 1;A 2 K 2) ale segmentului perpendicular, determinăm valoarea reală a acestuia folosind metoda triunghiului dreptunghic.

Exemplul 8 . Având în vedere un triunghi ABC și un punct K. Să se determine distanța dintre ele. (Fig. 3.28)

Soluţie. Coborâm o perpendiculară dintr-un punct dat E (E 1 ;E 2) pe planul triunghiului: K 1 E 1 perpendicular pe proiecția orizontală a orizontalei (K 1 E 1 ^C 1 F 1), K 2 E 2 perpendicular pe proiecţia frontală a frontalului (K 2 E 2 ^A 2 D 2). Găsim punctul de intersecție al perpendicularei cu planul triunghiului (K 1;K 2), se determină dimensiunea naturală a segmentului perpendicular (K 1 E 1;K 2 E 2) folosind metoda triunghiului dreptunghic.

Capitolul 4

Metode de conversie a unui desen complex (diagrama Monge)