Acum, cu sufletul calm, să trecem la considerare limite minunate.
se pare ca .
În locul variabilei x poate exista diverse funcții, principalul lucru este că au tendința de a fi 0.
Este necesar să se calculeze limita
După cum puteți vedea, această limită este foarte asemănătoare cu prima remarcabilă, dar acest lucru nu este în întregime adevărat. În general, dacă observați păcat în limită, atunci ar trebui să vă gândiți imediat dacă este posibil să folosiți prima limită remarcabilă.
Conform regulii noastre nr. 1, înlocuim zero în loc de x:
Primim incertitudine.
Acum să încercăm să organizăm singuri prima limită minunată. Pentru a face acest lucru, să facem o combinație simplă:
Deci, organizăm numărătorul și numitorul pentru a evidenția 7x. Acum a apărut deja limita remarcabilă familiară. Este recomandabil să o evidențiați atunci când decideți:
Să înlocuim soluția primei exemplu minunat si obtinem:
Simplificarea fracției:
Raspuns: 7/3.
După cum puteți vedea, totul este foarte simplu.
Se pare ca , unde e = 2,718281828... este un număr irațional.
Pot fi prezente diferite funcții în locul variabilei x, principalul lucru este că acestea tind să .
Este necesar să se calculeze limita
Aici vedem prezența unui grad sub semnul unei limite, ceea ce înseamnă că este posibil să se utilizeze o a doua limită remarcabilă.
Ca întotdeauna, vom folosi regula nr. 1 - înlocuiți x în loc de:
Se poate observa că la x baza gradului este , iar exponentul este 4x > , adică. obținem o incertitudine de forma:
Să folosim a doua limită minunată pentru a ne dezvălui incertitudinea, dar mai întâi trebuie să o organizăm. După cum puteți vedea, trebuie să obținem prezența în indicator, pentru care ridicăm baza la puterea de 3x și, în același timp, la puterea de 1/3x, astfel încât expresia să nu se schimbe:
Nu uitați să subliniați limita noastră minunată:
Asta sunt cu adevărat limite minunate!
Dacă mai aveți întrebări despre prima și a doua limite minunate, apoi nu ezitați să-i întrebați în comentarii.
Vom răspunde tuturor cât mai mult posibil.
De asemenea, puteți lucra cu un profesor pe această temă.
Suntem încântați să vă oferim serviciile de selectare a unui tutor calificat în orașul dumneavoastră. Partenerii noștri vor selecta rapid un profesor bun pentru tine, în condiții favorabile.
Nu sunt suficiente informații? - Puteți !
Puteți scrie calcule matematice în blocnotes. Este mult mai plăcut să scrieți individual în caiete cu logo (http://www.blocnot.ru).
Există mai multe limite remarcabile, dar cele mai cunoscute sunt prima și a doua limite remarcabile. Lucrul remarcabil la aceste limite este că sunt utilizate pe scară largă și cu ajutorul lor se pot găsi și alte limite întâlnite în numeroase probleme. Aceasta este ceea ce vom face în partea practică a acestei lecții. Pentru a rezolva probleme reducându-le la prima sau a doua limită remarcabilă, nu este nevoie să dezvăluim incertitudinile conținute în ele, deoarece valorile acestor limite au fost deduse de multă vreme de marii matematicieni.
Prima limită minunată se numește limita raportului dintre sinusul unui arc infinitezimal și același arc, exprimat în radiani:
Să trecem la rezolvarea problemelor la prima limită remarcabilă. Notă: dacă există o funcție trigonometrică sub semnul limită, aceasta este aproape semn sigur că această expresie poate fi dusă la prima ei limită remarcabilă.
Exemplul 1. Găsiți limita.
Soluţie. Înlocuire în schimb X zero duce la incertitudine:
![]() .
.
Numitorul este sinus, prin urmare, expresia poate fi adusă la prima limită remarcabilă. Să începem transformarea:
![]() .
.
Numitorul este sinusul a trei X, dar numărătorul are doar un X, ceea ce înseamnă că trebuie să obțineți trei X la numărător. Pentru ce? A introduce 3 X = Ași obțineți expresia .
Și ajungem la o variație a primei limite remarcabile:
pentru că nu contează ce literă (variabilă) din această formulă este în locul lui X.
Înmulțim X cu trei și împărțim imediat:
 .
.
În conformitate cu prima limită remarcabilă observată, înlocuim expresia fracțională:
Acum putem rezolva în sfârșit această limită:
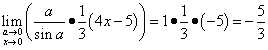 .
.
Exemplul 2. Găsiți limita.
Soluţie. Substituția directă duce din nou la incertitudinea „zero împărțit la zero”:
![]() .
.
Pentru a obține prima limită remarcabilă, este necesar ca x sub semnul sinus la numărător și doar x la numitor să aibă același coeficient. Fie acest coeficient egal cu 2. Pentru a face acest lucru, imaginați-vă coeficientul curent pentru x ca mai jos, efectuând operații cu fracții, obținem:
 .
.
Exemplul 3. Găsiți limita.
Soluţie. Când înlocuim, obținem din nou incertitudinea „zero împărțit la zero”:
 .
.
Probabil că deja înțelegeți că din expresia originală puteți obține prima limită minunată înmulțită cu prima limită minunată. Pentru a face acest lucru, descompunem pătratele lui x la numărător și sinusul la numitor în factori identici, iar pentru a obține aceiași coeficienți pentru x și sinus, împărțim x din numărător cu 3 și imediat înmulțim cu 3. Obținem:
 .
.
Exemplul 4. Găsiți limita.
Soluţie. Din nou, obținem incertitudinea „zero împărțit la zero”:
![]() .
.
Putem obține raportul dintre primele două limite remarcabile. Împărțim atât numărătorul cât și numitorul cu x. Apoi, pentru ca coeficienții pentru sinusuri și axe să coincidă, înmulțim x superior cu 2 și împărțim imediat cu 2 și înmulțim x inferior cu 3 și împărțim imediat cu 3. Obținem:

Exemplul 5. Găsiți limita.
Soluţie. Și din nou incertitudinea „zero împărțit la zero”:
Ne amintim din trigonometrie că tangenta este raportul dintre sinus și cosinus, iar cosinusul lui zero este egal cu unu. Efectuăm transformările și obținem:
 .
.
Exemplul 6. Găsiți limita.
Soluţie. Funcția trigonometrică sub semnul unei limite sugerează din nou utilizarea primei limite remarcabile. O reprezentăm ca raportul dintre sinus și cosinus.
Prima limită remarcabilă este adesea folosită pentru a calcula limitele care conțin sinus, arcsinus, tangentă, arctangentă și incertitudinile rezultate ale zero împărțit la zero.
Formulă
Formula pentru prima limită remarcabilă este: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
Observăm că pentru $ \alpha\to 0 $ obținem $ \sin\alpha \to 0 $, astfel avem zerouri în numărător și numitor. Astfel, formula primei limite remarcabile este necesară pentru a releva incertitudinile $ \frac(0)(0) $.
Pentru a aplica formula, trebuie îndeplinite două condiții:
- Expresiile conținute în sinus și numitorul fracției sunt aceleași
- Expresiile din sinusul și numitorul unei fracții tind spre zero
Atenţie! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Deși expresiile de sub sinus și la numitor sunt aceleași, totuși $ 2x ^2+1 = 1 $, pentru $ x\la 0 $. A doua condiție nu este îndeplinită, așa că NU POȚI aplica formula!
Consecințe
Destul de rar în sarcini puteți vedea o primă limită minunată pură, în care puteți nota imediat răspunsul. În practică, totul pare puțin mai complicat, dar pentru astfel de cazuri va fi util să cunoaștem consecințele primei limite remarcabile. Datorită acestora, puteți calcula rapid limitele necesare.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Exemple de soluții
Să luăm în considerare prima limită remarcabilă, exemple ale soluției sale pentru calcularea limitelor care conțin funcții trigonometrice iar incertitudinea $ \bigg[\frac(0)(0)\bigg] $
| Exemplul 1 |
| Calculați $ \lim_(x\to 0) \frac(\sin2x)(4x) $ |
| Soluţie |
|
Să ne uităm la limită și să observăm că conține un sinus. Apoi, înlocuim $ x = 0 $ în numărător și numitor și obținem incertitudinea zero împărțit la zero: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0) ) $$ Deja două semne că trebuie să aplicăm o limită minunată, dar există o mică nuanță: nu putem aplica imediat formula, deoarece expresia de sub semnul sinus diferă de expresia din numitor. Și avem nevoie de ei să fie egali. Prin urmare, folosind transformări elementare ale numărătorului, îl vom transforma în $2x$. Pentru a face acest lucru, le vom scoate pe cele două din numitorul fracției ca factor separat. Arată astfel: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Vă rugăm rețineți că la sfârșit $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ a fost obținut după formula. Dacă nu vă puteți rezolva problema, atunci trimite ea la noi. Noi vom oferi solutie detaliata. Veți putea vizualiza progresul calculului și veți obține informații. Acest lucru vă va ajuta să obțineți nota de la profesorul dvs. în timp util! |
| Răspuns |
| $$ \lim_(x\la 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Exemplul 2 |
| Găsiți $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Soluţie |
|
Ca întotdeauna, mai întâi trebuie să cunoașteți tipul de incertitudine. Dacă este zero împărțit la zero, atunci acordăm atenție prezenței unui sinus: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Această incertitudine ne permite să folosim formula primei limite remarcabile, dar expresia de la numitor nu este egală cu argumentul sinusului? Prin urmare, formula nu poate fi aplicată „direct”. Este necesar să înmulțiți și să împărțiți fracția cu argumentul sinusului: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x ^3+2x)) = $$ Acum notăm proprietățile limitelor: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ A doua limită se potrivește exact formulei și este egală la unu: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ Înlocuim din nou $ x = 0 $ într-o fracție și obținem incertitudinea $ \frac(0)(0) $. Pentru a o elimina, este suficient să scoateți $ x $ din paranteze și să-l reduceți cu: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| Răspuns |
| $$ \lim_(x\la 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Exemplul 4 |
| Calculați $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Soluţie |
|
Să începem calculul cu înlocuirea $ x=0 $. Ca rezultat, obținem incertitudinea $ \frac(0)(0) $. Limita conține un sinus și o tangentă, care sugerează o posibilă desfășurare a situației folosind formula primei limite remarcabile. Să transformăm numărătorul și numitorul fracției într-o formulă și consecință: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Acum vedem că în numărător și numitor există expresii care se potrivesc formulei și consecințelor. Argumentul sinus și argumentul tangentei sunt aceleași pentru numitorii corespunzători $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| Răspuns |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
Articolul: „Prima limită remarcabilă, exemple de soluții” a vorbit despre cazuri în care este indicat să se folosească această formulă și consecințele ei.
Acest articol: „A doua limită remarcabilă” este dedicat dezvăluirii în limitele incertitudinilor de forma:
$ \bigg[\frac(\infty)(\infty)\bigg]^\infty $ și $ ^\infty $.
De asemenea, astfel de incertitudini pot fi relevate folosind logaritmul funcției exponențiale, dar aceasta este o altă metodă de soluție, care va fi tratată într-un alt articol.
Formula și consecințele
Formulă a doua limită remarcabilă se scrie astfel: $$ \lim_(x \to \infty) \bigg (1+\frac(1)(x)\bigg)^x = e, \text( where ) e \approx 2.718 $$
Rezultă din formulă consecințe, care sunt foarte convenabile de utilizat pentru rezolvarea exemplelor cu limite: $$ \lim_(x \to \infty) \bigg (1 + \frac(k)(x) \bigg)^x = e^k, \text( unde ) k \in \mathbb(R) $$ $$ \lim_(x \to \infty) \bigg (1 + \frac(1)(f(x)) \bigg)^(f(x)) = e $ $ $$ \lim_(x \to 0) \bigg (1 + x \bigg)^\frac(1)(x) = e $$
Este de remarcat faptul că a doua limită remarcabilă nu poate fi aplicată întotdeauna unei funcții exponențiale, ci numai în cazurile în care baza tinde spre unitate. Pentru a face acest lucru, mai întâi calculați mental limita bazei și apoi trageți concluzii. Toate acestea vor fi discutate în soluții de exemplu.
Exemple de soluții
Să ne uităm la exemple de soluții folosind formula directă și consecințele acesteia. Vom analiza și cazurile în care formula nu este necesară. Este suficient să scrieți doar un răspuns gata.
| Exemplul 1 |
| Găsiți limita $ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) $ |
| Soluţie |
|
Să substituim infinitul în limită și să ne uităm la incertitudinea: $$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) = \bigg (\frac (\infty)(\infty)\bigg)^\infty $$ Să găsim limita bazei: $$ \lim_(x\to\infty) \frac(x+4)(x+3)= \lim_(x\to\infty) \frac(x(1+\frac) (4)() x)))(x(1+\frac(3)(x))) = 1 $$ Am obținut o bază egală cu unu, ceea ce înseamnă că putem aplica deja a doua limită remarcabilă. Pentru a face acest lucru, să ajustăm baza funcției la formula scăzând și adăugând una: $$ \lim_(x\to\infty) \bigg(1 + \frac(x+4)(x+3) - 1 \bigg)^(x+3) = \lim_(x\to\infty) \ bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = $$ Să ne uităm la al doilea corolar și să scriem răspunsul: $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ Dacă nu vă puteți rezolva problema, trimiteți-ne-o. Vom oferi o soluție detaliată. Veți putea vizualiza progresul calculului și veți obține informații. Acest lucru vă va ajuta să obțineți nota de la profesorul dvs. în timp util! |
| Răspuns |
| $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ |
| Exemplul 4 |
| Rezolvați limita $ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) $ |
| Soluţie |
|
Găsim limita bazei și vedem că $ \lim_(x\to\infty) \frac(3x^2+4)(3x^2-2) = 1 $, ceea ce înseamnă că putem aplica a doua limită remarcabilă. Conform planului standard, adunăm și scădem unul din baza gradului: $$ \lim_(x\la \infty) \bigg (1+\frac(3x^2+4)(3x^2-2)-1 \bigg) ^(3x) = \lim_(x\to \infty ) \bigg (1+\frac(6)(3x^2-2) \bigg) ^(3x) = $$ Ajustăm fracția la formula notei a 2-a. limită: $$ = \lim_(x\la \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(3x) = $$ Acum, să ajustăm gradul. Puterea trebuie să conțină o fracție egală cu numitorul bazei $ \frac(3x^2-2)(6) $. Pentru a face acest lucru, înmulțiți și împărțiți gradul cu acesta și continuați să rezolvați: $$ = \lim_(x\la \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(\frac(3x^2-2) (6) \cdot \frac(6)(3x^2-2)\cdot 3x) = \lim_(x\to \infty) e^(\frac(18x)(3x^2-2)) = $$ Limita situată în puterea la $ e $ este egală cu: $ \lim_(x\to \infty) \frac(18x)(3x^2-2) = 0 $. Așadar, continuând soluția avem: |
| Răspuns |
| $$ \lim_(x\la \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) = 1 $$ |
Să examinăm cazurile în care problema este similară cu cea de-a doua limită remarcabilă, dar poate fi rezolvată fără ea.
În articolul: „A doua limită remarcabilă: exemple de soluții” au fost analizate formula, consecințele acesteia și au fost prezentate tipuri comune de probleme pe această temă.

