Second order curves on a plane are lines defined by equations in which the variable coordinates x And y are contained in the second degree. These include the ellipse, hyperbola and parabola.
The general form of the second order curve equation is as follows:
Where A, B, C, D, E, F- numbers and at least one of the coefficients A, B, C not equal to zero.
When solving problems with second-order curves, the canonical equations of the ellipse, hyperbola and parabola are most often considered. It is easy to move on to them from general equations; example 1 of problems with ellipses will be devoted to this.
Ellipse given by the canonical equation
Definition of an ellipse. An ellipse is the set of all points of the plane for which the sum of the distances to the points called foci is a constant value greater than the distance between the foci.
The focuses are indicated as in the figure below.
The canonical equation of an ellipse has the form:
Where a And b (a > b) - the lengths of the semi-axes, i.e., half the lengths of the segments cut off by the ellipse on the coordinate axes.
The straight line passing through the foci of the ellipse is its axis of symmetry. Another axis of symmetry of an ellipse is a straight line passing through the middle of a segment perpendicular to this segment. Dot ABOUT the intersection of these lines serves as the center of symmetry of the ellipse or simply the center of the ellipse.
The abscissa axis of the ellipse intersects at the points ( a, ABOUT) And (- a, ABOUT), and the ordinate axis is in points ( b, ABOUT) And (- b, ABOUT). These four points are called the vertices of the ellipse. The segment between the vertices of the ellipse on the x-axis is called its major axis, and on the ordinate axis - its minor axis. Their segments from the top to the center of the ellipse are called semi-axes.
If a = b, then the equation of the ellipse takes the form . This is the equation of a circle with radius a, and the circle is special case ellipse. An ellipse can be obtained from a circle of radius a, if you compress it into a/b times along the axis Oy .
Example 1. Check if a line given by a general equation is 
, ellipse.
Solution. We make transformations general equation. We use the transfer of the free term to the right side, the term-by-term division of the equation by the same number and the reduction of fractions:
Answer. The equation obtained as a result of the transformations is the canonical equation of the ellipse. Therefore, this line is an ellipse.
Example 2. Compose the canonical equation of an ellipse if its semi-axes are 5 and 4, respectively.
Solution. We look at the formula for the canonical equation of an ellipse and substitute: the semimajor axis is a= 5, the semiminor axis is b= 4 . We obtain the canonical equation of the ellipse:
Points and , indicated in green on the major axis, where
are called tricks.
called eccentricity ellipse.
Attitude b/a characterizes the “oblateness” of the ellipse. The smaller this ratio, the more the ellipse is elongated along the major axis. However, the degree of elongation of an ellipse is more often expressed through eccentricity, the formula for which is given above. For different ellipses, the eccentricity varies from 0 to 1, always remaining less than unity.
Example 3. Compose the canonical equation of the ellipse if the distance between the foci is 8 and the major axis is 10.
Solution. Let's make some simple conclusions:
If the major axis is equal to 10, then its half, i.e. the semi-axis a = 5 ,
If the distance between the foci is 8, then the number c of the focal coordinates is equal to 4.
We substitute and calculate:
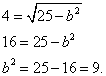
The result is the canonical equation of the ellipse:
Example 4. Compose the canonical equation of an ellipse if its major axis is 26 and its eccentricity is .
Solution. As follows from both the size of the major axis and the eccentricity equation, the semimajor axis of the ellipse a= 13. From the eccentricity equation we express the number c, needed to calculate the length of the minor semi-axis:
.
We calculate the square of the length of the minor semi-axis:
We compose the canonical equation of the ellipse:
Example 5. Determine the foci of the ellipse given by the canonical equation.
Solution. Find the number c, which determines the first coordinates of the ellipse's foci:
.
We get the focuses of the ellipse:
Example 6. The foci of the ellipse are located on the axis Ox symmetrically about the origin. Compose the canonical equation of the ellipse if:
1) the distance between the focuses is 30, and the major axis is 34
2) minor axis 24, and one of the focuses is at point (-5; 0)
3) eccentricity, and one of the foci is at point (6; 0)
Let's continue to solve ellipse problems together
If is an arbitrary point of the ellipse (indicated in green in the upper right part of the ellipse in the drawing) and is the distance to this point from the foci, then the formulas for the distances are as follows:
For each point belonging to the ellipse, the sum of the distances from the foci is a constant value equal to 2 a.
Lines defined by equations
are called headmistresses ellipse (in the drawing there are red lines along the edges).
From the two equations above it follows that for any point of the ellipse
,
where and are the distances of this point to the directrixes and .
Example 7. Given an ellipse. Write an equation for its directrixes.
Solution. We look at the directrix equation and find that we need to find the eccentricity of the ellipse, i.e. We have all the data for this. We calculate:
.
We obtain the equation of the directrixes of the ellipse:
Example 8. Compose the canonical equation of an ellipse if its foci are points and directrixes are lines.
Lectures on algebra and geometry. Semester 1.
Lecture 15. Ellipse.
Chapter 15. Ellipse.
clause 1. Basic definitions.
Definition. An ellipse is the GMT of a plane, the sum of the distances to two fixed points of the plane, called foci, is a constant value.
Definition. The distance from an arbitrary point M of the plane to the focus of the ellipse is called the focal radius of the point M.
Designations: 
– foci of the ellipse, 
– focal radii of point M.
By the definition of an ellipse, a point M is a point of an ellipse if and only if 
– constant value. This constant is usually denoted as 2a:
.
(1)
notice, that 
.
By definition of an ellipse, its foci are fixed points, so the distance between them is also a constant value for a given ellipse.
Definition. The distance between the foci of the ellipse is called the focal length.
Designation: 
.
From a triangle 
follows that 
, i.e.
.
Let us denote by b the number equal to 
, i.e.
.
(2)
Definition. Attitude
(3)
is called the eccentricity of the ellipse.
Let us introduce a coordinate system on this plane, which we will call canonical for the ellipse.
Definition. The axis on which the foci of the ellipse lie is called the focal axis.
Let's construct a canonical PDSC for the ellipse, see Fig. 2.
We select the focal axis as the abscissa axis, and draw the ordinate axis through the middle of the segment 
perpendicular to the focal axis.
Then the foci have coordinates 
,
.
clause 2. Canonical equation of an ellipse.
Theorem. In the canonical coordinate system for an ellipse, the equation of the ellipse has the form:
.
(4)
Proof. We carry out the proof in two stages. At the first stage, we will prove that the coordinates of any point lying on the ellipse satisfy equation (4). At the second stage we will prove that any solution to equation (4) gives the coordinates of a point lying on the ellipse. From here it will follow that equation (4) is satisfied by those and only those points of the coordinate plane that lie on the ellipse. From this and from the definition of the equation of a curve it will follow that equation (4) is an equation of an ellipse.
1) Let the point M(x, y) be a point of the ellipse, i.e. the sum of its focal radii is 2a:
.
Let's use the formula for the distance between two points on the coordinate plane and use this formula to find the focal radii of a given point M:
,
, from where we get:
Let's move one root to the right side of the equality and square it:
Reducing, we get:
We present similar ones, reduce by 4 and remove the radical:
.
Squaring
Open the brackets and shorten by 
:
where we get:
Using equality (2), we obtain:
.
Dividing the last equality by 
, we obtain equality (4), etc.
2) Let now a pair of numbers (x, y) satisfy equation (4) and let M(x, y) be the corresponding point on the coordinate plane Oxy.
Then from (4) it follows:
.
We substitute this equality into the expression for the focal radii of point M:
.
Here we used equality (2) and (3).
Thus, 
. Likewise, 
.
Now note that from equality (4) it follows that
or 
etc. 
, then the inequality follows:
.
From here it follows, in turn, that
or 
And
,
.
(5)
From equalities (5) it follows that 
, i.e. the point M(x, y) is a point of the ellipse, etc.
The theorem has been proven.
Definition. Equation (4) is called the canonical equation of the ellipse.
Definition. The canonical coordinate axes for an ellipse are called the principal axes of the ellipse.
Definition. The origin of the canonical coordinate system for an ellipse is called the center of the ellipse.
clause 3. Properties of the ellipse.
Theorem. (Properties of an ellipse.)
1. In the canonical coordinate system for an ellipse, everything
the points of the ellipse are in the rectangle
,
.
2. The points lie on
3. An ellipse is a curve that is symmetrical with respect to
their main axes.
4. The center of the ellipse is its center of symmetry.
Proof. 1, 2) Immediately follows from the canonical equation of the ellipse.
3, 4) Let M(x, y) be an arbitrary point of the ellipse. Then its coordinates satisfy equation (4). But then the coordinates of the points also satisfy equation (4), and, therefore, are points of the ellipse, from which the statements of the theorem follow.
The theorem has been proven.
Definition. The quantity 2a is called the major axis of the ellipse, the quantity a is called the semi-major axis of the ellipse.
Definition. The quantity 2b is called the minor axis of the ellipse, the quantity b is called the semiminor axis of the ellipse.
Definition. The points of intersection of an ellipse with its main axes are called the vertices of the ellipse.
Comment. An ellipse can be constructed as follows. On the plane, we “hammer a nail into the focal points” and fasten a thread length to them 
. Then we take a pencil and use it to stretch the thread. Then we move the pencil lead along the plane, making sure that the thread is taut.
From the definition of eccentricity it follows that
Let us fix the number a and direct the number c to zero. Then at 
,
And 
. In the limit we get
or 
– equation of a circle.
Let us now direct 
. Then 
,
and we see that in the limit the ellipse degenerates into a straight line segment 
in the notation of Figure 3.
clause 4. Parametric equations of the ellipse.
Theorem. Let 
– arbitrary real numbers. Then the system of equations
,
(6)
are parametric equations of an ellipse in the canonical coordinate system for the ellipse.
Proof. It is enough to prove that the system of equations (6) is equivalent to equation (4), i.e. they have the same set of solutions.
1) Let (x, y) be an arbitrary solution to system (6). Divide the first equation by a, the second by b, square both equations and add:
.
Those. any solution (x, y) of system (6) satisfies equation (4).
2) Conversely, let the pair (x, y) be a solution to equation (4), i.e.
.
From this equality it follows that the point with coordinates 
lies on a circle of unit radius with center at the origin, i.e. is a point on a trigonometric circle to which a certain angle corresponds 
:
From the definition of sine and cosine it immediately follows that
,
, Where 
, from which it follows that the pair (x, y) is a solution to system (6), etc.
The theorem has been proven.
Comment. An ellipse can be obtained as a result of uniform “compression” of a circle of radius a towards the abscissa axis.
Let 
– equation of a circle with center at the origin. “Compression” of a circle to the abscissa axis is nothing more than a transformation of the coordinate plane, carried out according to the following rule. For each point M(x, y) we associate a point on the same plane 
, Where 
,
– compression ratio.
With this transformation, each point on the circle “transitions” to another point on the plane, which has the same abscissa, but a smaller ordinate. Let's express the old ordinate of a point through the new one:
and substitute circles into the equation:
.
From here we get:
.
(7)
It follows from this that if before the “compression” transformation the point M(x, y) lay on the circle, i.e. its coordinates satisfied the equation of the circle, then after the “compression” transformation this point “transformed” into the point 
, whose coordinates satisfy the ellipse equation (7). If we want to obtain the equation of an ellipse with semiminor axisb, then we need to take the compression factor
.
clause 5. Tangent to an ellipse.
Theorem. Let 
– arbitrary point of the ellipse
.
Then the equation of the tangent to this ellipse at the point 
has the form:
.
(8)
Proof. It is enough to consider the case when the point of tangency lies in the first or second quarter of the coordinate plane: 
. The equation of the ellipse in the upper half-plane has the form:
.
(9)
Let's use the tangent equation to the graph of the function 
at the point 
:
Where 
– the value of the derivative of a given function at a point 
. The ellipse in the first quarter can be considered as a graph of function (8). Let's find its derivative and its value at the point of tangency:
,
. Here we took advantage of the fact that the tangent point 
is a point of the ellipse and therefore its coordinates satisfy the ellipse equation (9), i.e.
.
We substitute the found value of the derivative into the tangent equation (10):
,
where we get:
This implies:
Let's divide this equality by 
:
.
It remains to note that 
, because dot 
belongs to the ellipse and its coordinates satisfy its equation.
The tangent equation (8) is proved in a similar way at the point of tangency lying in the third or fourth quarter of the coordinate plane.
And finally, we can easily verify that equation (8) gives the tangent equation at the points 
,
:
or 
, And 
or 
.
The theorem has been proven.
clause 6. Mirror property of an ellipse.
Theorem. The tangent to the ellipse has equal angles with the focal radii of the point of tangency.
Let 
– point of contact, 
,
– focal radii of the tangent point, P and Q – projections of foci on the tangent drawn to the ellipse at the point 
.
The theorem states that
.
(11)
This equality can be interpreted as the equality of the angles of incidence and reflection of a ray of light from an ellipse released from its focus. This property is called the mirror property of the ellipse:
A ray of light released from the focus of the ellipse, after reflection from the mirror of the ellipse, passes through another focus of the ellipse.
Proof of the theorem. To prove the equality of angles (11), we prove the similarity of triangles 
And 
, in which the parties 
And 
will be similar. Since the triangles are right-angled, it is enough to prove the equality
An ellipse is the geometric locus of points on a plane, the sum of the distances from each of them to two given points F_1, and F_2 is a constant value (2a) greater than the distance (2c) between these given points(Fig. 3.36, a). This geometric definition expresses focal property of an ellipse.
Focal property of an ellipse
Points F_1 and F_2 are called the foci of the ellipse, the distance between them 2c=F_1F_2 is the focal length, the middle O of the segment F_1F_2 is the center of the ellipse, the number 2a is the length of the major axis of the ellipse (accordingly, the number a is the semi-major axis of the ellipse). The segments F_1M and F_2M connecting an arbitrary point M of the ellipse with its foci are called focal radii of point M. The segment connecting two points of an ellipse is called a chord of the ellipse.
The ratio e=\frac(c)(a) is called the eccentricity of the ellipse. From definition (2a>2c) it follows that 0\leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
Geometric definition of ellipse, expressing its focal property, is equivalent to its analytical definition - the line given by the canonical equation of the ellipse:
Indeed, let us introduce a rectangular coordinate system (Fig. 3.36c). We take the center O of the ellipse as the origin of the coordinate system; we take the straight line passing through the foci (focal axis or first axis of the ellipse) as the abscissa axis (the positive direction on it is from point F_1 to point F_2); let us take a straight line perpendicular to the focal axis and passing through the center of the ellipse (the second axis of the ellipse) as the ordinate axis (the direction on the ordinate axis is chosen so that the rectangular coordinate system Oxy is right).
Let's create an equation for the ellipse using its geometric definition, which expresses the focal property. In the selected coordinate system, we determine the coordinates of the foci F_1(-c,0),~F_2(c,0). For an arbitrary point M(x,y) belonging to the ellipse, we have:
\vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a.
Writing this equality in coordinate form, we get:
\sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a.
We move the second radical to the right side, square both sides of the equation and bring similar terms:
(x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt((x-c )^2+y^2)=4a^2-4cx.
Dividing by 4, we square both sides of the equation:
A^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2).
Having designated b=\sqrt(a^2-c^2)>0, we get b^2x^2+a^2y^2=a^2b^2. Dividing both sides by a^2b^2\ne0, we arrive at the canonical equation of the ellipse:
\frac(x^2)(a^2)+\frac(y^2)(b^2)=1.
Therefore, the chosen coordinate system is canonical.
If the foci of the ellipse coincide, then the ellipse is a circle (Fig. 3.36,6), since a=b. In this case, any rectangular coordinate system with origin at the point will be canonical O\equiv F_1\equiv F_2, and the equation x^2+y^2=a^2 is the equation of a circle with center at point O and radius equal to a.
By reasoning in reverse order, it can be shown that all points whose coordinates satisfy equation (3.49), and only they, belong to the geometric locus of points called an ellipse. In other words, the analytical definition of an ellipse is equivalent to its geometric definition, which expresses the focal property of the ellipse.
Directorial property of an ellipse
The directrixes of an ellipse are two straight lines running parallel to the ordinate axis of the canonical coordinate system at the same distance \frac(a^2)(c) from it. At c=0, when the ellipse is a circle, there are no directrixes (we can assume that the directrixes are at infinity).
Ellipse with eccentricity 0
In fact, for example, for focus F_2 and directrix d_2 (Fig. 3.37,6) the condition \frac(r_2)(\rho_2)=e can be written in coordinate form:
\sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\right)
Getting rid of irrationality and replacing e=\frac(c)(a),~a^2-c^2=b^2, we arrive at the canonical ellipse equation (3.49). Similar reasoning can be carried out for focus F_1 and director d_1\colon\frac(r_1)(\rho_1)=e.
Equation of an ellipse in a polar coordinate system
The equation of the ellipse in the polar coordinate system F_1r\varphi (Fig. 3.37, c and 3.37 (2)) has the form
R=\frac(p)(1-e\cdot\cos\varphi)
where p=\frac(b^2)(a) is the focal parameter of the ellipse.
In fact, let us choose the left focus F_1 of the ellipse as the pole of the polar coordinate system, and the ray F_1F_2 as the polar axis (Fig. 3.37, c). Then for an arbitrary point M(r,\varphi), according to the geometric definition (focal property) of an ellipse, we have r+MF_2=2a. We express the distance between points M(r,\varphi) and F_2(2c,0) (see paragraph 2 of remarks 2.8):
\begin(aligned)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(aligned)
Therefore, in coordinate form, the equation of the ellipse F_1M+F_2M=2a has the form
R+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a.
We isolate the radical, square both sides of the equation, divide by 4 and present similar terms:
R^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2.
Express the polar radius r and make the replacement e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a):
R=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1 -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi),
Q.E.D.
Geometric meaning of the coefficients in the ellipse equation
Let's find the intersection points of the ellipse (see Fig. 3.37a) with the coordinate axes (vertices of the ellipse). Substituting y=0 into the equation, we find the points of intersection of the ellipse with the abscissa axis (with the focal axis): x=\pm a. Therefore, the length of the segment of the focal axis contained inside the ellipse is equal to 2a. This segment, as noted above, is called the major axis of the ellipse, and the number a is the semi-major axis of the ellipse. Substituting x=0, we get y=\pm b. Therefore, the length of the segment of the second axis of the ellipse contained inside the ellipse is equal to 2b. This segment is called the minor axis of the ellipse, and the number b is the semiminor axis of the ellipse.
Really, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, and the equality b=a is obtained only in the case c=0, when the ellipse is a circle. Attitude k=\frac(b)(a)\leqslant1 is called the ellipse compression ratio.
Notes 3.9
1. The straight lines x=\pm a,~y=\pm b limit the main rectangle on the coordinate plane, inside of which there is an ellipse (see Fig. 3.37, a).
2. An ellipse can be defined as the locus of points obtained by compressing a circle to its diameter.
Indeed, let the equation of a circle in the rectangular coordinate system Oxy be x^2+y^2=a^2. When compressed to the x-axis with a coefficient of 0 \begin(cases)x"=x,\\y"=k\cdot y.\end(cases) Substituting circles x=x" and y=\frac(1)(k)y" into the equation, we obtain the equation for the coordinates of the image M"(x",y") of the point M(x,y) : (x")^2+(\left(\frac(1)(k)\cdot y"\right)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} since b=k\cdot a . This is the canonical equation of the ellipse. 3. The coordinate axes (of the canonical coordinate system) are the axes of symmetry of the ellipse (called the main axes of the ellipse), and its center is the center of symmetry. Indeed, if the point M(x,y) belongs to the ellipse . then the points M"(x,-y) and M""(-x,y), symmetrical to the point M relative to the coordinate axes, also belong to the same ellipse. 4. From the equation of the ellipse in the polar coordinate system r=\frac(p)(1-e\cos\varphi)(see Fig. 3.37, c), the geometric meaning of the focal parameter is clarified - this is half the length of the chord of the ellipse passing through its focus perpendicular to the focal axis ( r = p at \varphi=\frac(\pi)(2)). 5. Eccentricity e characterizes the shape of the ellipse, namely the difference between the ellipse and the circle. The larger e, the more elongated the ellipse, and the closer e is to zero, the closer the ellipse is to a circle (Fig. 3.38a). Indeed, taking into account that e=\frac(c)(a) and c^2=a^2-b^2 , we get E^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} where k is the ellipse compression ratio, 0 6. Equation \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 at a
7. Equation \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b defines an ellipse with center at point O"(x_0,y_0), the axes of which are parallel to the coordinate axes (Fig. 3.38, c). This equation is reduced to the canonical one using parallel translation (3.36). When a=b=R the equation (x-x_0)^2+(y-y_0)^2=R^2 describes a circle of radius R with center at point O"(x_0,y_0) . Parametric equation of ellipse in the canonical coordinate system has the form \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
Indeed, substituting these expressions into equation (3.49), we arrive at the main trigonometric identity \cos^2t+\sin^2t=1 . Example 3.20. Draw an ellipse \frac(x^2)(2^2)+\frac(y^2)(1^2)=1 in the canonical coordinate system Oxy. Find the semi-axes, focal length, eccentricity, compression ratio, focal parameter, directrix equations. Solution. Comparing the given equation with the canonical one, we determine the semi-axes: a=2 - semi-major axis, b=1 - semi-minor axis of the ellipse. We build the main rectangle with sides 2a=4,~2b=2 with the center at the origin (Fig. 3.39). Considering the symmetry of the ellipse, we fit it into the main rectangle. If necessary, determine the coordinates of some points of the ellipse. For example, substituting x=1 into the equation of the ellipse, we get \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Therefore, points with coordinates \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\right)- belong to the ellipse. Calculating the compression ratio k=\frac(b)(a)=\frac(1)(2); focal length 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); eccentricity e=\frac(c)(a)=\frac(\sqrt(3))(2); focal parameter p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). We compose the directrix equations: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)). An ellipse is the geometric locus of points on a plane, the sum of the distances from each of which to two given points F_1, and F_2 is a constant value (2a), greater than the distance (2c) between these given points (Fig. 3.36, a). This geometric definition expresses focal property of an ellipse. Points F_1 and F_2 are called the foci of the ellipse, the distance between them 2c=F_1F_2 is the focal length, the middle O of the segment F_1F_2 is the center of the ellipse, the number 2a is the length of the major axis of the ellipse (accordingly, the number a is the semi-major axis of the ellipse). The segments F_1M and F_2M connecting an arbitrary point M of the ellipse with its foci are called focal radii of point M. The segment connecting two points of an ellipse is called a chord of the ellipse. The ratio e=\frac(c)(a) is called the eccentricity of the ellipse. From definition (2a>2c) it follows that 0\leqslant e<1
. При e=0
, т.е. при c=0
, фокусы F_1
и F_2
, а также центр O
совпадают, и эллипс является окружностью радиуса a
(рис.3.36,6). Geometric definition of ellipse, expressing its focal property, is equivalent to its analytical definition - the line given by the canonical equation of the ellipse: Indeed, let us introduce a rectangular coordinate system (Fig. 3.36c). We take the center O of the ellipse as the origin of the coordinate system; we take the straight line passing through the foci (focal axis or first axis of the ellipse) as the abscissa axis (the positive direction on it is from point F_1 to point F_2); let us take a straight line perpendicular to the focal axis and passing through the center of the ellipse (the second axis of the ellipse) as the ordinate axis (the direction on the ordinate axis is chosen so that the rectangular coordinate system Oxy is right). Let's create an equation for the ellipse using its geometric definition, which expresses the focal property. In the selected coordinate system, we determine the coordinates of the foci F_1(-c,0),~F_2(c,0). For an arbitrary point M(x,y) belonging to the ellipse, we have: \vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a. Writing this equality in coordinate form, we get: \sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a. We move the second radical to the right side, square both sides of the equation and bring similar terms: (x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt((x-c )^2+y^2)=4a^2-4cx. Dividing by 4, we square both sides of the equation: a^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2). Having designated b=\sqrt(a^2-c^2)>0, we get b^2x^2+a^2y^2=a^2b^2. Dividing both sides by a^2b^2\ne0, we arrive at the canonical equation of the ellipse: \frac(x^2)(a^2)+\frac(y^2)(b^2)=1. Therefore, the chosen coordinate system is canonical. If the foci of the ellipse coincide, then the ellipse is a circle (Fig. 3.36,6), since a=b. In this case, any rectangular coordinate system with origin at the point will be canonical O\equiv F_1\equiv F_2, and the equation x^2+y^2=a^2 is the equation of a circle with center at point O and radius equal to a. Carrying out the reasoning in reverse order, it can be shown that all points whose coordinates satisfy equation (3.49), and only they, belong to the locus of points called an ellipse. In other words, the analytical definition of an ellipse is equivalent to its geometric definition, which expresses the focal property of the ellipse. The directrixes of an ellipse are two straight lines running parallel to the ordinate axis of the canonical coordinate system at the same distance \frac(a^2)(c) from it. At c=0, when the ellipse is a circle, there are no directrixes (we can assume that the directrixes are at infinity). Ellipse with eccentricity 0 In fact, for example, for focus F_2 and directrix d_2 (Fig. 3.37,6) the condition \frac(r_2)(\rho_2)=e can be written in coordinate form: \sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\right) Getting rid of irrationality and replacing e=\frac(c)(a),~a^2-c^2=b^2, we arrive at the canonical ellipse equation (3.49). Similar reasoning can be carried out for focus F_1 and director d_1\colon\frac(r_1)(\rho_1)=e. The equation of the ellipse in the polar coordinate system F_1r\varphi (Fig. 3.37, c and 3.37 (2)) has the form r=\frac(p)(1-e\cdot\cos\varphi) where p=\frac(b^2)(a) is the focal parameter of the ellipse. In fact, let us choose the left focus F_1 of the ellipse as the pole of the polar coordinate system, and the ray F_1F_2 as the polar axis (Fig. 3.37, c). Then for an arbitrary point M(r,\varphi), according to the geometric definition (focal property) of an ellipse, we have r+MF_2=2a. We express the distance between points M(r,\varphi) and F_2(2c,0) (see): \begin(aligned)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(aligned) Therefore, in coordinate form, the equation of the ellipse F_1M+F_2M=2a has the form r+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a. We isolate the radical, square both sides of the equation, divide by 4 and present similar terms: r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2. Express the polar radius r and make the replacement e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a): r=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1 -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi), Q.E.D. Let's find the intersection points of the ellipse (see Fig. 3.37a) with the coordinate axes (vertices of the ellipse). Substituting y=0 into the equation, we find the points of intersection of the ellipse with the abscissa axis (with the focal axis): x=\pm a. Therefore, the length of the segment of the focal axis contained inside the ellipse is equal to 2a. This segment, as noted above, is called the major axis of the ellipse, and the number a is the semi-major axis of the ellipse. Substituting x=0, we get y=\pm b. Therefore, the length of the segment of the second axis of the ellipse contained inside the ellipse is equal to 2b. This segment is called the minor axis of the ellipse, and the number b is the semiminor axis of the ellipse. Really, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, and the equality b=a is obtained only in the case c=0, when the ellipse is a circle. Attitude k=\frac(b)(a)\leqslant1 is called the ellipse compression ratio. Notes 3.9 1. The straight lines x=\pm a,~y=\pm b limit the main rectangle on the coordinate plane, inside of which there is an ellipse (see Fig. 3.37, a). 2. An ellipse can be defined as the locus of points obtained by compressing a circle to its diameter. Indeed, let the equation of a circle in the rectangular coordinate system Oxy be x^2+y^2=a^2. When compressed to the x-axis with a coefficient of 0 \begin(cases)x"=x,\\y"=k\cdot y.\end(cases) Substituting circles x=x" and y=\frac(1)(k)y" into the equation, we obtain the equation for the coordinates of the image M"(x",y") of the point M(x,y) : (x")^2+(\left(\frac(1)(k)\cdot y"\right)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} since b=k\cdot a . This is the canonical equation of the ellipse. 3. The coordinate axes (of the canonical coordinate system) are the axes of symmetry of the ellipse (called the main axes of the ellipse), and its center is the center of symmetry. Indeed, if the point M(x,y) belongs to the ellipse . then the points M"(x,-y) and M""(-x,y), symmetrical to the point M relative to the coordinate axes, also belong to the same ellipse. 4. From the equation of the ellipse in the polar coordinate system r=\frac(p)(1-e\cos\varphi)(see Fig. 3.37, c), the geometric meaning of the focal parameter is clarified - this is half the length of the chord of the ellipse passing through its focus perpendicular to the focal axis (r=p at \varphi=\frac(\pi)(2)). 5. Eccentricity e characterizes the shape of the ellipse, namely the difference between the ellipse and the circle. The larger e, the more elongated the ellipse, and the closer e is to zero, the closer the ellipse is to a circle (Fig. 3.38a). Indeed, taking into account that e=\frac(c)(a) and c^2=a^2-b^2 , we get e^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} where k is the ellipse compression ratio, 0 6. Equation \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 at a 7. Equation \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b defines an ellipse with center at point O"(x_0,y_0), the axes of which are parallel to the coordinate axes (Fig. 3.38, c). This equation is reduced to the canonical one using parallel translation (3.36). When a=b=R the equation (x-x_0)^2+(y-y_0)^2=R^2 describes a circle of radius R with center at point O"(x_0,y_0) . Parametric equation of ellipse in the canonical coordinate system has the form \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
Indeed, substituting these expressions into equation (3.49), we arrive at the main trigonometric identity \cos^2t+\sin^2t=1. Example 3.20. Draw an ellipse \frac(x^2)(2^2)+\frac(y^2)(1^2)=1 in the canonical coordinate system Oxy. Find the semi-axes, focal length, eccentricity, compression ratio, focal parameter, directrix equations. Solution. Comparing the given equation with the canonical one, we determine the semi-axes: a=2 - semi-major axis, b=1 - semi-minor axis of the ellipse. We build the main rectangle with sides 2a=4,~2b=2 with the center at the origin (Fig. 3.39). Considering the symmetry of the ellipse, we fit it into the main rectangle. If necessary, determine the coordinates of some points of the ellipse. For example, substituting x=1 into the equation of the ellipse, we get \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Therefore, points with coordinates \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\right)- belong to the ellipse. Calculating the compression ratio k=\frac(b)(a)=\frac(1)(2); focal length 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); eccentricity e=\frac(c)(a)=\frac(\sqrt(3))(2); focal parameter p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). We compose the directrix equations: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)).Parametric equation of ellipse
To perform calculations, you must enable ActiveX controls!
Focal property of an ellipse
Directorial property of an ellipse
Equation of an ellipse in a polar coordinate system
Geometric meaning of the coefficients in the ellipse equation
Parametric equation of ellipse