home Secrets of medicine Projections onto coordinate axes. Projection of force on the axis

Projections onto coordinate axes. Projection of force on the axis

Projection vector onto an axis is a vector that is obtained by multiplying the scalar projection of a vector onto this axis and the unit vector of this axis. For example, if a x – scalar projection vector A to the X axis, then a x i- its vector projection onto this axis.

Let's denote vector projection the same as the vector itself, but with the index of the axis on which the vector is projected. So, the vector projection of the vector A on the X axis we denote A x ( fat a letter denoting a vector and a subscript of the axis name) or (a non-bold letter denoting a vector, but with an arrow at the top (!) and a subscript of the axis name).

Scalar projection vector per axis is called number, absolute value which is equal to the length of the axis segment (on the selected scale) enclosed between the projections of the start point and the end point of the vector. Usually instead of the expression scalar projection they simply say - projection. The projection is denoted by the same letter as the projected vector (in normal, non-bold writing), with a lower index (as a rule) of the name of the axis on which this vector is projected. For example, if a vector is projected onto the X axis A, then its projection is denoted by a x. When projecting the same vector onto another axis, if the axis is Y, its projection will be denoted a y.

To calculate the projection vector on an axis (for example, the X axis), it is necessary to subtract the coordinate of the starting point from the coordinate of its end point, that is
a x = x k − x n.
The projection of a vector onto an axis is a number. Moreover, the projection can be positive if the value x k greater than the value xn,

negative if the value x k is less than the value x n

and equal to zero if x k equals x n.

The projection of a vector onto an axis can also be found by knowing the modulus of the vector and the angle it makes with this axis.

From the figure it is clear that a x = a Cos α

that is, the projection of the vector onto the axis is equal to the product of the modulus of the vector and the cosine of the angle between the direction of the axis and vector direction. If the angle is acute, then
Cos α > 0 and a x > 0, and, if obtuse, then the cosine of the obtuse angle is negative, and the projection of the vector onto the axis will also be negative.

Angles measured from the axis counterclockwise are considered positive, and angles measured along the axis are negative. However, since cosine is an even function, that is, Cos α = Cos (− α), when calculating projections, angles can be counted both clockwise and counterclockwise.

To find the projection of a vector onto an axis, the modulus of this vector must be multiplied by the cosine of the angle between the direction of the axis and the direction of the vector.

Vector coordinates are the coefficients of the only possible linear combination of basis vectors in the selected coordinate system, equal to this vector.

where are the coordinates of the vector.

Scalar product vectors

Scalar product of vectors[- in finite-dimensional vector space is defined as the sum of the products of identical components being multiplied vectors.

For example, S.p.v. a = (a 1 , ..., a n) And b = (b 1 , ..., b n):

(a , b ) = a 1 b 1 + a 2 b 2 + ... + a n b n

§ 3. Projections of a vector on the coordinate axes

1. Finding projections geometrically.

Vector
- projection of the vector onto the axis OX
- projection of the vector onto the axis OY

Definition 1. Vector projection on any coordinate axis is a number taken with a plus or minus sign, corresponding to the length of the segment located between the bases of the perpendiculars dropped from the beginning and end of the vector to the coordinate axis.

The projection sign is defined as follows. If, when moving along the coordinate axis, there is a movement from the projection point of the beginning of the vector to the projection point of the end of the vector in the positive direction of the axis, then the projection of the vector is considered positive. If it is opposite to the axis, then the projection is considered negative.

The figure shows that if the vector is oriented somehow opposite to the coordinate axis, then its projection onto this axis is negative. If a vector is oriented somehow in the positive direction of the coordinate axis, then its projection onto this axis is positive.

If a vector is perpendicular to the coordinate axis, then its projection onto this axis is zero.
If a vector is codirectional with an axis, then its projection onto this axis is equal to the absolute value of the vector.
If a vector is directed oppositely to the coordinate axis, then its projection onto this axis is equal in absolute value to the absolute value of the vector taken with a minus sign.

2. Most general definition projections.

From a right triangle ABD: .

Definition 2. Vector projection on any coordinate axis is a number equal to the product of the modulus of the vector and the cosine of the angle formed by the vector with the positive direction of the coordinate axis.

The sign of the projection is determined by the sign of the cosine of the angle formed by the vector with the positive axis direction.
If the angle is acute, then the cosine has positive sign, and projections are positive. For obtuse angles, the cosine has a negative sign, so in such cases the projections onto the axis are negative.
- therefore, for vectors perpendicular to the axis, the projection is zero.

A vector description of movement is useful, since in one drawing you can always depict many different vectors and get a visual “picture” of movement before your eyes. However, using a ruler and a protractor every time to perform operations with vectors is very labor-intensive. Therefore, these actions are reduced to actions with positive and negative numbers - projections of vectors.

Projection of the vector onto the axis called a scalar quantity equal to the product of the modulus of the projected vector and the cosine of the angle between the directions of the vector and the selected coordinate axis.

The left drawing shows a displacement vector, the module of which is 50 km, and its direction forms obtuse angle 150° with the direction of the X axis. Using the definition, we find the projection of the displacement on the X axis:

sx = s cos(α) = 50 km cos(150°) = –43 km

Since the angle between the axes is 90°, it is easy to calculate that the direction of movement forms an acute angle of 60° with the direction of the Y axis. Using the definition, we find the projection of displacement on the Y axis:

sy = s cos(β) = 50 km cos(60°) = +25 km

As you can see, if the direction of the vector forms an acute angle with the direction of the axis, the projection is positive; if the direction of the vector forms an obtuse angle with the direction of the axis, the projection is negative.

The right drawing shows a velocity vector, the module of which is 5 m/s, and the direction forms an angle of 30° with the direction of the X axis. Let's find the projections:

υx = υ · cos(α) = 5 m/s · cos( 30°) = +4.3 m/s
υy = υ · cos(β) = 5 m/s · cos( 120°) = –2.5 m/s

It is much easier to find projections of vectors on axes if the projected vectors are parallel or perpendicular to the selected axes. Please note that for the case of parallelism, two options are possible: the vector is co-directional to the axis and the vector is opposite to the axis, and for the case of perpendicularity there is only one option.

The projection of a vector perpendicular to the axis is always zero (see sy and ay in the left drawing, and sx and υx in the right drawing). Indeed, for a vector perpendicular to the axis, the angle between it and the axis is 90°, so the cosine is zero, which means the projection is zero.

The projection of a vector codirectional with the axis is positive and equal to its absolute value, for example, sx = +s (see left drawing). Indeed, for a vector codirectional with the axis, the angle between it and the axis is zero, and its cosine is “+1”, that is, the projection is equal to the length of the vector: sx = x – xo = +s .

The projection of the vector opposite to the axis is negative and equal to its module taken with a minus sign, for example, sy = –s (see the right drawing). Indeed, for a vector opposite to the axis, the angle between it and the axis is 180°, and its cosine is “–1”, that is, the projection is equal to the length of the vector taken with a negative sign: sy = y – yo = –s .

The right-hand sides of both drawings show other cases where the vectors are parallel to one of the coordinate axes and perpendicular to the other. We invite you to make sure for yourself that in these cases, too, the rules formulated in the previous paragraphs are followed.

Introduction…………………………………………………………………………………3

1. Value of vector and scalar…………………………………….4

2. Definition of projection, axis and coordinate of a point………………...5

3. Projection of the vector onto the axis………………………………………………………...6

4. Basic formula of vector algebra……………………………..8

5. Calculation of the modulus of a vector from its projections…………………...9

Conclusion………………………………………………………………………………...11

Literature………………………………………………………………………………...12

Introduction:

Physics is inextricably linked with mathematics. Mathematics gives physics the means and techniques for a general and precise expression of the relationship between physical quantities that are discovered as a result of experiment or theoretical research. After all, the main method of research in physics is experimental. This means that a scientist reveals calculations using measurements. Denotes the relationship between various physical quantities. Then, everything is translated into the language of mathematics. Formed mathematical model. Physics is a science that studies the simplest and at the same time the most general patterns. The task of physics is to create in our minds a picture of the physical world that most fully reflects its properties and ensures such relationships between the elements of the model that exist between the elements.

So, physics creates a model of the world around us and studies its properties. But any model is limited. When creating models of a particular phenomenon, only properties and connections that are essential for a given range of phenomena are taken into account. This is the art of a scientist - to choose the main thing from all the diversity.

Physical models are mathematical, but mathematics is not their basis. Quantitative relationships between physical quantities are determined as a result of measurements, observations and experimental research and are only expressed in the language of mathematics. However, there is no other language for constructing physical theories.

1. Meaning of vector and scalar.

In physics and mathematics, a vector is a quantity that is characterized by its numerical value and direction. In physics, there are many important quantities that are vectors, for example, force, position, speed, acceleration, torque, momentum, electric and magnetic field strength. They can be contrasted with other quantities such as mass, volume, pressure, temperature and density, which can be described by an ordinary number, and are called " scalars".

They are written either in regular font letters or in numbers (a, b, t, G, 5, −7....). Scalar quantities can be positive or negative. At the same time, some objects of study may have such properties that full description For which knowledge of only a numerical measure turns out to be insufficient, it is also necessary to characterize these properties by direction in space. Such properties are characterized by vector quantities (vectors). Vectors, unlike scalars, are denoted by bold letters: a, b, g, F, C....
Often a vector is denoted by a letter in regular (non-bold) font, but with an arrow above it:

In addition, a vector is often denoted by a pair of letters (usually capitalized), with the first letter indicating the beginning of the vector and the second its end.

The modulus of a vector, that is, the length of a directed straight line segment, is denoted by the same letters as the vector itself, but in normal (not bold) writing and without an arrow above them, or in exactly the same way as a vector (that is, in bold or regular, but with arrow), but then the vector designation is enclosed in vertical dashes.
A vector is a complex object that is simultaneously characterized by both magnitude and direction.

There are also no positive and negative vectors. But vectors can be equal to each other. This is when, for example, a and b have the same modules and are directed in the same direction. In this case, the notation is true a= b. It should also be borne in mind that the vector symbol may be preceded by a minus sign, for example - c, however, this sign symbolically indicates that the vector -c has the same module as the vector c, but is directed in the opposite direction.

Vector -c is called the opposite (or inverse) of vector c.
In physics, each vector is filled with specific content, and when comparing vectors of the same type (for example, forces), the points of their application can also be significant.

2. Determination of the projection, axis and coordinate of the point.

Axis- This is a straight line that is given some direction.
An axis is designated by some letter: X, Y, Z, s, t... Usually a point is selected (arbitrarily) on the axis, which is called the origin and, as a rule, is designated by the letter O. From this point the distances to other points of interest to us are measured.

Projection of a point on an axis is the base of a perpendicular drawn from this point onto a given axis. That is, the projection of a point onto the axis is a point.

Point coordinate on a given axis is a number whose absolute value is equal to the length of the axis segment (on the selected scale) contained between the origin of the axis and the projection of the point onto this axis. This number is taken with a plus sign if the projection of the point is located in the direction of the axis from its origin and with a minus sign if in the opposite direction.

3. Projection of the vector onto the axis.

The projection of a vector onto an axis is a vector that is obtained by multiplying the scalar projection of a vector onto this axis and the unit vector of this axis. For example, if a x is the scalar projection of vector a onto the X axis, then a x ·i is its vector projection onto this axis.

Let us denote the vector projection in the same way as the vector itself, but with the index of the axis on which the vector is projected. Thus, we denote the vector projection of vector a onto the X axis as a x (a bold letter denoting the vector and the subscript of the axis name) or

(a low-bold letter denoting a vector, but with an arrow at the top (!) and a subscript for the axis name).

Scalar projection vector per axis is called number, the absolute value of which is equal to the length of the axis segment (on the selected scale) enclosed between the projections of the start point and the end point of the vector. Usually instead of the expression scalar projection they simply say - projection. The projection is denoted by the same letter as the projected vector (in normal, non-bold writing), with a lower index (as a rule) of the name of the axis on which this vector is projected. For example, if a vector is projected onto the X axis A, then its projection is denoted by a x. When projecting the same vector onto another axis, if the axis is Y, its projection will be denoted a y.

To calculate the projection vector on an axis (for example, the X axis), it is necessary to subtract the coordinate of the starting point from the coordinate of its end point, that is

a x = x k − x n.

The projection of a vector onto an axis is a number. Moreover, the projection can be positive if the value x k is greater than the value x n,

negative if the value x k is less than the value x n

and equal to zero if x k equals x n.

The projection of a vector onto an axis can also be found by knowing the modulus of the vector and the angle it makes with this axis.

From the figure it is clear that a x = a Cos α

That is, the projection of the vector onto the axis is equal to the product of the modulus of the vector and the cosine of the angle between the direction of the axis and vector direction. If the angle is acute, then
Cos α > 0 and a x > 0, and, if obtuse, then the cosine of the obtuse angle is negative, and the projection of the vector onto the axis will also be negative.

To find the projection of a vector onto an axis, the modulus of this vector must be multiplied by the cosine of the angle between the direction of the axis and the direction of the vector.

4. Basic formula of vector algebra.

Let's project vector a on the X and Y axes of the rectangular coordinate system. Let's find the vector projections of vector a on these axes:

a x = a x ·i, and y = a y ·j.

But in accordance with the rule of vector addition

a = a x + a y.

a = a x i + a y j.

Thus, we expressed a vector in terms of its projections and vectors of the rectangular coordinate system (or in terms of its vector projections).

Vector projections a x and a y are called components or components of the vector a. The operation we performed is called the decomposition of a vector along the axes of a rectangular coordinate system.

If the vector is given in space, then

a = a x i + a y j + a z k.

This formula is called the basic formula of vector algebra. Of course, it can be written like this.

There will also be problems for you to solve on your own, to which you can see the answers.

Vector concept

Before you learn everything about vectors and operations on them, get ready to solve a simple problem. There is a vector of your entrepreneurship and a vector of your innovative abilities. The vector of entrepreneurship leads you to Goal 1, and the vector of innovative abilities leads you to Goal 2. The rules of the game are such that you cannot move along the directions of these two vectors at once and achieve two goals at once. Vectors interact, or, speaking in mathematical language, some operation is performed on vectors. The result of this operation is the “Result” vector, which leads you to Goal 3.

Now tell me: the result of which operation on the vectors “Entrepreneurship” and “Innovative abilities” is the vector “Result”? If you can't tell right away, don't be discouraged. As you progress through this lesson, you will be able to answer this question.

As we have already seen above, the vector necessarily comes from a certain point A in a straight line to some point B. Therefore, each vector has not only numeric value- length, but also physical and geometric - directionality. From this comes the first, simplest definition of a vector. So, a vector is a directed segment coming from a point A to the point B. It is designated as follows: .

And to begin various operations with vectors , we need to get acquainted with one more definition of a vector.

A vector is a type of representation of a point that needs to be reached from some starting point. For example, a three-dimensional vector is usually written as (x, y, z) . In very simple terms, these numbers mean how far you need to walk in three different directions to get to a point.

Let a vector be given. Wherein x = 3 (right hand points to the right), y = 1 (left hand points forward) z = 5 (under the point there is a staircase leading up). Using these data, you will find a point by walking 3 meters in the direction indicated right hand, then 1 meter in the direction indicated by your left hand, and then a ladder awaits you and, rising 5 meters, you will finally find yourself at the end point.

All other terms are clarifications of the explanation presented above, necessary for various operations on vectors, that is, solving practical problems. Let's go through these more rigorous definitions, focusing on typical vector problems.

Physical examples vector quantities can be the displacement of a material point moving in space, the speed and acceleration of this point, as well as the force acting on it.

Geometric vector presented in two-dimensional and three-dimensional space in the form directional segment. This is a segment that has a beginning and an end.

If A- the beginning of the vector, and B- its end, then the vector is denoted by the symbol or one lowercase letter . In the figure, the end of the vector is indicated by an arrow (Fig. 1)

Length(or module) of a geometric vector is the length of the segment generating it

The two vectors are called equal , if they can be combined (if the directions coincide) by parallel transfer, i.e. if they are parallel, directed in the same direction and have equal lengths.

In physics it is often considered pinned vectors, specified by the point of application, length and direction. If the point of application of the vector does not matter, then it can be transferred, maintaining its length and direction, to any point in space. In this case, the vector is called free. We will agree to consider only free vectors.

Linear operations on geometric vectors

Multiplying a vector by a number

Product of a vector per number is a vector that is obtained from a vector by stretching (at ) or compressing (at ) by a factor, and the direction of the vector remains the same if , and changes to the opposite if . (Fig. 2)

From the definition it follows that the vectors and = are always located on one or parallel lines. Such vectors are called collinear. (We can also say that these vectors are parallel, but in vector algebra it is customary to say “collinear.”) The converse is also true: if the vectors are collinear, then they are related by the relation

Consequently, equality (1) expresses the condition of collinearity of two vectors.

Addition and subtraction of vectors

When adding vectors you need to know that amount vectors and is called a vector, the beginning of which coincides with the beginning of the vector, and the end with the end of the vector, provided that the beginning of the vector is attached to the end of the vector. (Fig. 3)

This definition can be distributed over any finite number of vectors. Let them be given in space n free vectors. When adding several vectors, their sum is taken to be the closing vector, the beginning of which coincides with the beginning of the first vector, and the end with the end of the last vector. That is, if you attach the beginning of the vector to the end of the vector, and the beginning of the vector to the end of the vector, etc. and, finally, to the end of the vector - the beginning of the vector, then the sum of these vectors is the closing vector , the beginning of which coincides with the beginning of the first vector, and the end - with the end of the last vector. (Fig. 4)

The terms are called components of the vector, and the formulated rule is polygon rule. This polygon may not be flat.

When a vector is multiplied by the number -1, the opposite vector is obtained. The vectors and have the same lengths and opposite directions. Their sum gives zero vector, whose length is zero. The direction of the zero vector is not defined.

In vector algebra, there is no need to consider the subtraction operation separately: subtracting a vector from a vector means adding the opposite vector to the vector, i.e.

Example 1. Simplify the expression:

that is, vectors can be added and multiplied by numbers in the same way as polynomials (in particular, also problems on simplifying expressions). Typically, the need to simplify linearly similar expressions with vectors arises before calculating the products of vectors.

Example 2. Vectors and serve as diagonals of the parallelogram ABCD (Fig. 4a). Express through and the vectors , , and , which are the sides of this parallelogram.

Solution. The point of intersection of the diagonals of a parallelogram bisects each diagonal. We find the lengths of the vectors required in the problem statement either as half the sums of the vectors that form a triangle with the required ones, or as half the differences (depending on the direction of the vector serving as the diagonal), or, as in the latter case, half the sum taken with a minus sign. The result is the vectors required in the problem statement:

There is every reason to believe that you have now correctly answered the question about the vectors “Entrepreneurship” and “Innovative abilities” at the beginning of this lesson. Correct answer: an addition operation is performed on these vectors.

Solve vector problems yourself and then look at the solutions

How to find the length of the sum of vectors?

This task occupies a special place in operations with vectors, since it involves the use trigonometric properties. Let's say you come across a task like the following:

The vector lengths are given and the length of the sum of these vectors. Find the length of the difference between these vectors.

Solutions to this and other similar problems and explanations of how to solve them are in the lesson " Vector addition: length of the sum of vectors and the cosine theorem ".

And you can check the solution to such problems at Online calculator "Unknown side of a triangle (vector addition and cosine theorem)" .

Where are the products of vectors?

Vector-vector products are not linear operations and are considered separately. And we have lessons "Scalar product of vectors" and "Vector and mixed products of vectors".

Projection of a vector onto an axis

The projection of a vector onto an axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:

As is known, the projection of a point A on the straight line (plane) is the base of the perpendicular dropped from this point onto the straight line (plane).

Let be an arbitrary vector (Fig. 5), and and be the projections of its origin (points A) and end (points B) per axis l. (To construct a projection of a point A) draw a straight line through the point A a plane perpendicular to a straight line. The intersection of the line and the plane will determine the required projection.

Vector component on the l axis is called such a vector lying on this axis, the beginning of which coincides with the projection of the beginning, and the end with the projection of the end of the vector.

Projection of the vector onto the axis l called number

equal to the length of the component vector on this axis, taken with a plus sign if the direction of the components coincides with the direction of the axis l, and with a minus sign if these directions are opposite.

Basic properties of vector projections onto an axis:

1. Projections of equal vectors onto the same axis are equal to each other.

2. When a vector is multiplied by a number, its projection is multiplied by the same number.

3. The projection of the sum of vectors onto any axis is equal to the sum of the projections of the summands of the vectors onto the same axis.

4. The projection of the vector onto the axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:

Solution. Let's project vectors onto the axis l as defined in the theoretical background above. From Fig. 5a it is obvious that the projection of the sum of vectors is equal to the sum of the projections of vectors. We calculate these projections:

We find the final projection of the sum of vectors:

Relationship between a vector and a rectangular Cartesian coordinate system in space

Getting to know rectangular Cartesian coordinate system in space took place in the corresponding lesson, it is advisable to open it in a new window.

In an ordered system of coordinate axes 0xyz axis Ox called x-axis, axis 0y – y-axis, and axis 0z – axis applicate.

With an arbitrary point M space connect vector

called radius vector points M and project it onto each of the coordinate axes. Let us denote the magnitudes of the corresponding projections:

Numbers x, y, z are called coordinates of point M, respectively abscissa, ordinate And applicate, and are written as an ordered point of numbers: M(x;y;z)(Fig. 6).

A vector of unit length whose direction coincides with the direction of the axis is called unit vector(or ortom) axes. Let us denote by

Accordingly, the unit vectors of the coordinate axes Ox, Oy, Oz

Theorem. Any vector can be expanded into unit vectors of coordinate axes:

(2)

Equality (2) is called the expansion of the vector along the coordinate axes. The coefficients of this expansion are the projections of the vector onto the coordinate axes. Thus, the coefficients of expansion (2) of the vector along the coordinate axes are the coordinates of the vector.

After choosing a certain coordinate system in space, the vector and the triplet of its coordinates uniquely determine each other, so the vector can be written in the form

Representations of the vector in the form (2) and (3) are identical.

Condition for collinearity of vectors in coordinates

As we have already noted, vectors are called collinear if they are related by the relation

Let the vectors be given . These vectors are collinear if the coordinates of the vectors are related by the relation

that is, the coordinates of the vectors are proportional.

Example 6. Vectors are given . Are these vectors collinear?

Solution. Let's find out the relationship between the coordinates of these vectors:

The coordinates of the vectors are proportional, therefore, the vectors are collinear, or, what is the same, parallel.

Vector length and direction cosines

Due to the mutual perpendicularity of the coordinate axes, the length of the vector

equal to the length of the diagonal rectangular parallelepiped, built on vectors

and is expressed by the equality

(4)

A vector is completely defined by specifying two points (start and end), so the coordinates of the vector can be expressed in terms of the coordinates of these points.

Let, in a given coordinate system, the origin of the vector be at the point

and the end is at the point

From equality

Follows that

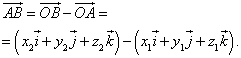
or in coordinate form

Hence, vector coordinates are equal to the differences between the same coordinates of the end and beginning of the vector . Formula (4) in this case will take the form

The direction of the vector is determined direction cosines . These are the cosines of the angles that the vector makes with the axes Ox, Oy And Oz. Let us denote these angles accordingly α , β And γ . Then the cosines of these angles can be found using the formulas

The direction cosines of a vector are also the coordinates of the vector of that vector and thus the vector of the vector