Incomplete quadratic equations are a special case of second-order equalities. It is necessary to be able to solve these equations, since they are often found not only in mathematical, but also in physical problems. This article is devoted to methods for solving them.
Quadratic equations: complete and incomplete
Before examining methods for solving incomplete quadratic equations, we should consider what they are.
The picture below shows general form second-order equalities, which are so called because of the maximum value of the degree of the variable (it is equal to 2) contained in them.
Where a, b and c are numbers (coefficients). An incomplete equation is obtained when one of these coefficients becomes equal to zero (with the exception of the number a, since if it becomes zero, the equation will no longer be quadratic). Since there are only three possible combinations of zero coefficients, the following types of incomplete second-order equalities are distinguished:
- Only b=0. Then the equation is transformed to the form a*x 2 + c = 0. It is called a pure or simple incomplete equality of quadratic type.
- Only c=0. Then we get the form: a*x 2 + b*x = 0. It is called a mixed incomplete quadratic equation.
- Finally, if b=0 and c=0, then we have the expression a*x 2 =0.
The last type of incomplete equation is not considered in any mathematical course, since its solution is obvious and the only possible one: x=0.
Is it possible to solve incomplete equations using a discriminant formula?
Yes, you can, since this method is universal for any second-order expressions. However, incomplete quadratic equations are already encountered in the 8th grade of school, and they begin to be studied earlier than complete equalities of this type, for which a formula with a discriminant is already given. In addition, the type of equalities under consideration is simple enough to apply universal formulas to them and perform a number of unnecessary calculations.
Let's consider simple and understandable ways to solve incomplete second-order equations.
Solving a simple incomplete equation
Scheme of its solution in general case is presented in the figure below.

Let us explain in more detail each step marked on it. The first step is to bring the equation to the form indicated at the beginning of this diagram. The condition of the problem can be composed in such a way that the original equality will contain more than two terms. All of them must be simplified (multiplied, added and subtracted) to the form of pure incomplete equality.
After this, the free term c is transferred to the right side of the equality and divided by the coefficient a. To obtain the unknowns x, all that remains is to take Square root from the ratio -c/a, but we must not forget and take into account that it can be either with a minus sign or with a positive sign.
What follows from the formula presented in the figure? Firstly, there are always 2 roots of a pure incomplete quadratic equality, while they are both equal in modulus, but different in sign. Secondly, if the numbers c and a have the same sign, then the roots of x will be imaginary; if c and a are of different signs, then two real solutions are obtained.
To solve a quadratic equation for which c = 0, you should take the same first step as in the case of determining the roots of a pure incomplete equality, that is, bring it to a form with two terms: one of them must contain x 2, and the other x. Then, you should apply the factorization method, that is, decompose left side equalities by factors. Unlike the full equation, this is very easy to do, since one of the factors will always be x. The above can be written as a formula:
This equality has a solution if each of its factors is zero. The result of calculating the roots is shown in the figure below.

Thus, the roots of this type of incomplete equation will always be real numbers, with one of them being zero. The sign of the second root is determined by the ratio of non-zero coefficients b/a.
Examples of math problems

Now we give visual examples of quadratic incomplete equations with solutions.
Example 1. Find the roots of the equality 135-(2x + 3) (2x - 3) = 0. Open the brackets and get: 135-4*x 2 +9=0. Note that terms containing x to the first power have been canceled. Carrying out the transfer of free terms to the right side and dividing them by -4, we get: x 2 = 36. This gives us two roots: 6 and -6.
Example 2. 23*(x 2 -2)=34*x-46. As in the first case, we open the brackets and move all the terms to the left side. We have: 23*x 2 -46-34*x+46=0. Now we reduce the free terms and factor the sum, we get: x*(23*x-34)=0. It follows that x=0 and x = 34/23≈1.47826.
Solving the examples showed that the algorithm for finding the roots of any type of incomplete second-order equation is quite simple, so there is no point in memorizing the formulas presented in the figures above.
Example of a physics problem
Many schoolchildren have heard from their physics teacher that Galileo Galilei in the 17th century conducted experiments to calculate the acceleration of gravity by dropping various bodies from the tower in Pisa. This will seem curious to many, but there is not a single historical evidence that the scientist actually conducted such experiments. However, in the same 17th century, they were performed by another Italian.
Giovanni Riccioli is an astronomer and Jesuit who was able to actually calculate the acceleration of a free fall by dropping clay balls from the height of the Asinelli Tower, located in the city of Bologna. Riccioli obtained an acceleration value of 9.6 m/s 2 (the modern value is 9.81 m/s 2 ). Knowing this number, it is necessary to determine how long it took the clay ball to fall to the ground, given that the height of the tower is 97.6 meters.

To solve the problem, it is necessary to remember that the path during uniformly accelerated motion is expressed by the formula: l=v 0 *t+g*t 2 /2. Since at the moment when Riccioli released the ball, the speed of the latter was equal to zero, then the term v 0 *t = 0. Then we come to the equation: 97.6 = 9.6*t 2 /2. Where do we get that t = 4.51 seconds ( negative root was deliberately discarded).
This topic may seem complicated at first due to the many not-so-simple formulas. Not only do the quadratic equations themselves have long notations, but the roots are also found through the discriminant. In total, three new formulas are obtained. Not very easy to remember. This is possible only after solving such equations frequently. Then all the formulas will be remembered by themselves.
General view of a quadratic equation
Here we propose their explicit recording, when the largest degree is written first, and then in descending order. There are often situations when the terms are inconsistent. Then it is better to rewrite the equation in descending order of the degree of the variable.
Let us introduce some notation. They are presented in the table below.
If we accept these notations, all quadratic equations are reduced to the following notation.

Moreover, the coefficient a ≠ 0. Let this formula be designated number one.
When an equation is given, it is not clear how many roots there will be in the answer. Because one of three options is always possible:
- the solution will have two roots;
- the answer will be one number;
- the equation will have no roots at all.
And until the decision is finalized, it is difficult to understand which option will appear in a particular case.
Types of recordings of quadratic equations
There may be different entries in tasks. They won't always look like general formula quadratic equation. Sometimes it will be missing some terms. What was written above is the complete equation. If you remove the second or third term in it, you get something else. These records are also called quadratic equations, only incomplete.
Moreover, only terms with coefficients “b” and “c” can disappear. The number "a" cannot be equal to zero under any circumstances. Because in this case the formula turns into a linear equation. The formulas for the incomplete form of equations will be as follows:
So, there are only two types; in addition to complete ones, there are also incomplete quadratic equations. Let the first formula be number two, and the second - three.
Discriminant and dependence of the number of roots on its value
You need to know this number in order to calculate the roots of the equation. It can always be calculated, no matter what the formula of the quadratic equation is. In order to calculate the discriminant, you need to use the equality written below, which will have number four.
After substituting the coefficient values into this formula, you can get numbers with different signs. If the answer is yes, then the answer to the equation will be two different roots. If the number is negative, there will be no roots of the quadratic equation. If it is equal to zero, there will be only one answer.
How to solve a complete quadratic equation?
In fact, consideration of this issue has already begun. Because first you need to find a discriminant. After it is determined that there are roots of the quadratic equation, and their number is known, you need to use formulas for the variables. If there are two roots, then you need to apply the following formula.

Since it contains a “±” sign, there will be two values. The expression under the square root sign is the discriminant. Therefore, the formula can be rewritten differently.
Formula number five. From the same record it is clear that if the discriminant is equal to zero, then both roots will take the same values.
If solving quadratic equations has not yet been worked out, then it is better to write down the values of all coefficients before applying the discriminant and variable formulas. Later this moment will not cause difficulties. But at the very beginning there is confusion.

How to solve an incomplete quadratic equation?
Everything is much simpler here. There is not even a need for additional formulas. And those that have already been written down for the discriminant and the unknown will not be needed.
First, let's look at incomplete equation number two. In this equality, it is necessary to take the unknown quantity out of brackets and solve the linear equation, which will remain in brackets. The answer will have two roots. The first one is necessarily equal to zero, because there is a multiplier consisting of the variable itself. The second one will be obtained by solving a linear equation.
Incomplete equation number three is solved by moving the number from the left side of the equality to the right. Then you need to divide by the coefficient facing the unknown. All that remains is to extract the square root and remember to write it down twice with opposite signs.

Below are some steps that will help you learn how to solve all kinds of equalities that turn into quadratic equations. They will help the student to avoid mistakes due to inattention. These shortcomings can cause poor grades when studying the extensive topic “Quadratic Equations (8th Grade).” Subsequently, these actions will not need to be performed constantly. Because a stable skill will appear.
- First you need to write the equation in standard form. That is, first the term with the largest degree of the variable, and then - without a degree, and last - just a number.
- If a minus appears before the coefficient “a”, it can complicate the work for a beginner studying quadratic equations. It's better to get rid of it. For this purpose, all equality must be multiplied by “-1”. This means that all terms will change sign to the opposite.
- It is recommended to get rid of fractions in the same way. Simply multiply the equation by the appropriate factor so that the denominators cancel out.

Examples
It is required to solve the following quadratic equations:
x 2 − 7x = 0;
15 − 2x − x 2 = 0;
x 2 + 8 + 3x = 0;
12x + x 2 + 36 = 0;
(x+1) 2 + x + 1 = (x+1)(x+2).
The first equation: x 2 − 7x = 0. It is incomplete, therefore it is solved as described for formula number two.
After taking it out of brackets, it turns out: x (x - 7) = 0.
The first root takes the value: x 1 = 0. The second will be found from linear equation: x - 7 = 0. It is easy to see that x 2 = 7.
Second equation: 5x 2 + 30 = 0. Again incomplete. Only it is solved as described for the third formula.
After moving 30 to the right side of the equation: 5x 2 = 30. Now you need to divide by 5. It turns out: x 2 = 6. The answers will be the numbers: x 1 = √6, x 2 = - √6.
The third equation: 15 − 2x − x 2 = 0. Here and further, solving quadratic equations will begin by rewriting them in standard form: − x 2 − 2x + 15 = 0. Now it’s time to use the second useful advice and multiply everything by minus one. It turns out x 2 + 2x - 15 = 0. Using the fourth formula, you need to calculate the discriminant: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. It is a positive number. From what is said above, it turns out that the equation has two roots. They need to be calculated using the fifth formula. It turns out that x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Then x 1 = 3, x 2 = - 5.
The fourth equation x 2 + 8 + 3x = 0 is transformed into this: x 2 + 3x + 8 = 0. Its discriminant is equal to this value: -23. Since this number is negative, the answer to this task will be the following entry: “There are no roots.”
The fifth equation 12x + x 2 + 36 = 0 should be rewritten as follows: x 2 + 12x + 36 = 0. After applying the formula for the discriminant, the number zero is obtained. This means that it will have one root, namely: x = -12/ (2 * 1) = -6.
The sixth equation (x+1) 2 + x + 1 = (x+1)(x+2) requires transformations, which consist in the fact that you need to bring similar terms, first opening the brackets. In place of the first there will be the following expression: x 2 + 2x + 1. After the equality, this entry will appear: x 2 + 3x + 2. After similar terms are counted, the equation will take the form: x 2 - x = 0. It has become incomplete . Something similar to this has already been discussed a little higher. The roots of this will be the numbers 0 and 1.
From this article you will learn:
What is it in appearance equations determine whether this equation will be incomplete quadratic equation? But as solve incomplete quadratic equations?
How to recognize an incomplete quadratic equation by sight
Left part of the equation ![]() There is quadratic trinomial, A right - number. Such equations are called full quadratic equations.
There is quadratic trinomial, A right - number. Such equations are called full quadratic equations.
U full quadratic equation All odds, And not equal. To solve them, there are special formulas, which we will get acquainted with later.
Most simple for solution are incomplete quadratic equations. These are quadratic equations in which some coefficients are zero.
Coefficient by definition cannot be zero, since otherwise the equation will not be quadratic. We talked about this. This means that it turns out that they can go to zero only odds or.
Depending on this there is three types of incomplete quadratic equations.
1)
![]() , Where ;
, Where ;
2)
, Where ;
3)
, Where .
So, if we see a quadratic equation, on the left side of which instead of three members present two dicks or one member, then the equation will be incomplete quadratic equation.
Definition of an incomplete quadratic equation
Incomplete quadratic equation This is called a quadratic equation ![]() , in which at least one of the coefficients or equal to zero.
, in which at least one of the coefficients or equal to zero.
This definition has a lot important phrase " at least one from the coefficients... equal to zero". It means that one or more coefficients can be equal zero.
Based on this, it is possible three options: or one coefficient is zero, or another coefficient is zero, or both coefficients are simultaneously equal to zero. This is how we get three types of incomplete quadratic equations.
Incomplete quadratic equations are the following equations:
1)
![]()
2)
![]()
3)
Solving the equation 
Let's outline solution plan this equation. Left part of the equation can be easily factorize, since on the left side of the equation the terms have common multiplier, it can be taken out of the bracket. Then on the left you get the product of two factors, and on the right - zero.
And then the rule “the product is equal to zero if and only if at least one of the factors is equal to zero, and the other makes sense” will work. Everything is very simple!
So, solution plan.
1)
We factor the left side into factors.
2) We use the rule “the product is equal to zero...”
I call equations of this type "a gift of fate". These are equations for which the right side is zero, A left part can be expanded by multipliers.
Solving the equation ![]() according to plan.
according to plan.
1)
Let's decompose left side of the equation by multipliers, for this we take out the common factor, we get the following equation ![]() .
.
2) In Eq. ![]() we see that left costs work, A zero on the right. Real a gift of fate! Here we, of course, will use the rule “the product is equal to zero if and only if at least one of the factors is equal to zero, and the other makes sense.” When translating this rule into the language of mathematics, we get two equations or .
we see that left costs work, A zero on the right. Real a gift of fate! Here we, of course, will use the rule “the product is equal to zero if and only if at least one of the factors is equal to zero, and the other makes sense.” When translating this rule into the language of mathematics, we get two equations or .
We see that the equation ![]() fell apart by two simpler equations, the first of which has already been solved ().
fell apart by two simpler equations, the first of which has already been solved ().
Let's solve the second one the equation . Let's move the unknown terms to the left and the known ones to the right. The unknown member is already on the left, we will leave him there. And let’s move the known term to the right from opposite sign. We get the equation.
We found it, but we need to find it. To get rid of the factor, you need to divide both sides of the equation by.
Quadratic equation - easy to solve! *Hereinafter referred to as “KU”. Friends, it would seem that there could be nothing simpler in mathematics than solving such an equation. But something told me that many people have problems with him. I decided to see how many on-demand impressions Yandex gives out per month. Here's what happened, look:

What does it mean? This means that about 70,000 people a month are looking for this information, what does this summer have to do with it, and what will happen among school year— there will be twice as many requests. This is not surprising, because those guys and girls who graduated from school a long time ago and are preparing for the Unified State Exam are looking for this information, and schoolchildren also strive to refresh their memory.
Despite the fact that there are a lot of sites that tell you how to solve this equation, I decided to also contribute and publish the material. Firstly, I want visitors to come to my site based on this request; secondly, in other articles, when the topic of “KU” comes up, I will provide a link to this article; thirdly, I’ll tell you a little more about his solution than is usually stated on other sites. Let's get started! The content of the article:
A quadratic equation is an equation of the form:

where coefficients a,band c are arbitrary numbers, with a≠0.
In the school course, the material is given in the following form– the equations are divided into three classes:
1. They have two roots.
2. *Have only one root.
3. They have no roots. It is worth especially noting here that they do not have real roots
How are roots calculated? Just!
We calculate the discriminant. Underneath this “terrible” word lies a very simple formula:
![]()
The root formulas are as follows:

*You need to know these formulas by heart.
You can immediately write down and solve:
Example:

1. If D > 0, then the equation has two roots.
2. If D = 0, then the equation has one root.
3. If D< 0, то уравнение не имеет действительных корней.
Let's look at the equation:

In this regard, when the discriminant is equal to zero, the school course says that one root is obtained, here it is equal to nine. Everything is correct, it is so, but...
This idea is somewhat incorrect. In fact, there are two roots. Yes, yes, don’t be surprised, you get two equal roots, and to be mathematically precise, then the answer should write two roots:
x 1 = 3 x 2 = 3
But this is so - a small digression. At school you can write it down and say that there is one root.
Now the next example:

As we know, the root of a negative number cannot be taken, so there is no solution in this case.
That's the whole decision process.
Quadratic function.
This shows what the solution looks like geometrically. This is extremely important to understand (in the future, in one of the articles we will analyze in detail the solution to the quadratic inequality).
This is a function of the form:

where x and y are variables
a, b, c – given numbers, with a ≠ 0
The graph is a parabola:
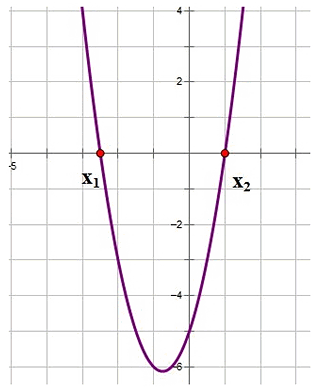
That is, it turns out that by solving a quadratic equation with “y” equal to zero, we find the points of intersection of the parabola with the x axis. There can be two of these points (the discriminant is positive), one (the discriminant is zero) and none (the discriminant is negative). Details about the quadratic function You can view article by Inna Feldman.
Let's look at examples:
Example 1: Solve 2x 2 +8 x–192=0
a=2 b=8 c= –192
D=b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Answer: x 1 = 8 x 2 = –12
*It was possible to immediately divide the left and right sides of the equation by 2, that is, simplify it. The calculations will be easier.
Example 2: Decide x 2–22 x+121 = 0
a=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

We found that x 1 = 11 and x 2 = 11
It is permissible to write x = 11 in the answer.
Answer: x = 11
Example 3: Decide x 2 –8x+72 = 0
a=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
The discriminant is negative, there is no solution in real numbers.
Answer: no solution
The discriminant is negative. There is a solution!
Here we will talk about solving the equation in the case when a negative discriminant is obtained. Do you know anything about complex numbers? I will not go into detail here about why and where they arose and what their specific role and necessity in mathematics is; this is a topic for a large separate article.
The concept of a complex number.
A little theory.
A complex number z is a number of the form
z = a + bi
where a and b are real numbers, i is the so-called imaginary unit.
a+bi – this is a SINGLE NUMBER, not an addition.
The imaginary unit is equal to the root of minus one:

Now consider the equation:

We get two conjugate roots.
Incomplete quadratic equation.
Let's consider special cases, this is when the coefficient “b” or “c” is equal to zero (or both are equal to zero). They can be solved easily without any discriminants.
Case 1. Coefficient b = 0.
The equation becomes:
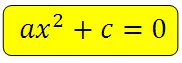
Let's transform:
Example:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Case 2. Coefficient c = 0.
The equation becomes:

Let's transform and factorize:

*The product is equal to zero when at least one of the factors is equal to zero.
Example:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 or x–5 =0
x 1 = 0 x 2 = 5
Case 3. Coefficients b = 0 and c = 0.

Here it is clear that the solution to the equation will always be x = 0.
Useful properties and patterns of coefficients.
There are properties that allow you to solve equations with large coefficients.
Ax 2 + bx+ c=0 equality holds
a + b+ c = 0, That

- if for the coefficients of the equation Ax 2 + bx+ c=0 equality holds
a+ c =b, That
![]()
These properties help solve a certain type of equation.
Example 1: 5001 x 2 –4995 x – 6=0
The sum of the odds is 5001+( – 4995)+(– 6) = 0, which means

Example 2: 2501 x 2 +2507 x+6=0
Equality holds a+ c =b, Means

Regularities of coefficients.
1. If in the equation ax 2 + bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 +1)∙x+ a= 0 = > x 1 = –a x 2 = –1/a.
Example. Consider the equation 6x 2 + 37x + 6 = 0.
x 1 = –6 x 2 = –1/6.
2. If in the equation ax 2 – bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 – (a 2 +1)∙x+ a= 0 = > x 1 = a x 2 = 1/a.
Example. Consider the equation 15x 2 –226x +15 = 0.
x 1 = 15 x 2 = 1/15.
3. If in Eq. ax 2 + bx – c = 0 coefficient “b” is equal to (a 2 – 1), and coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 –1)∙x – a= 0 = > x 1 = – a x 2 = 1/a.
Example. Consider the equation 17x 2 +288x – 17 = 0.
x 1 = – 17 x 2 = 1/17.
4. If in the equation ax 2 – bx – c = 0 the coefficient “b” is equal to (a 2 – 1), and the coefficient c is numerically equal to the coefficient “a”, then its roots are equal

ax 2 – (a 2 –1)∙x – a= 0 = > x 1 = a x 2 = – 1/a.
Example. Consider the equation 10x 2 – 99x –10 = 0.
x 1 = 10 x 2 = – 1/10
Vieta's theorem.
Vieta's theorem is named after the famous French mathematician Francois Vieta. Using Vieta's theorem, we can express the sum and product of the roots of an arbitrary KU in terms of its coefficients.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
In total, the number 14 gives only 5 and 9. These are roots. With a certain skill, using the presented theorem, you can solve many quadratic equations orally immediately.
Vieta's theorem, in addition. It is convenient in that after solving a quadratic equation in the usual way (through a discriminant), the resulting roots can be checked. I recommend doing this always.
TRANSPORTATION METHOD
With this method, the coefficient “a” is multiplied by the free term, as if “thrown” to it, which is why it is called "transfer" method. This method is used when the roots of the equation can be easily found using Vieta's theorem and, most importantly, when the discriminant is an exact square.
If A± b+c≠ 0, then the transfer technique is used, for example:
2X 2 – 11x+ 5 = 0 (1) => X 2 – 11x+ 10 = 0 (2)
Using Vieta's theorem in equation (2), it is easy to determine that x 1 = 10 x 2 = 1
The resulting roots of the equation must be divided by 2 (since the two were “thrown” from x 2), we get
x 1 = 5 x 2 = 0.5.
What is the rationale? Look what's happening.
The discriminants of equations (1) and (2) are equal:
If you look at the roots of the equations, you only get different denominators, and the result depends precisely on the coefficient of x 2:

The second (modified) one has roots that are 2 times larger.
Therefore, we divide the result by 2.
*If we reroll the three, we will divide the result by 3, etc.
Answer: x 1 = 5 x 2 = 0.5
Sq. ur-ie and Unified State Examination.
I’ll tell you briefly about its importance - YOU MUST BE ABLE TO DECIDE quickly and without thinking, you need to know the formulas of roots and discriminants by heart. Many of the problems included in the Unified State Examination tasks boil down to solving a quadratic equation (geometric ones included).
Something worth noting!
1. The form of writing an equation can be “implicit”. For example, the following entry is possible:
15+ 9x 2 - 45x = 0 or 15x+42+9x 2 - 45x=0 or 15 -5x+10x 2 = 0.
You need to bring it to a standard form (so as not to get confused when solving).
2. Remember that x is an unknown quantity and it can be denoted by any other letter - t, q, p, h and others.
In this article we will look at solving incomplete quadratic equations.
But first, let’s repeat what equations are called quadratic. An equation of the form ax 2 + bx + c = 0, where x is a variable, and the coefficients a, b and c are some numbers, and a ≠ 0, is called square. As we see, the coefficient for x 2 is not equal to zero, and therefore the coefficients for x or the free term can be equal to zero, in which case we get an incomplete quadratic equation.
There are three types of incomplete quadratic equations:
1) If b = 0, c ≠ 0, then ax 2 + c = 0;
2) If b ≠ 0, c = 0, then ax 2 + bx = 0;
3) If b = 0, c = 0, then ax 2 = 0.
- Let's figure out how to solve equations of the form ax 2 + c = 0.
To solve the equation, we move the free term c to the right side of the equation, we get
ax 2 = ‒s. Since a ≠ 0, we divide both sides of the equation by a, then x 2 = ‒c/a.
If ‒с/а > 0, then the equation has two roots
x = ±√(–c/a) .
If ‒c/a< 0, то это уравнение решений не имеет. Более наглядно решение данных уравнений представлено на схеме.
Let's try to understand with examples how to solve such equations.
Example 1. Solve the equation 2x 2 ‒ 32 = 0.
Answer: x 1 = - 4, x 2 = 4.
Example 2. Solve the equation 2x 2 + 8 = 0.
Answer: the equation has no solutions.
- Let's figure out how to solve it equations of the form ax 2 + bx = 0.
To solve the equation ax 2 + bx = 0, let's factorize it, that is, take x out of brackets, we get x(ax + b) = 0. The product is equal to zero if at least one of the factors is equal to zero. Then either x = 0, or ax + b = 0. Solving the equation ax + b = 0, we get ax = - b, whence x = - b/a. An equation of the form ax 2 + bx = 0 always has two roots x 1 = 0 and x 2 = ‒ b/a. See what the solution to equations of this type looks like in the diagram. 
Let's consolidate our knowledge with a specific example.
Example 3. Solve the equation 3x 2 ‒ 12x = 0.
x(3x ‒ 12) = 0
x= 0 or 3x – 12 = 0
Answer: x 1 = 0, x 2 = 4.
- Equations of the third type ax 2 = 0 are solved very simply.
If ax 2 = 0, then x 2 = 0. The equation has two equal roots x 1 = 0, x 2 = 0.
For clarity, let's look at the diagram. 
Let us make sure when solving Example 4 that equations of this type can be solved very simply.
Example 4. Solve the equation 7x 2 = 0.
Answer: x 1, 2 = 0.
It is not always immediately clear what type of incomplete quadratic equation we have to solve. Consider the following example.
Example 5. Solve the equation

Let's multiply both sides of the equation by a common denominator, that is, by 30

Let's cut it down
5(5x 2 + 9) – 6(4x 2 – 9) = 90.
Let's open the brackets
25x 2 + 45 – 24x 2 + 54 = 90.
Let's give similar
Let's move 99 from the left side of the equation to the right, changing the sign to the opposite
Answer: no roots.
We looked at how incomplete quadratic equations are solved. I hope that now you will not have any difficulties with such tasks. Be careful when determining the type of incomplete quadratic equation, then you will succeed.
If you have questions on this topic, sign up for my lessons, we will solve the problems that arise together.
website, when copying material in full or in part, a link to the source is required.

