Steps
Calculating sample variance
-
Record the sample values. In most cases, statisticians only have access to samples of specific populations. For example, as a rule, statisticians do not analyze the cost of maintaining the totality of all cars in Russia - they analyze a random sample of several thousand cars. Such a sample will help determine the average cost of a car, but, most likely, the resulting value will be far from the real one.
- For example, let's analyze the number of buns sold in a cafe over 6 days, taken in random order. The sample has next view: 17, 15, 23, 7, 9, 13. This is a sample, not a population, because we do not have data on buns sold for each day the cafe is open.
- If you are given a population rather than a sample of values, continue to the next section.
-
Write down a formula to calculate sample variance. Dispersion is a measure of the spread of values of a certain quantity. The closer the variance value is to zero, the closer the values are grouped together. When working with a sample of values, use the following formula to calculate variance:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2))– this is dispersion. Dispersion is measured in square units.
- x i (\displaystyle x_(i))– each value in the sample.
- x i (\displaystyle x_(i)) you need to subtract x̅, square it, and then add the results.
- x̅ – sample mean (sample mean).
- n – number of values in the sample.
-
Calculate the sample mean. It is denoted as x̅. The sample mean is calculated as a simple arithmetic mean: add up all the values in the sample, and then divide the result by the number of values in the sample.
- In our example, add the values in the sample: 15 + 17 + 23 + 7 + 9 + 13 = 84
Now divide the result by the number of values in the sample (in our example there are 6): 84 ÷ 6 = 14.
Sample mean x̅ = 14. - The sample mean is the central value around which the values in the sample are distributed. If the values in the sample cluster around the sample mean, then the variance is small; otherwise the variance is large.
- In our example, add the values in the sample: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
Subtract the sample mean from each value in the sample. Now calculate the difference x i (\displaystyle x_(i))- x̅, where x i (\displaystyle x_(i))– each value in the sample. Each result obtained indicates the degree of deviation of a particular value from the sample mean, that is, how far this value is from the sample mean.
- In our example:
x 1 (\displaystyle x_(1))- x = 17 - 14 = 3
x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - The correctness of the results obtained is easy to check, since their sum should be equal to zero. This is related to the determination of the average value, since negative values (distances from the average value to smaller values) are completely compensated positive values(distances from average to large values).
- In our example:
-
As noted above, the sum of the differences x i (\displaystyle x_(i))- x̅ must be equal to zero. It means that average variance is always equal to zero, which does not give any idea about the spread of values of a certain quantity. To solve this problem, square each difference x i (\displaystyle x_(i))- x̅. This will result in you only getting positive numbers, which will never add up to 0.
- In our example:
(x 1 (\displaystyle x_(1))- x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\displaystyle (x_(2))- x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - You found the square of the difference - x̅) 2 (\displaystyle ^(2)) for each value in the sample.
- In our example:
-
Calculate the sum of the squares of the differences. That is, find that part of the formula that is written like this: ∑[( x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))]. Here the sign Σ means the sum of squared differences for each value x i (\displaystyle x_(i)) in the sample. You have already found the squared differences (x i (\displaystyle (x_(i))- x̅) 2 (\displaystyle ^(2)) for each value x i (\displaystyle x_(i)) in the sample; now just add these squares.
- In our example: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
Divide the result by n - 1, where n is the number of values in the sample. Some time ago, to calculate sample variance, statisticians simply divided the result by n; in this case you will get the mean of the squared variance, which is ideal for describing the variance of a given sample. But remember that any sample is only a small part of the population of values. If you take another sample and perform the same calculations, you will get a different result. As it turns out, dividing by n - 1 (rather than just n) gives a more accurate estimate of the population variance, which is what you're interested in. Division by n – 1 has become common, so it is included in the formula for calculating sample variance.
- In our example, the sample includes 6 values, that is, n = 6.
Sample variance = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- In our example, the sample includes 6 values, that is, n = 6.
-
The difference between variance and standard deviation. Note that the formula contains an exponent, so the dispersion is measured in square units of the value being analyzed. Sometimes such a magnitude is quite difficult to operate; in such cases, use the standard deviation, which is equal to the square root of the variance. That is why the sample variance is denoted as s 2 (\displaystyle s^(2)), A standard deviation samples - how s (\displaystyle s).
- In our example, the standard deviation of the sample is: s = √33.2 = 5.76.
Calculating Population Variance
-
Analyze some set of values. The set includes all values of the quantity under consideration. For example, if you are studying the age of residents Leningrad region, then the population includes the ages of all residents of this area. When working with a population, it is recommended to create a table and enter the population values into it. Consider the following example:
- In a certain room there are 6 aquariums. Each aquarium contains the following number of fish:
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x 6 = 18 (\displaystyle x_(6)=18)
- In a certain room there are 6 aquariums. Each aquarium contains the following number of fish:
-
Write down a formula to calculate the population variance. Since the totality includes all values of a certain quantity, the formula below allows us to obtain exact value population variances. To distinguish population variance from sample variance (which is only an estimate), statisticians use various variables:
- σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/n
- σ 2 (\displaystyle ^(2))– population dispersion (read as “sigma squared”). Dispersion is measured in square units.
- x i (\displaystyle x_(i))– each value in its entirety.
- Σ – sum sign. That is, from each value x i (\displaystyle x_(i)) you need to subtract μ, square it, and then add the results.
- μ – population mean.
- n – number of values in the population.
-
Calculate the population mean. When working with a population, its mean is denoted as μ (mu). The population mean is calculated as a simple arithmetic mean: add up all the values in the population, and then divide the result by the number of values in the population.
- Keep in mind that averages are not always calculated as the arithmetic mean.
- In our example, the population mean: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
-
Subtract the population mean from each value in the population. The closer the difference is to zero, the closer specific meaning to the population mean. Find the difference between each value in the population and its mean, and you will get a first idea of the distribution of values.
- In our example:
x 1 (\displaystyle x_(1))- μ = 5 - 10.5 = -5.5
x 2 (\displaystyle x_(2))- μ = 5 - 10.5 = -5.5
x 3 (\displaystyle x_(3))- μ = 8 - 10.5 = -2.5
x 4 (\displaystyle x_(4))- μ = 12 - 10.5 = 1.5
x 5 (\displaystyle x_(5))- μ = 15 - 10.5 = 4.5
x 6 (\displaystyle x_(6))- μ = 18 - 10.5 = 7.5
- In our example:
-
Square each result obtained. The difference values will be both positive and negative; If these values are plotted on a number line, they will lie to the right and left of the population mean. This is not good for calculating variance because positive and negative numbers cancel each other out. So square each difference to get exclusively positive numbers.
- In our example:
(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) for each population value (from i = 1 to i = 6):
(-5,5)2 (\displaystyle ^(2)) = 30,25
(-5,5)2 (\displaystyle ^(2)), Where x n (\displaystyle x_(n))– the last value in the population. - To calculate the average value of the results obtained, you need to find their sum and divide it by n:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/n
- Now let's write down the above explanation using variables: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n and get a formula for calculating the population variance.
- In our example:
Where σ 2 j is the intragroup variance of the jth group.
For ungrouped data residual variance– measure of approximation accuracy, i.e. approximation of the regression line to the original data: 
where y(t) – forecast according to the trend equation; y t – initial dynamics series; n – number of points; p – number of regression equation coefficients (number of explanatory variables).
In this example it is called unbiased variance estimator.
Example No. 1. The distribution of workers of three enterprises of one association according to tariff categories is characterized by the following data:
| Worker's tariff category | Number of workers at the enterprise | ||
| enterprise 1 | enterprise 2 | enterprise 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Define:
1. variance for each enterprise (intra-group variances);
2. the average of the within-group variances;
3. intergroup dispersion;
4. total variance.
Solution.
Before starting to solve the problem, it is necessary to find out which feature is effective and which is factorial. In the example under consideration, the resultant attribute is “Tariff category”, and the factor attribute is “Number (name) of the enterprise”.
Then we have three groups (enterprises), for which it is necessary to calculate the group average and intragroup variances:
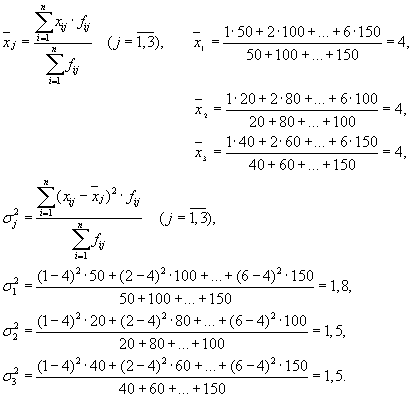
| Company | Group average, | Within-group variance, |
| 1 | 4 | 1,8 |
The average of the within-group variances ( residual variance) will be calculated using the formula:
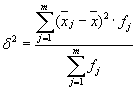
where you can calculate:

or:

Then:
The total variance will be equal to: s 2 = 1.6 + 0 = 1.6.
The total variance can also be calculated using one of the following two formulas:

When solving practical problems, one often has to deal with a feature that takes only two alternative values. In this case, we are not talking about the weight of a particular value of a feature, but about its share in the totality. If the proportion of population units possessing the characteristic being studied is denoted by “ R", and those who do not have - through " q", then the variance can be calculated using the formula:
s 2 = p×q
Example No. 2. Based on the data on the production of six working teams, determine the intergroup variance and evaluate the influence work shift on their labor productivity if the total variance is 12.2.
| Team worker no. | Worker output, pcs. | |
| in the first shift | in the second shift | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Solution. Initial data
| X | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | Total |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Total | 31 | 33 | 37 | 37 | 40 | 38 |
Then we have 6 groups for which it is necessary to calculate the group mean and intragroup variances.
1. Find the average values of each group.
2. Find the mean square of each group.
Let's summarize the calculation results in a table:
| Group number | Group average | Within-group variance |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Within-group variance characterizes the change (variation) of the studied (resultative) characteristic within a group under the influence of all factors on it, except for the factor underlying the grouping:
The average of the intragroup variances will be calculated using the formula:
4. Intergroup variance characterizes the change (variation) of the studied (resultative) characteristic under the influence of a factor (factorial characteristic) that forms the basis of the group.
We define intergroup variance as:
Where
Then
Total variance characterizes the change (variation) of the studied (resultative) characteristic under the influence of all factors (factorial characteristics) without exception. According to the conditions of the problem, it is equal to 12.2.
Empirical correlation relationship measures what part of the total variability of the resulting characteristic is caused by the factor being studied. This is the ratio of factor variance to total variance:
We define the empirical correlation relation:
Connections between characteristics can be weak and strong (close). Their criteria are assessed on the Chaddock scale:
0.1 0.3 0.5 0.7 0.9 In our example, the relationship between trait Y and factor X is weak
Determination coefficient.
Let's determine the coefficient of determination:
Thus, 0.67% of the variation is due to differences between traits, and 99.37% is due to other factors.
Conclusion: in this case, the output of workers does not depend on work on a specific shift, i.e. the influence of the work shift on their labor productivity is not significant and is due to other factors.
Example No. 3. Based on average wages and squared deviations from its value for two groups of workers, find the total variance by applying the rule of adding variances:
Solution:Average of within-group variances
We define intergroup variance as:
The total variance will be: 480 + 13824 = 14304
Probability theory is a special branch of mathematics that is studied only by students of higher educational institutions. Do you like calculations and formulas? Aren't you scared by the prospects of getting acquainted with the normal distribution, ensemble entropy, mathematical expectation and dispersion of a discrete random variable? Then this subject will be very interesting to you. Let's take a look at a few of the most important basic concepts this branch of science.
Let's remember the basics
Even if you remember the simplest concepts of probability theory, do not neglect the first paragraphs of the article. The point is that without a clear understanding of the basics, you will not be able to work with the formulas discussed below.
So, some random event occurs, some experiment. As a result of the actions we take, we can get several outcomes - some of them occur more often, others less often. The probability of an event is the ratio of the number of actually obtained outcomes of one type to total number possible. Only knowing the classic definition of this concept can you begin to study mathematical expectation and variances of continuous random variables.
Average
Back in school, during math lessons, you started working with the arithmetic mean. This concept is widely used in probability theory, and therefore cannot be ignored. The main thing for us is this moment is that we will encounter it in the formulas for the mathematical expectation and dispersion of a random variable.

We have a sequence of numbers and want to find the arithmetic mean. All that is required of us is to sum up everything available and divide by the number of elements in the sequence. Let us have numbers from 1 to 9. The sum of the elements will be equal to 45, and we will divide this value by 9. Answer: - 5.
Dispersion
In scientific terms, dispersion is the average square of deviations of the obtained values of a characteristic from the arithmetic mean. It is denoted by one capital Latin letter D. What is needed to calculate it? For each element of the sequence, we calculate the difference between the existing number and the arithmetic mean and square it. There will be exactly as many values as there can be outcomes for the event we are considering. Next, we sum up everything received and divide by the number of elements in the sequence. If we have five possible outcomes, then divide by five.

Dispersion also has properties that need to be remembered in order to be used when solving problems. For example, when increasing a random variable by X times, the variance increases by X squared times (i.e. X*X). She never happens less than zero and does not depend on shifting values by an equal value up or down. Additionally, for independent trials, the variance of the sum is equal to the sum of the variances.
Now we definitely need to consider examples of the variance of a discrete random variable and the mathematical expectation.
Let's say we ran 21 experiments and got 7 different outcomes. We observed each of them 1, 2, 2, 3, 4, 4 and 5 times, respectively. What will the variance be equal to?
First, let's calculate the arithmetic mean: the sum of the elements, of course, is 21. Divide it by 7, getting 3. Now subtract 3 from each number in the original sequence, square each value, and add the results together. The result is 12. Now all we have to do is divide the number by the number of elements, and, it would seem, that’s all. But there's a catch! Let's discuss it.
Dependence on the number of experiments
It turns out that when calculating variance, the denominator can contain one of two numbers: either N or N-1. Here N is the number of experiments performed or the number of elements in the sequence (which is essentially the same thing). What does this depend on?

If the number of tests is measured in hundreds, then we must put N in the denominator. If in units, then N-1. Scientists decided to draw the border quite symbolically: today it passes through the number 30. If we conducted less than 30 experiments, then we will divide the amount by N-1, and if more, then by N.
Task
Let's return to our example of solving the problem of variance and mathematical expectation. We got an intermediate number 12, which needed to be divided by N or N-1. Since we conducted 21 experiments, which is less than 30, we will choose the second option. So the answer is: the variance is 12 / 2 = 2.
Expected value
Let's move on to the second concept, which we must consider in this article. The mathematical expectation is the result of adding all possible outcomes multiplied by the corresponding probabilities. It is important to understand that the obtained value, as well as the result of calculating the variance, is obtained only once for the entire problem, no matter how many outcomes are considered in it.

The formula for mathematical expectation is quite simple: we take the outcome, multiply it by its probability, add the same for the second, third result, etc. Everything related to this concept is not difficult to calculate. For example, the sum of the expected values is equal to the expected value of the sum. The same is true for the work. Not every quantity in probability theory allows you to perform such simple operations. Let's take the problem and calculate the meaning of two concepts we have studied at once. Besides, we were distracted by theory - it's time to practice.
One more example
We ran 50 trials and got 10 types of outcomes - numbers from 0 to 9 - appearing in different percentages. These are, respectively: 2%, 10%, 4%, 14%, 2%,18%, 6%, 16%, 10%, 18%. Recall that to obtain probabilities, you need to divide the percentage values by 100. Thus, we get 0.02; 0.1, etc. Let us present an example of solving the problem for the variance of a random variable and the mathematical expectation.
We calculate the arithmetic mean using the formula that we remember from junior school: 50/10 = 5.
Now let’s convert the probabilities into the number of outcomes “in pieces” to make it easier to count. We get 1, 5, 2, 7, 1, 9, 3, 8, 5 and 9. From each value obtained, we subtract the arithmetic mean, after which we square each of the results obtained. See how to do this using the first element as an example: 1 - 5 = (-4). Next: (-4) * (-4) = 16. For other values, do these operations yourself. If you did everything correctly, then after adding them all up you will get 90.

Let's continue calculating the variance and expected value by dividing 90 by N. Why do we choose N rather than N-1? Correct, because the number of experiments performed exceeds 30. So: 90/10 = 9. We got the variance. If you get a different number, don't despair. Most likely, you made a simple mistake in the calculations. Double-check what you wrote, and everything will probably fall into place.
Finally, remember the formula for mathematical expectation. We will not give all the calculations, we will only write an answer that you can check with after completing all the required procedures. The expected value will be 5.48. Let us only recall how to carry out operations, using the first elements as an example: 0*0.02 + 1*0.1... and so on. As you can see, we simply multiply the outcome value by its probability.
Deviation
Another concept closely related to dispersion and mathematical expectation is standard deviation. It is denoted either by the Latin letters sd, or by the Greek lowercase “sigma”. This concept shows how much on average the values deviate from the central feature. To find its value, you need to calculate Square root from dispersion.

If you plot a normal distribution graph and want to see the squared deviation directly on it, this can be done in several stages. Take half of the image to the left or right of the mode (central value), draw a perpendicular to the horizontal axis so that the areas of the resulting figures are equal. The size of the segment between the middle of the distribution and the resulting projection onto the horizontal axis will represent the standard deviation.
Software
As can be seen from the descriptions of the formulas and the examples presented, calculating variance and mathematical expectation is not the simplest procedure from an arithmetic point of view. In order not to waste time, it makes sense to use the program used in higher education educational institutions- it's called "R". It has functions that allow you to calculate values for many concepts from statistics and probability theory.
For example, you specify a vector of values. This is done as follows: vector<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.
Finally
Dispersion and mathematical expectation are without which it is difficult to calculate anything in the future. In the main course of lectures at universities, they are discussed already in the first months of studying the subject. It is precisely because of the lack of understanding of these simple concepts and the inability to calculate them that many students immediately begin to fall behind in the program and later receive bad grades at the end of the session, which deprives them of scholarships.
Practice for at least one week, half an hour a day, solving tasks similar to those presented in this article. Then, on any test in probability theory, you will be able to cope with the examples without extraneous tips and cheat sheets.
Dispersion in statistics is defined as the standard deviation of individual values of a characteristic squared from the arithmetic mean. A common method for calculating the squared deviations of options from the average and then averaging them.
![]()
In economic statistical analysis, it is customary to evaluate the variation of a characteristic most often using the standard deviation; it is the square root of the variance.
 (3)
(3)
Characterizes the absolute fluctuation of the values of a varying characteristic and is expressed in the same units of measurement as the options. In statistics, there is often a need to compare the variation of different characteristics. For such comparisons, a relative measure of variation, the coefficient of variation, is used.
Dispersion properties:
1) if you subtract any number from all options, then the variance will not change;
2) if all values of the option are divided by any number b, then the variance will decrease by b^2 times, i.e.
3) if you calculate the average square of deviations from any number with an unequal arithmetic mean, then it will be greater than the variance. At the same time, by a well-defined value per square of the difference between the average value c.
![]()
Dispersion can be defined as the difference between the mean squared and the mean squared.
17. Group and intergroup variations. Variance addition rule
If a statistical population is divided into groups or parts according to the characteristic being studied, then the following types of dispersion can be calculated for such a population: group (private), group average (private), and intergroup.
Total variance– reflects the variation of a characteristic due to all the conditions and causes operating in a given statistical population. ![]()
Group variance- equal to the mean square of deviations of individual values of a characteristic within a group from the arithmetic mean of this group, called the group mean. However, the group average does not coincide with the overall average for the entire population.
![]()
Group variance reflects the variation of a trait only due to conditions and causes operating within the group.
Average of group variances- is defined as the weighted arithmetic mean of the group variances, with the weights being the group volumes.
Intergroup variance- equal to the mean square of deviations of group averages from the overall average.
Intergroup dispersion characterizes the variation of the resulting characteristic due to the grouping characteristic.
There is a certain relationship between the types of dispersions considered: the total dispersion is equal to the sum of the average group and intergroup dispersion.
This relationship is called the variance addition rule.
18. Dynamic series and its components. Types of time series.
Row in statistics- this is digital data that shows the change of a phenomenon in time or space and makes it possible to make a statistical comparison of phenomena both in the process of their development in time and in various forms and types of processes. Thanks to this, it is possible to detect the mutual dependence of phenomena.
In statistics, the process of development of the movement of social phenomena over time is usually called dynamics. To display dynamics, dynamics series (chronological, time) are constructed, which are series of time-varying values of a statistical indicator (for example, the number of convicted people over 10 years), arranged in chronological order. Their constituent elements are the digital values of a given indicator and the periods or points in time to which they relate.
The most important characteristic of dynamics series- their size (volume, magnitude) of a particular phenomenon achieved in a certain period or at a certain moment. Accordingly, the magnitude of the terms of the dynamics series is its level. Distinguish initial, middle and final levels of the dynamic series. First level shows the value of the first, the final - the value of the last term of the series. Average level represents the average chronological variation range and is calculated depending on whether the dynamic series is interval or momentary.
Another important characteristic of the dynamic series- the time elapsed from the initial to the final observation, or the number of such observations.
There are different types of time series; they can be classified according to the following criteria.
1) Depending on the method of expressing the levels, the dynamics series are divided into series of absolute and derivative indicators (relative and average values).
2) Depending on how the levels of the series express the state of the phenomenon at certain points in time (at the beginning of the month, quarter, year, etc.) or its value over certain time intervals (for example, per day, month, year, etc.) etc.), distinguish between moment and interval dynamics series, respectively. Moment series are used relatively rarely in the analytical work of law enforcement agencies.
In statistical theory, dynamics are distinguished according to a number of other classification criteria: depending on the distance between levels - with equal levels and unequal levels in time; depending on the presence of the main tendency of the process being studied - stationary and non-stationary. When analyzing time series, they proceed from the following; the levels of the series are presented in the form of components:
Y t = TP + E (t)
where TP is a deterministic component that determines the general tendency of change over time or trend.
E (t) is a random component that causes fluctuations in levels.
Expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of scattering. In many practical problems, a complete, exhaustive characteristic of a random variable - the distribution law - either cannot be obtained at all, or is not needed at all. In these cases, one is limited to an approximate description of a random variable using numerical characteristics.
The expected value is often called simply the average value of a random variable. Dispersion of a random variable is a characteristic of dispersion, the spread of a random variable around its mathematical expectation.
Expectation of a discrete random variable
Let us approach the concept of mathematical expectation, first based on the mechanical interpretation of the distribution of a discrete random variable. Let the unit mass be distributed between the points of the x-axis x1 , x 2 , ..., x n, and each material point has a corresponding mass of p1 , p 2 , ..., p n. It is required to select one point on the abscissa axis, characterizing the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, to which the abscissa of each point xi enters with a “weight” equal to the corresponding probability. The average value of the random variable obtained in this way X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:
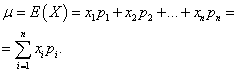
Example 1. A win-win lottery has been organized. There are 1000 winnings, of which 400 are 10 rubles. 300 - 20 rubles each. 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for someone who buys one ticket?
Solution. We will find the average winnings if we divide the total amount of winnings, which is 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, by 1000 (total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average winnings can be presented in the following form:
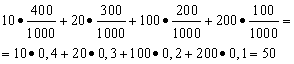
On the other hand, in these conditions, the winning size is a random variable, which can take values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average win is equal to the sum of the products of the size of the wins and the probability of receiving them.
Example 2. The publisher decided to publish a new book. He plans to sell the book for 280 rubles, of which he himself will receive 200, 50 - the bookstore and 30 - the author. The table provides information about the costs of publishing a book and the probability of selling a certain number of copies of the book.
Find the publisher's expected profit.
Solution. The random variable “profit” is equal to the difference between the income from sales and the cost of expenses. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publication is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher’s profit:
![]() .
.
Example 3. Probability of hitting with one shot p= 0.2. Determine the consumption of projectiles that provide a mathematical expectation of the number of hits equal to 5.
Solution. From the same mathematical expectation formula that we have used so far, we express x- shell consumption:
![]() .
.
Example 4. Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of a hit with each shot p = 0,4 .
Hint: find the probability of random variable values by Bernoulli's formula .
Properties of mathematical expectation
Let's consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the mathematical expectation sign:
![]()
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of a product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of a random variable X decrease (increase) by the same number WITH, then its mathematical expectation will decrease (increase) by the same number:
![]()
When you can’t limit yourself only to mathematical expectation
In most cases, only the mathematical expectation cannot sufficiently characterize a random variable.
Let the random variables X And Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:
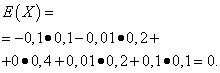
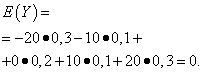
However, their distribution patterns are different. Random value X can only take values that differ little from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average wage does not make it possible to judge the share of high- and low-paid workers. In other words, one cannot judge from the mathematical expectation what deviations from it, at least on average, are possible. To do this, you need to find the variance of the random variable.
Variance of a discrete random variable
Variance discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:
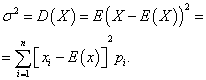
The standard deviation of a random variable X the arithmetic value of the square root of its variance is called:
![]() .
.
Example 5. Calculate variances and standard deviations of random variables X And Y, the distribution laws of which are given in the tables above.
Solution. Mathematical expectations of random variables X And Y, as found above, are equal to zero. According to the dispersion formula at E(X)=E(y)=0 we get:

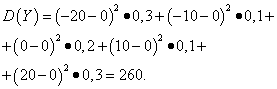
Then the standard deviations of random variables X And Y make up
![]() .
.
Thus, with the same mathematical expectations, the variance of the random variable X very small, but a random variable Y- significant. This is a consequence of differences in their distribution.
Example 6. The investor has 4 alternative investment projects. The table summarizes the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find the mathematical expectation, variance and standard deviation for each alternative.
Solution. Let us show how these values are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectations. This means that in the long run everyone has the same income. Standard deviation can be interpreted as a measure of risk - the higher it is, the greater the risk of the investment. An investor who does not want much risk will choose project 1 since it has the smallest standard deviation (0). If the investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation - project 4.
Dispersion properties
Let us present the properties of dispersion.
Property 1. The variance of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
![]() .
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
![]() ,
,
Where ![]() .
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7. It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Solution. Let us denote by p the probability with which a random variable takes a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let us derive the equation for the mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
Law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of dispersion:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then look at the solution
Example 8. Discrete random variable X takes only two values. It accepts the greater of the values 3 with probability 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9. There are 6 white and 4 black balls in the urn. 3 balls are drawn from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Solution. Random value X can take values 0, 1, 2, 3. The corresponding probabilities can be calculated from probability multiplication rule. Law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Expectation and variance of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). Unlike a discrete random variable, whose function argument xi changes abruptly; for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its average value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If the density function of a continuous random variable is given, then it directly enters into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .

