Το άρθρο παρέχει μια λεπτομερή εξήγηση των ορισμών, τη γεωμετρική σημασία της παραγώγου με γραφικές σημειώσεις. Η εξίσωση μιας εφαπτομένης ευθείας θα εξεταστεί με παραδείγματα, θα βρεθούν οι εξισώσεις μιας εφαπτομένης σε καμπύλες 2ης τάξης.
Yandex.RTB R-A-339285-1 Ορισμός 1
Η γωνία κλίσης της ευθείας y = k x + b ονομάζεται γωνία α, η οποία μετράται από τη θετική φορά του άξονα x στην ευθεία y = k x + b στη θετική κατεύθυνση.
Στο σχήμα, η κατεύθυνση x υποδεικνύεται με ένα πράσινο βέλος και ένα πράσινο τόξο και η γωνία κλίσης με ένα κόκκινο τόξο. Η μπλε γραμμή αναφέρεται στην ευθεία γραμμή.
Ορισμός 2
Η κλίση της ευθείας y = k x + b ονομάζεται αριθμητικός συντελεστής k.
Ο γωνιακός συντελεστής είναι ίσος με την εφαπτομένη της ευθείας, με άλλα λόγια k = t g α.
- Η γωνία κλίσης μιας ευθείας είναι ίση με 0 μόνο αν είναι παράλληλη περίπου x και η κλίση είναι ίση με μηδέν, επειδή η εφαπτομένη του μηδέν είναι ίση με 0. Αυτό σημαίνει ότι η μορφή της εξίσωσης θα είναι y = b.
- Αν η γωνία κλίσης της ευθείας y = k x + b είναι οξεία, τότε ικανοποιούνται οι συνθήκες 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, και υπάρχει μια αύξηση στο γράφημα.
- Αν α = π 2, τότε η θέση της ευθείας είναι κάθετη στο x. Η ισότητα καθορίζεται από το x = c με την τιμή c να είναι πραγματικός αριθμός.
- Αν η γωνία κλίσης της ευθείας y = k x + b είναι αμβλεία, τότε αντιστοιχεί στις συνθήκες π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Τομή είναι μια ευθεία που διέρχεται από 2 σημεία της συνάρτησης f (x). Με άλλα λόγια, μια διατομή είναι μια ευθεία γραμμή που τραβιέται μέσα από οποιαδήποτε δύο σημεία του γραφήματος δεδομένη λειτουργία.

Το σχήμα δείχνει ότι το A B είναι μια τομή και η f (x) είναι μια μαύρη καμπύλη, το α είναι ένα κόκκινο τόξο, που δείχνει τη γωνία κλίσης της τομής.
Όταν ο γωνιακός συντελεστής μιας ευθείας γραμμής είναι ίσος με την εφαπτομένη της γωνίας κλίσης, είναι σαφές ότι η εφαπτομένη ενός ορθογωνίου τριγώνου A B C μπορεί να βρεθεί από το λόγο της απέναντι πλευράς προς τη διπλανή.
Ορισμός 4
Λαμβάνουμε έναν τύπο για την εύρεση μιας τομής της φόρμας:
k = t g α = B C A C = f (x B) - f x A x B - x A, όπου τα τετμημένα των σημείων A και B είναι οι τιμές x A, x B και f (x A), f (x Β) είναι οι συναρτήσεις τιμών σε αυτά τα σημεία.
Προφανώς, ο γωνιακός συντελεστής της τομής προσδιορίζεται χρησιμοποιώντας την ισότητα k = f (x B) - f (x A) x B - x A ή k = f (x A) - f (x B) x A - x B , και η εξίσωση πρέπει να γραφεί ως y = f (x B) - f (x A) x B - x A x - x A + f (x A) ή
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .
Η τομή διαιρεί το γράφημα οπτικά σε 3 μέρη: στα αριστερά του σημείου Α, από το Α στο Β, στα δεξιά του Β. Το παρακάτω σχήμα δείχνει ότι υπάρχουν τρεις διατομές που θεωρούνται συμπίπτουσες, δηλαδή ορίζονται χρησιμοποιώντας ένα παρόμοια εξίσωση.

Εξ ορισμού, είναι σαφές ότι η ευθεία γραμμή και η τομή της σε αυτήν την περίπτωση συμπίπτουν.
Μια τομή μπορεί να τέμνει το γράφημα μιας δεδομένης συνάρτησης πολλές φορές. Αν υπάρχει εξίσωση της μορφής y = 0 για μια τομή, τότε ο αριθμός των σημείων τομής με το ημιτονοειδές είναι άπειρος.
Ορισμός 5
Εφαπτομένη στη γραφική παράσταση της συνάρτησης f (x) στο σημείο x 0 ; f (x 0) είναι μια ευθεία που διέρχεται από ένα δεδομένο σημείο x 0. f (x 0), με την παρουσία ενός τμήματος που έχει πολλές τιμές x κοντά στο x 0.
Παράδειγμα 1
Ας ρίξουμε μια πιο προσεκτική ματιά στο παρακάτω παράδειγμα. Τότε είναι σαφές ότι η ευθεία που ορίζεται από τη συνάρτηση y = x + 1 θεωρείται εφαπτομένη της y = 2 x στο σημείο με συντεταγμένες (1; 2). Για λόγους σαφήνειας, είναι απαραίτητο να ληφθούν υπόψη γραφήματα με τιμές κοντά στο (1; 2). Η συνάρτηση y = 2 x εμφανίζεται με μαύρο χρώμα, η μπλε γραμμή είναι η εφαπτομένη και η κόκκινη κουκκίδα είναι το σημείο τομής.

Προφανώς, το y = 2 x συγχωνεύεται με την ευθεία y = x + 1.
Για να προσδιορίσουμε την εφαπτομένη, θα πρέπει να εξετάσουμε τη συμπεριφορά της εφαπτομένης Α Β καθώς το σημείο Β πλησιάζει άπειρα το σημείο Α. Για λόγους σαφήνειας, παρουσιάζουμε ένα σχέδιο.

Η τομή A B, που υποδεικνύεται από την μπλε γραμμή, τείνει στη θέση της ίδιας της εφαπτομένης και η γωνία κλίσης της τομής α θα αρχίσει να τείνει προς τη γωνία κλίσης της ίδιας της εφαπτομένης α x.
Ορισμός 6
Η εφαπτομένη στη γραφική παράσταση της συνάρτησης y = f (x) στο σημείο Α θεωρείται ως η οριακή θέση της τομής Α Β καθώς το Β τείνει στο Α, δηλαδή Β → Α.
Τώρα ας προχωρήσουμε στην εξέταση της γεωμετρικής σημασίας της παραγώγου μιας συνάρτησης σε ένα σημείο.
Ας προχωρήσουμε στην εξέταση της διατομής A B για τη συνάρτηση f (x), όπου τα A και B με συντεταγμένες x 0, f (x 0) και x 0 + ∆ x, f (x 0 + ∆ x), και το ∆ x είναι συμβολίζεται ως η προσαύξηση του επιχειρήματος . Τώρα η συνάρτηση θα πάρει τη μορφή ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Για λόγους σαφήνειας, ας δώσουμε ένα παράδειγμα σχεδίου.

Ας εξετάσουμε το αποτέλεσμα ορθογώνιο τρίγωνο A B C. Χρησιμοποιούμε τον ορισμό της εφαπτομένης για να λύσουμε, δηλαδή παίρνουμε τη σχέση ∆ y ∆ x = t g α . Από τον ορισμό της εφαπτομένης προκύπτει ότι lim ∆ x → 0 ∆ y ∆ x = t g α x . Σύμφωνα με τον κανόνα της παραγώγου σε ένα σημείο, έχουμε ότι η παράγωγος f (x) στο σημείο x 0 ονομάζεται όριο του λόγου της αύξησης της συνάρτησης προς την αύξηση του ορίσματος, όπου Δ x → 0 , τότε το συμβολίζουμε ως f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Έπεται ότι f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, όπου το k x συµβολίζεται ως η κλίση της εφαπτοµένης.
Δηλαδή, παίρνουμε ότι η f ’ (x) μπορεί να υπάρχει στο σημείο x 0 και σαν την εφαπτομένη δεδομένο χρονοδιάγραμμασυνάρτηση στο σημείο της εφαπτομένης ίσης με x 0, f 0 (x 0), όπου η τιμή της κλίσης της εφαπτομένης στο σημείο είναι ίση με την παράγωγο στο σημείο x 0. Τότε παίρνουμε ότι k x = f " (x 0) .
Η γεωμετρική σημασία της παραγώγου μιας συνάρτησης σε ένα σημείο είναι ότι δίνει την έννοια της ύπαρξης εφαπτομένης στη γραφική παράσταση στο ίδιο σημείο.
Για να γράψουμε την εξίσωση οποιασδήποτε ευθείας σε ένα επίπεδο, είναι απαραίτητο να έχουμε έναν γωνιακό συντελεστή με το σημείο από το οποίο διέρχεται. Ο συμβολισμός του λαμβάνεται ως x 0 στη διασταύρωση.
Η εφαπτομένη εξίσωση στη γραφική παράσταση της συνάρτησης y = f (x) στο σημείο x 0, f 0 (x 0) παίρνει τη μορφή y = f "(x 0) x - x 0 + f (x 0).
Αυτό σημαίνει ότι η τελική τιμή της παραγώγου f "(x 0) μπορεί να καθορίσει τη θέση της εφαπτομένης, δηλαδή κατακόρυφα, με την προϋπόθεση lim x → x 0 + 0 f "(x) = ∞ και lim x → x 0 - 0 f "(x) = ∞ ή καθόλου υπό την προϋπόθεση lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .
Η θέση της εφαπτομένης εξαρτάται από την τιμή του γωνιακού της συντελεστή k x = f "(x 0). Όταν είναι παράλληλη με τον άξονα o x, λαμβάνουμε ότι k k = 0, όταν είναι παράλληλη με o y - k x = ∞, και τη μορφή του Η εφαπτομένη εξίσωση x = x 0 αυξάνεται με k x > 0, μειώνεται ως k x< 0 .
Παράδειγμα 2
Να συντάξετε μια εξίσωση για την εφαπτομένη στη γραφική παράσταση της συνάρτησης y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 στο σημείο με συντεταγμένες (1; 3) και προσδιορίστε τη γωνία κλίσης.
Λύση
Με προϋπόθεση, έχουμε ότι η συνάρτηση ορίζεται για όλους τους πραγματικούς αριθμούς. Βρίσκουμε ότι το σημείο με τις συντεταγμένες που καθορίζονται από τη συνθήκη, (1; 3) είναι ένα σημείο εφαπτομένης, τότε x 0 = - 1, f (x 0) = - 3.
Είναι απαραίτητο να βρείτε την παράγωγο στο σημείο με τιμή - 1. Το καταλαβαίνουμε
y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Η τιμή του f' (x) στο σημείο της εφαπτομένης είναι η κλίση της εφαπτομένης, η οποία είναι ίση με την εφαπτομένη της κλίσης.
Τότε k x = t g α x = y " (x 0) = 3 3
Έπεται ότι α x = a r c t g 3 3 = π 6
Απάντηση:η εφαπτομενική εξίσωση παίρνει τη μορφή
y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3
Για λόγους σαφήνειας, δίνουμε ένα παράδειγμα σε μια γραφική απεικόνιση.
Το μαύρο χρώμα χρησιμοποιείται για το γράφημα της αρχικής συνάρτησης, Μπλε χρώμα– εικόνα εφαπτομένης, κόκκινη κουκκίδα – σημείο εφαπτομένης. Το σχήμα στα δεξιά δείχνει μια μεγεθυμένη προβολή.

Παράδειγμα 3
Να προσδιορίσετε την ύπαρξη εφαπτομένης στη γραφική παράσταση μιας δεδομένης συνάρτησης
y = 3 · x - 1 5 + 1 στο σημείο με συντεταγμένες (1 ; 1) . Γράψτε μια εξίσωση και προσδιορίστε τη γωνία κλίσης.
Λύση
Υπό την προϋπόθεση, έχουμε ότι το πεδίο ορισμού μιας δεδομένης συνάρτησης θεωρείται ότι είναι το σύνολο όλων των πραγματικών αριθμών.
Ας προχωρήσουμε στην εύρεση της παραγώγου
y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Αν x 0 = 1, τότε η f' (x) δεν έχει οριστεί, αλλά τα όρια γράφονται ως lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ και lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , που σημαίνει ύπαρξη κάθετης εφαπτομένης στο σημείο (1; 1).
Απάντηση:η εξίσωση θα πάρει τη μορφή x = 1, όπου η γωνία κλίσης θα είναι ίση με π 2.
Για λόγους σαφήνειας, ας το απεικονίσουμε γραφικά.

Παράδειγμα 4
Βρείτε τα σημεία στη γραφική παράσταση της συνάρτησης y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, όπου
- Δεν υπάρχει εφαπτομένη.
- Η εφαπτομένη είναι παράλληλη στο x.
- Η εφαπτομένη είναι παράλληλη στην ευθεία y = 8 5 x + 4.
Λύση
Είναι απαραίτητο να δοθεί προσοχή στο εύρος του ορισμού. Με προϋπόθεση, έχουμε ότι η συνάρτηση ορίζεται στο σύνολο όλων των πραγματικών αριθμών. Επεκτείνουμε την ενότητα και λύνουμε το σύστημα με διαστήματα x ∈ - ∞ ; 2 και [-2; + ∞) . Το καταλαβαίνουμε
y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)
Είναι απαραίτητο να διαφοροποιηθεί η συνάρτηση. Το έχουμε αυτό
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 ", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)
Όταν x = − 2, τότε η παράγωγος δεν υπάρχει γιατί τα μονόπλευρα όρια δεν είναι ίσα σε αυτό το σημείο:
lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Υπολογίζουμε την τιμή της συνάρτησης στο σημείο x = - 2, όπου και προκύπτει
- y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, δηλαδή η εφαπτομένη στο σημείο ( - 2; - 2) δεν θα υπάρχει.
- Η εφαπτομένη είναι παράλληλη στο x όταν η κλίση είναι μηδέν. Τότε k x = t g α x = f "(x 0). Δηλαδή, είναι απαραίτητο να βρεθούν οι τιμές αυτού του x όταν η παράγωγος της συνάρτησης τη μηδενίσει. Δηλαδή, οι τιμές του f ' (x) θα είναι τα σημεία εφαπτομένης, όπου η εφαπτομένη είναι παράλληλη στο x .
Όταν x ∈ - ∞ ; - 2, μετά - 1 5 (x 2 + 12 x + 35) = 0, και για x ∈ (- 2; + ∞) παίρνουμε 1 5 (x 2 - 4 x + 3) = 0.
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Υπολογίστε τις αντίστοιχες τιμές συνάρτησης
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Ως εκ τούτου - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 θεωρούνται τα απαιτούμενα σημεία του γραφήματος συνάρτησης.
Ας δούμε μια γραφική αναπαράσταση της λύσης.

Η μαύρη γραμμή είναι το γράφημα της συνάρτησης, οι κόκκινες τελείες είναι τα σημεία εφαπτομένης.
- Όταν οι ευθείες είναι παράλληλες, οι γωνιακοί συντελεστές είναι ίσοι. Στη συνέχεια, είναι απαραίτητο να αναζητήσετε σημεία στο γράφημα συνάρτησης όπου η κλίση θα είναι ίση με την τιμή 8 5. Για να το κάνετε αυτό, πρέπει να λύσετε μια εξίσωση της μορφής y "(x) = 8 5. Τότε, αν x ∈ - ∞; - 2, λαμβάνουμε ότι - 1 5 (x 2 + 12 x + 35) = 8 5, και αν x ∈ ( - 2 ; + ∞), τότε 1 5 (x 2 - 4 x + 3) = 8 5.
Η πρώτη εξίσωση δεν έχει ρίζες, αφού η διάκριση λιγότερο από το μηδέν. Ας το γράψουμε αυτό
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Μια άλλη εξίσωση έχει δύο πραγματικές ρίζες, λοιπόν
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Ας προχωρήσουμε στην εύρεση των τιμών της συνάρτησης. Το καταλαβαίνουμε
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Πόντοι με τιμές - 1; 4 15, 5; 8 3 είναι τα σημεία στα οποία οι εφαπτομένες είναι παράλληλες στην ευθεία y = 8 5 x + 4.
Απάντηση:μαύρη γραμμή – γράφημα της συνάρτησης, κόκκινη γραμμή – γράφημα του y = 8 5 x + 4, μπλε γραμμή – εφαπτομένες στα σημεία - 1; 4 15, 5; 8 3.

Μπορεί να υπάρχει άπειρος αριθμός εφαπτομένων για δεδομένες συναρτήσεις.
Παράδειγμα 5
Να γράψετε τις εξισώσεις όλων των διαθέσιμων εφαπτομένων της συνάρτησης y = 3 cos 3 2 x - π 4 - 1 3, οι οποίες βρίσκονται κάθετα στην ευθεία y = - 2 x + 1 2.
Λύση
Για τη σύνταξη της εφαπτομενικής εξίσωσης, είναι απαραίτητο να βρούμε τον συντελεστή και τις συντεταγμένες του εφαπτομενικού σημείου, με βάση την συνθήκη της καθετότητας των ευθειών. Ο ορισμός είναι ο εξής: το γινόμενο των γωνιακών συντελεστών που είναι κάθετοι σε ευθείες είναι ίσο με - 1, δηλαδή γράφεται ως k x · k ⊥ = - 1. Από την προϋπόθεση ότι ο γωνιακός συντελεστής βρίσκεται κάθετα στην ευθεία και είναι ίσος με k ⊥ = - 2, τότε k x = - 1 k ⊥ = - 1 - 2 = 1 2.
Τώρα πρέπει να βρείτε τις συντεταγμένες των σημείων επαφής. Πρέπει να βρείτε το x και μετά την τιμή του για μια δεδομένη συνάρτηση. Σημειώστε ότι από τη γεωμετρική σημασία της παραγώγου στο σημείο
x 0 παίρνουμε ότι k x = y "(x 0). Από αυτή την ισότητα βρίσκουμε τις τιμές του x για τα σημεία επαφής.
Το καταλαβαίνουμε
y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - αμαρτία 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 αμαρτία 3 2 x 0 - π 4 3 2 = - 9 2 αμαρτία 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 αμαρτία 3 2 x 0 - π 4 = 1 2 ⇒ αμαρτία 3 2 x 0 - π 4 = - 1 9
Αυτό τριγωνομετρική εξίσωσηθα χρησιμοποιηθεί για τον υπολογισμό των τεταγμένων των εφαπτομένων σημείων.
3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk ή 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk ή 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk ή x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Το Z είναι ένα σύνολο ακεραίων.
x σημεία επαφής έχουν βρεθεί. Τώρα πρέπει να προχωρήσετε στην αναζήτηση των τιμών του y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 ή y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 ή y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 ή y 0 = - 4 5 + 1 3
Από αυτό προκύπτει ότι 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 είναι τα σημεία εφαπτομένης.
Απάντηση:οι απαραίτητες εξισώσεις θα γραφούν ως
y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
Για μια οπτική αναπαράσταση, θεωρήστε μια συνάρτηση και μια εφαπτομένη σε μια γραμμή συντεταγμένων.
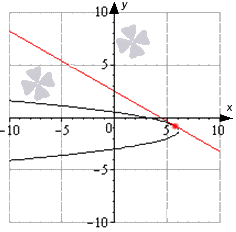
Το σχήμα δείχνει ότι η συνάρτηση βρίσκεται στο διάστημα [ - 10 ; 10 ], όπου η μαύρη γραμμή είναι η γραφική παράσταση της συνάρτησης, οι μπλε γραμμές είναι εφαπτομένες, οι οποίες βρίσκονται κάθετα στη δεδομένη ευθεία της μορφής y = - 2 x + 1 2. Οι κόκκινες κουκκίδες είναι σημεία επαφής.

Οι κανονικές εξισώσεις των καμπυλών 2ης τάξης δεν είναι συναρτήσεις μονής τιμής. Οι εφαπτομενικές εξισώσεις για αυτές καταρτίζονται σύμφωνα με γνωστά σχήματα.
Εφαπτομένη σε κύκλο
Να ορίσετε έναν κύκλο με κέντρο στο σημείο x c e n t e r ; y c e n t e r και την ακτίνα R, εφαρμόστε τον τύπο x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .
Αυτή η ισότητα μπορεί να γραφτεί ως ένωση δύο συναρτήσεων:
y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r
Η πρώτη λειτουργία βρίσκεται στο επάνω μέρος και η δεύτερη στο κάτω μέρος, όπως φαίνεται στο σχήμα.

Να συντάξετε την εξίσωση ενός κύκλου στο σημείο x 0; y 0 , που βρίσκεται στο πάνω ή στο κάτω ημικύκλιο, θα πρέπει να βρείτε την εξίσωση της γραφικής παράστασης μιας συνάρτησης της μορφής y = R 2 - x - x c e n t e r 2 + y c e n t e r ή y = - R 2 - x - x c e n t e r 2 + y c e n t e r στο υποδεικνυόμενο σημείο.
Όταν στα σημεία x c e n t e r ; y c e n t e r + R και x c e n t e r ; Οι εφαπτομένες y c e n t e r - R μπορούν να δοθούν από τις εξισώσεις y = y c e n t e r + R και y = y c e n t e r - R , και στα σημεία x c e n t e r + R ; y c e n t e r και
x c e n t e r - R ; Το y c e n t e r θα είναι παράλληλο με το o y, τότε λαμβάνουμε εξισώσεις της μορφής x = x c e n t e r + R και x = x c e n t e r - R .

Εφαπτομένη σε έλλειψη
Όταν η έλλειψη έχει κέντρο στο x c e n t e r ; y c e n t e r με ημιάξονες a και b, τότε μπορεί να προσδιοριστεί χρησιμοποιώντας την εξίσωση x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.
Μια έλλειψη και ένας κύκλος μπορούν να υποδηλωθούν συνδυάζοντας δύο συναρτήσεις, δηλαδή την άνω και κάτω μισή έλλειψη. Τότε το καταλαβαίνουμε
y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Αν οι εφαπτομένες βρίσκονται στις κορυφές της έλλειψης, τότε είναι παράλληλες περίπου x ή περίπου y. Παρακάτω, για λόγους σαφήνειας, εξετάστε το σχήμα.

Παράδειγμα 6
Γράψτε την εξίσωση της εφαπτομένης στην έλλειψη x - 3 2 4 + y - 5 2 25 = 1 σε σημεία με τιμές x ίσες με x = 2.
Λύση
Είναι απαραίτητο να βρεθούν τα εφαπτομενικά σημεία που αντιστοιχούν στην τιμή x = 2. Αντικαθιστούμε την υπάρχουσα εξίσωση της έλλειψης και το βρίσκουμε
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Τότε 2 ; 5 3 2 + 5 και 2; - 5 3 2 + 5 είναι τα εφαπτομενικά σημεία που ανήκουν στην άνω και κάτω μισή έλλειψη.
Ας προχωρήσουμε στην εύρεση και επίλυση της εξίσωσης της έλλειψης ως προς το y. Το καταλαβαίνουμε
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Προφανώς, η άνω μισή έλλειψη καθορίζεται χρησιμοποιώντας μια συνάρτηση της μορφής y = 5 + 5 2 4 - x - 3 2 και η κάτω μισή έλλειψη y = 5 - 5 2 4 - x - 3 2.
Ας εφαρμόσουμε έναν τυπικό αλγόριθμο για να δημιουργήσουμε μια εξίσωση για μια εφαπτομένη στη γραφική παράσταση μιας συνάρτησης σε ένα σημείο. Ας γράψουμε ότι η εξίσωση για την πρώτη εφαπτομένη στο σημείο 2; Το 5 3 2 + 5 θα μοιάζει
y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Βρίσκουμε ότι η εξίσωση της δεύτερης εφαπτομένης με τιμή στο σημείο
2 ; - Το 5 3 2 + 5 παίρνει τη μορφή
y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Γραφικά, οι εφαπτομένες ορίζονται ως εξής:

Εφαπτομένη στην υπερβολή
Όταν μια υπερβολή έχει κέντρο στο x c e n t e r ; y c e n t e r και κορυφές x c e n t e r + α ; y c e n t e r and x c e n t e r - α ; y c e n t e r , λαμβάνει χώρα η ανισότητα x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, αν με κορυφές x c e n t e r ; y c e n t e r + b και x c e n t e r ; y c e n t e r - b , στη συνέχεια προσδιορίζεται χρησιμοποιώντας την ανισότητα x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Μια υπερβολή μπορεί να αναπαρασταθεί ως δύο συνδυασμένες συναρτήσεις της φόρμας
y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r ή y = b a · (x - x c e n t e r) 2 + a 2 t e r (x - x c e n t e r) 2 + a 2 + y c e n t e r

Στην πρώτη περίπτωση έχουμε ότι οι εφαπτομένες είναι παράλληλες στο y και στη δεύτερη είναι παράλληλες στο x.
Επομένως, για να βρεθεί η εξίσωση της εφαπτομένης σε μια υπερβολή, είναι απαραίτητο να βρεθεί σε ποια συνάρτηση ανήκει το σημείο εφαπτομένης. Για να προσδιοριστεί αυτό, είναι απαραίτητο να αντικαταστήσετε τις εξισώσεις και να ελέγξετε την ταυτότητα.
Παράδειγμα 7
Γράψτε μια εξίσωση για την εφαπτομένη στην υπερβολή x - 3 2 4 - y + 3 2 9 = 1 στο σημείο 7; - 3 3 - 3 .
Λύση
Είναι απαραίτητο να μετασχηματιστεί η εγγραφή λύσης για την εύρεση υπερβολής χρησιμοποιώντας 2 συναρτήσεις. Το καταλαβαίνουμε
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 και y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Είναι απαραίτητο να προσδιοριστεί σε ποια συνάρτηση ανήκει ένα δεδομένο σημείο με συντεταγμένες 7. - 3 3 - 3 .
Προφανώς, για να ελέγξετε την πρώτη συνάρτηση είναι απαραίτητο y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, τότε το σημείο δεν ανήκει στη γραφική παράσταση, αφού η ισότητα δεν ισχύει.
Για τη δεύτερη συνάρτηση έχουμε ότι y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, που σημαίνει ότι το σημείο ανήκει στη δεδομένη γραφική παράσταση. Από εδώ θα πρέπει να βρείτε την πλαγιά.
Το καταλαβαίνουμε
y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Απάντηση:η εφαπτομενική εξίσωση μπορεί να παρασταθεί ως
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Απεικονίζεται ξεκάθαρα ως εξής:

Εφαπτομένη σε παραβολή
Για να δημιουργήσετε μια εξίσωση για την εφαπτομένη στην παραβολή y = a x 2 + b x + c στο σημείο x 0, y (x 0), πρέπει να χρησιμοποιήσετε έναν τυπικό αλγόριθμο, τότε η εξίσωση θα πάρει τη μορφή y = y "(x 0) x - x 0 + y ( x 0). Μια τέτοια εφαπτομένη στην κορυφή είναι παράλληλη προς το x.
Θα πρέπει να ορίσετε την παραβολή x = a y 2 + b y + c ως ένωση δύο συναρτήσεων. Επομένως, πρέπει να λύσουμε την εξίσωση για το y. Το καταλαβαίνουμε
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Γραφικά απεικονίζεται ως:

Για να μάθετε εάν ένα σημείο x 0, y (x 0) ανήκει σε μια συνάρτηση, προχωρήστε απαλά σύμφωνα με τον τυπικό αλγόριθμο. Μια τέτοια εφαπτομένη θα είναι παράλληλη στο o y σε σχέση με την παραβολή.
Παράδειγμα 8
Να γράψετε την εξίσωση της εφαπτομένης στη γραφική παράσταση x - 2 y 2 - 5 y + 3 όταν έχουμε γωνία εφαπτομένης 150 °.
Λύση
Ξεκινάμε τη λύση αναπαραστώντας την παραβολή ως δύο συναρτήσεις. Το καταλαβαίνουμε
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
Η τιμή της κλίσης είναι ίση με την τιμή της παραγώγου στο σημείο x 0 αυτής της συνάρτησης και είναι ίση με την εφαπτομένη της γωνίας κλίσης.
Παίρνουμε:
k x = y "(x 0) = t g α x = t g 150 ° = - 1 3
Από εδώ προσδιορίζουμε την τιμή x για τα σημεία επαφής.
Η πρώτη συνάρτηση θα γραφτεί ως
y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Προφανώς δεν υπάρχουν πραγματικές ρίζες, αφού πήραμε αρνητική τιμή. Συμπεραίνουμε ότι δεν υπάρχει εφαπτομένη με γωνία 150° για μια τέτοια συνάρτηση.
Η δεύτερη συνάρτηση θα γραφτεί ως
y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Έχουμε ότι τα σημεία επαφής είναι 23 4 ; - 5 + 3 4 .
Απάντηση:η εφαπτομενική εξίσωση παίρνει τη μορφή
y = - 1 3 x - 23 4 + - 5 + 3 4
Ας το απεικονίσουμε γραφικά ως εξής:
Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
Στο θέμα «Ο γωνιακός συντελεστής μιας εφαπτομένης ως η εφαπτομένη της γωνίας κλίσης» δίνονται αρκετές εργασίες στην εξέταση πιστοποίησης. Ανάλογα με την κατάστασή τους, ο απόφοιτος μπορεί να κληθεί να δώσει είτε μια πλήρη απάντηση είτε μια σύντομη απάντηση. Όταν προετοιμάζεται να δώσει την Εξέταση του Ενιαίου Κράτους στα μαθηματικά, ο μαθητής πρέπει οπωσδήποτε να επαναλάβει τις εργασίες που απαιτούν τον υπολογισμό της κλίσης μιας εφαπτομένης.
Θα σας βοηθήσει να το κάνετε αυτό εκπαιδευτική πύλη«Σκολκόβο». Οι ειδικοί μας ετοίμασαν και παρουσίασαν θεωρητικό και πρακτικό υλικό με τον πιο προσιτό δυνατό τρόπο. Έχοντας εξοικειωθεί με αυτό, οι απόφοιτοι με οποιοδήποτε επίπεδο εκπαίδευσης θα είναι σε θέση να λύσουν με επιτυχία προβλήματα που σχετίζονται με παράγωγα στα οποία είναι απαραίτητο να βρεθεί η εφαπτομένη της εφαπτομένης γωνίας.
Βασικές στιγμές
Για να βρείτε το σωστό και ορθολογική απόφασηΓια παρόμοιες εργασίες στο Unified State Exam, πρέπει να θυμάστε τον βασικό ορισμό: η παράγωγος αντιπροσωπεύει το ρυθμό αλλαγής μιας συνάρτησης. ισούται με την εφαπτομένη της εφαπτομένης γωνίας που χαράσσεται στη γραφική παράσταση της συνάρτησης σε ένα ορισμένο σημείο. Είναι εξίσου σημαντικό να ολοκληρώσετε το σχέδιο. Θα σας επιτρέψει να βρείτε σωστή λύση Προβλήματα Ενιαίας Κρατικής Εξέτασηςστην παράγωγο, στην οποία είναι απαραίτητο να υπολογιστεί η εφαπτομένη της εφαπτομένης γωνίας. Για λόγους σαφήνειας, είναι καλύτερο να σχεδιάσετε το γράφημα στο επίπεδο OXY.
Εάν έχετε ήδη εξοικειωθεί με το βασικό υλικό για το θέμα των παραγώγων και είστε έτοιμοι να ξεκινήσετε την επίλυση προβλημάτων σχετικά με τον υπολογισμό της εφαπτομένης της γωνίας της εφαπτομένης, όπως π.χ. Εργασίες Ενιαίας Κρατικής Εξετάσεων, μπορείτε να το κάνετε διαδικτυακά. Για κάθε εργασία, για παράδειγμα, προβλήματα σχετικά με το θέμα «Σχέση μιας παραγώγου με την ταχύτητα και την επιτάχυνση ενός σώματος», καταγράψαμε τη σωστή απάντηση και τον αλγόριθμο λύσης. Ταυτόχρονα, οι μαθητές μπορούν να εξασκηθούν στην ολοκλήρωση εργασιών διάφορα επίπεδαδυσκολίες. Εάν είναι απαραίτητο, η άσκηση μπορεί να αποθηκευτεί στην ενότητα "Αγαπημένα", ώστε να συζητήσετε τη λύση με τον δάσκαλο αργότερα.
Η διατήρηση του απορρήτου σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε τις πρακτικές απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.
Συλλογή και χρήση προσωπικών πληροφοριών
Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την αναγνώριση ή επικοινωνία με ένα συγκεκριμένο άτομο.
Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.
Ακολουθούν ορισμένα παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.
Ποιες προσωπικές πληροφορίες συλλέγουμε:
- Όταν υποβάλλετε μια αίτηση στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, όπως το όνομά σας, τον αριθμό τηλεφώνου, τη διεύθυνσή σας ΗΛΕΚΤΡΟΝΙΚΗ ΔΙΕΥΘΥΝΣΗκαι τα λοιπά.
Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:
- Συλλέγεται από εμάς προσωπικές πληροφορίεςμας επιτρέπει να επικοινωνήσουμε μαζί σας και να σας ενημερώσουμε για μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
- Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να στείλουμε σημαντικές ειδοποιήσεις και επικοινωνίες.
- Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
- Εάν συμμετέχετε σε κλήρωση, διαγωνισμό ή παρόμοια προσφορά, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.
Αποκάλυψη πληροφοριών σε τρίτους
Δεν αποκαλύπτουμε τις πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.
Εξαιρέσεις:
- Εάν είναι απαραίτητο - σύμφωνα με το νόμο, τη δικαστική διαδικασία, τις νομικές διαδικασίες ή/και με βάση δημόσια αιτήματα ή αιτήματα από κυβερνητικές υπηρεσίεςστο έδαφος της Ρωσικής Ομοσπονδίας - αποκαλύψτε τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι αυτή η αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους σκοπούς δημόσιας σημασίας.
- Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τις προσωπικές πληροφορίες που συλλέγουμε στον αντίστοιχο τρίτο διάδοχο.
Προστασία προσωπικών πληροφοριών
Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κακή χρήση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.
Σεβασμός του απορρήτου σας σε εταιρικό επίπεδο
Για να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, κοινοποιούμε τα πρότυπα απορρήτου και ασφάλειας στους υπαλλήλους μας και εφαρμόζουμε αυστηρά τις πρακτικές απορρήτου.
Σε αυτό το άρθρο θα αναλύσουμε όλους τους τύπους προβλημάτων για να βρούμε
Ας θυμηθούμε γεωμετρική σημασία της παραγώγου: αν μια εφαπτομένη σχεδιάζεται στη γραφική παράσταση μιας συνάρτησης σε ένα σημείο, τότε ο συντελεστής κλίσης της εφαπτομένης (ίσος με την εφαπτομένη της γωνίας μεταξύ της εφαπτομένης και της θετικής κατεύθυνσης του άξονα) είναι ίσος με την παράγωγο της συνάρτησης στο σημείο.


Ας πάρουμε ένα αυθαίρετο σημείο στην εφαπτομένη με συντεταγμένες:

Και σκεφτείτε ένα ορθογώνιο τρίγωνο:

Σε αυτό το τρίγωνο 
Από εδώ 

Αυτή είναι η εξίσωση της εφαπτομένης που σχεδιάζεται στη γραφική παράσταση της συνάρτησης στο σημείο.
Για να γράψουμε την εξίσωση της εφαπτομένης, χρειάζεται μόνο να γνωρίζουμε την εξίσωση της συνάρτησης και το σημείο στο οποίο σχεδιάζεται η εφαπτομένη. Τότε μπορούμε να βρούμε και .
Υπάρχουν τρεις κύριοι τύποι προβλημάτων εξίσωσης εφαπτομένων.
1. Δίνεται ένα σημείο επαφής
2. Δίνεται ο συντελεστής της εφαπτομένης κλίσης, δηλαδή η τιμή της παραγώγου της συνάρτησης στο σημείο.
3. Δίνονται οι συντεταγμένες του σημείου από το οποίο σύρεται η εφαπτομένη, αλλά που δεν είναι το σημείο εφαπτομένης.
Ας δούμε κάθε τύπο εργασίας.
1 . Να γράψετε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης ![]() στο σημείο .
στο σημείο .
![]() .
.
β) Να βρείτε την τιμή της παραγώγου στο σημείο . Αρχικά ας βρούμε την παράγωγο της συνάρτησης
![]()
![]()
Ας αντικαταστήσουμε τις τιμές που βρέθηκαν στην εφαπτομενική εξίσωση:
![]()
Ας ανοίξουμε τις αγκύλες στη δεξιά πλευρά της εξίσωσης. Παίρνουμε:
Απάντηση: .
2. Να βρείτε την τετμημένη των σημείων στα οποία οι συναρτήσεις εφάπτονται στη γραφική παράσταση ![]() παράλληλα με τον άξονα x.
παράλληλα με τον άξονα x.
Εάν η εφαπτομένη είναι παράλληλη προς τον άξονα x, επομένως η γωνία μεταξύ της εφαπτομένης και της θετικής κατεύθυνσης του άξονα είναι μηδέν, επομένως η εφαπτομένη της εφαπτομένης γωνίας είναι μηδέν. Αυτό σημαίνει ότι η τιμή της παραγώγου της συνάρτησης ![]() στα σημεία επαφής είναι μηδέν.
στα σημεία επαφής είναι μηδέν.
α) Να βρείτε την παράγωγο της συνάρτησης ![]() .
.
![]()
β) Ας εξισώσουμε την παράγωγο με το μηδέν και ας βρούμε τις τιμές στις οποίες η εφαπτομένη είναι παράλληλη στον άξονα:
![]()

Εξισώνοντας κάθε παράγοντα με μηδέν, παίρνουμε:
Απάντηση: 0;3;5
3. Να γράψετε εξισώσεις για τις εφαπτομένες στη γραφική παράσταση μιας συνάρτησης , παράλληλο ευθεία .
Μια εφαπτομένη είναι παράλληλη σε μια ευθεία. Η κλίση αυτής της γραμμής είναι -1. Εφόσον η εφαπτομένη είναι παράλληλη σε αυτήν την ευθεία, επομένως, η κλίση της εφαπτομένης είναι επίσης -1. Αυτό είναι γνωρίζουμε την κλίση της εφαπτομένης, και ως εκ τούτου, παράγωγη τιμή στο σημείο εφαπτομένης.
Αυτός είναι ο δεύτερος τύπος προβλήματος για την εύρεση της εφαπτομένης εξίσωσης.
Έτσι, μας δίνεται η συνάρτηση και η τιμή της παραγώγου στο σημείο εφαπτομένης.
α) Να βρείτε τα σημεία στα οποία η παράγωγος της συνάρτησης είναι ίση με -1.
Αρχικά, ας βρούμε την εξίσωση της παραγώγου.

Ας εξισώσουμε την παράγωγο με τον αριθμό -1.

Ας βρούμε την τιμή της συνάρτησης στο σημείο.
![]()
(κατά συνθήκη)
![]() .
.
β) Να βρείτε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης στο σημείο .
Ας βρούμε την τιμή της συνάρτησης στο σημείο.
![]()
(κατά συνθήκη).
Ας αντικαταστήσουμε αυτές τις τιμές στην εφαπτομενική εξίσωση:
![]() .
.
Απάντηση:
4 . Να γράψετε την εξίσωση της εφαπτομένης της καμπύλης , περνώντας από ένα σημείο
Αρχικά, ας ελέγξουμε αν το σημείο είναι εφαπτομενικό. Αν ένα σημείο είναι εφαπτομενικό, τότε ανήκει στη γραφική παράσταση της συνάρτησης και οι συντεταγμένες του πρέπει να ικανοποιούν την εξίσωση της συνάρτησης. Ας αντικαταστήσουμε τις συντεταγμένες του σημείου στην εξίσωση της συνάρτησης.
Title="1sqrt(8-3^2)">. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и !} δεν είναι σημείο επαφής.
Αυτός είναι ο τελευταίος τύπος προβλήματος για την εύρεση της εφαπτομένης εξίσωσης. Το πρώτο πράγμα πρέπει να βρούμε την τετμημένη του εφαπτομενικού σημείου.
Ας βρούμε την τιμή.
Ας είναι το σημείο επαφής. Το σημείο ανήκει στην εφαπτομένη της γραφικής παράστασης της συνάρτησης. Αν αντικαταστήσουμε τις συντεταγμένες αυτού του σημείου στην εφαπτομενική εξίσωση, θα έχουμε τη σωστή ισότητα:
 .
.
Η τιμή της συνάρτησης σε ένα σημείο είναι  .
.
Ας βρούμε την τιμή της παραγώγου της συνάρτησης στο σημείο.
Αρχικά, ας βρούμε την παράγωγο της συνάρτησης. Αυτό .

Η παράγωγος σε ένα σημείο είναι ίση με  .
.
Ας αντικαταστήσουμε τις εκφράσεις για και στην εφαπτομενική εξίσωση. Παίρνουμε την εξίσωση για:

Ας λύσουμε αυτή την εξίσωση.
Μειώστε τον αριθμητή και τον παρονομαστή του κλάσματος κατά 2:

Ας φέρουμε τη δεξιά πλευρά της εξίσωσης σε έναν κοινό παρονομαστή. Παίρνουμε:

Ας απλοποιήσουμε τον αριθμητή του κλάσματος και ας πολλαπλασιάσουμε και τις δύο πλευρές με - αυτή η έκφραση είναι αυστηρά μεγαλύτερη από το μηδέν.
Παίρνουμε την εξίσωση

Ας το λύσουμε. Για να γίνει αυτό, ας τετραγωνίσουμε και τα δύο μέρη και ας προχωρήσουμε στο σύστημα.
Title="delim(lbrace)(matrix(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0 ) ))( )">!}
Ας λύσουμε την πρώτη εξίσωση.
![]()
![]()
Ας αποφασίσουμε τετραγωνική εξίσωση, παίρνουμε
Η δεύτερη ρίζα δεν ικανοποιεί την προϋπόθεση title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}
Ας γράψουμε την εξίσωση της εφαπτομένης της καμπύλης στο σημείο. Για να το κάνετε αυτό, αντικαταστήστε την τιμή στην εξίσωση  - Το ηχογραφήσαμε ήδη.
- Το ηχογραφήσαμε ήδη.

![]()
Απάντηση:
.
Οδηγίες
Προσδιορίζουμε τον γωνιακό συντελεστή της εφαπτομένης στην καμπύλη στο σημείο Μ.
Η καμπύλη που αντιπροσωπεύει τη γραφική παράσταση της συνάρτησης y = f(x) είναι συνεχής σε μια ορισμένη γειτονιά του σημείου Μ (συμπεριλαμβανομένου του ίδιου του σημείου Μ).
Εάν η τιμή f‘(x0) δεν υπάρχει, τότε είτε δεν υπάρχει εφαπτομένη, είτε τρέχει κατακόρυφα. Υπό το πρίσμα αυτό, η παρουσία παραγώγου της συνάρτησης στο σημείο x0 οφείλεται στην ύπαρξη μιας μη κατακόρυφης εφαπτομένης στη γραφική παράσταση της συνάρτησης στο σημείο (x0, f(x0)). Σε αυτή την περίπτωση, ο γωνιακός συντελεστής της εφαπτομένης θα είναι ίσος με f "(x0). Έτσι, η γεωμετρική σημασία της παραγώγου γίνεται σαφής - ο υπολογισμός του γωνιακού συντελεστή της εφαπτομένης.
Βρείτε την τιμή της τετμημένης του εφαπτομενικού σημείου, που συμβολίζεται με το γράμμα «a». Αν συμπίπτει με ένα δεδομένο σημείο εφαπτομένης, τότε το "a" θα είναι η συντεταγμένη του x. Προσδιορίστε την τιμή λειτουργίεςστ(α) με αντικατάσταση στην εξίσωση λειτουργίεςτιμή τετμημένης.
Να προσδιορίσετε την πρώτη παράγωγο της εξίσωσης λειτουργίες f'(x) και αντικαταστήστε την τιμή του σημείου "a" σε αυτό.
Παίρνω γενική εξίσωσηεφαπτομένη, η οποία ορίζεται ως y = f(a) = f (a)(x – a) και αντικαθιστούν τις τιμές που βρέθηκαν των a, f(a), f "(a) σε αυτήν. θα βρεθεί η λύση της γραφικής παράστασης και της εφαπτομένης.
Λύστε το πρόβλημα με διαφορετικό τρόπο αν το δεδομένο σημείο εφαπτομένης δεν συμπίπτει με το σημείο εφαπτομένης. Σε αυτή την περίπτωση, είναι απαραίτητο να αντικαταστήσουμε το «a» αντί για αριθμούς στην εφαπτομενική εξίσωση. Μετά από αυτό, αντί για τα γράμματα "x" και "y", αντικαταστήστε την τιμή συντεταγμένων δεδομένο σημείο. Να λύσετε την εξίσωση που προκύπτει στην οποία το "a" είναι το άγνωστο. Συνδέστε την τιμή που προκύπτει στην εφαπτομενική εξίσωση.
Γράψτε μια εξίσωση για μια εφαπτομένη με το γράμμα "a" εάν η δήλωση προβλήματος καθορίζει την εξίσωση λειτουργίεςκαι την εξίσωση μιας παράλληλης ευθείας σε σχέση με την επιθυμητή εφαπτομένη. Μετά από αυτό χρειαζόμαστε την παράγωγο λειτουργίες, στη συντεταγμένη στο σημείο «α». Αντικαταστήστε την κατάλληλη τιμή στην εφαπτομενική εξίσωση και λύστε τη συνάρτηση.

