Μια από τις σημαντικότερες επιστήμες, η εφαρμογή της οποίας μπορεί να παρατηρηθεί σε κλάδους όπως η χημεία, η φυσική, ακόμη και η βιολογία, είναι τα μαθηματικά. Η μελέτη αυτής της επιστήμης σάς επιτρέπει να αναπτύξετε ορισμένες ψυχικές ιδιότητες και να βελτιώσετε την ικανότητά σας να συγκεντρώνεστε. Ένα από τα θέματα που αξίζουν ιδιαίτερης προσοχής στο μάθημα των Μαθηματικών είναι η πρόσθεση και η αφαίρεση κλασμάτων. Πολλοί μαθητές δυσκολεύονται να μελετήσουν. Ίσως το άρθρο μας θα σας βοηθήσει να κατανοήσετε καλύτερα αυτό το θέμα.

Πώς να αφαιρέσετε τα κλάσματα των οποίων οι παρονομαστές είναι ίδιοι

Τα κλάσματα είναι οι ίδιοι αριθμοί με τους οποίους μπορείτε να παράγετε διάφορες δράσεις. Η διαφορά τους από τους ακέραιους αριθμούς έγκειται στην παρουσία ενός παρονομαστή. Αυτός είναι ο λόγος για τον οποίο, όταν εκτελείτε πράξεις με κλάσματα, πρέπει να μελετήσετε ορισμένα από τα χαρακτηριστικά και τους κανόνες τους. Πλέον απλή υπόθεσηείναι η αφαίρεση συνηθισμένων κλασμάτων των οποίων οι παρονομαστές παριστάνονται ως ο ίδιος αριθμός. Η εκτέλεση αυτής της ενέργειας δεν θα είναι δύσκολη εάν γνωρίζετε έναν απλό κανόνα:

• Για να αφαιρέσουμε ένα δευτερόλεπτο από ένα κλάσμα, είναι απαραίτητο να αφαιρέσουμε τον αριθμητή του αφαιρούμενου κλάσματος από τον αριθμητή του κλάσματος που ανάγεται. Γράφουμε αυτόν τον αριθμό στον αριθμητή της διαφοράς και αφήνουμε τον παρονομαστή ίδιο: k/m - b/m = (k-b)/m.

Παραδείγματα αφαίρεσης κλασμάτων των οποίων οι παρονομαστές είναι ίδιοι

7/19 - 3/19 = (7 - 3)/19 = 4/19.

Από τον αριθμητή του κλάσματος "7" αφαιρούμε τον αριθμητή του κλάσματος "3" που πρέπει να αφαιρεθεί, παίρνουμε "4". Γράφουμε αυτόν τον αριθμό στον αριθμητή της απάντησης και στον παρονομαστή βάζουμε τον ίδιο αριθμό που ήταν στους παρονομαστές του πρώτου και του δεύτερου κλάσματος - "19".

Η παρακάτω εικόνα δείχνει πολλά ακόμη παρόμοια παραδείγματα.

Ας εξετάσουμε ένα πιο σύνθετο παράδειγμα όπου τα κλάσματα με παρονομαστές αφαιρούνται:

29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7)/47 = 9/47.

Από τον αριθμητή του κλάσματος "29" που μειώνεται αφαιρώντας με τη σειρά τους τους αριθμητές όλων των επόμενων κλασμάτων - "3", "8", "2", "7". Ως αποτέλεσμα, παίρνουμε το αποτέλεσμα "9", το οποίο σημειώνουμε στον αριθμητή της απάντησης και στον παρονομαστή σημειώνουμε τον αριθμό που βρίσκεται στους παρονομαστές όλων αυτών των κλασμάτων - "47".

Προσθήκη κλασμάτων που έχουν τον ίδιο παρονομαστή

Η πρόσθεση και η αφαίρεση συνηθισμένων κλασμάτων ακολουθεί την ίδια αρχή.

• Για να προσθέσετε κλάσματα των οποίων οι παρονομαστές είναι ίδιοι, πρέπει να προσθέσετε τους αριθμητές. Ο αριθμός που προκύπτει είναι ο αριθμητής του αθροίσματος και ο παρονομαστής θα παραμείνει ο ίδιος: k/m + b/m = (k + b)/m.

Ας δούμε πώς φαίνεται αυτό χρησιμοποιώντας ένα παράδειγμα:

1/4 + 2/4 = 3/4.

Στον αριθμητή του πρώτου όρου του κλάσματος - "1" - προσθέστε τον αριθμητή του δεύτερου όρου του κλάσματος - "2". Το αποτέλεσμα - "3" - γράφεται στον αριθμητή του αθροίσματος και ο παρονομαστής παραμένει ο ίδιος με αυτόν που υπάρχει στα κλάσματα - "4".

Κλάσματα με διαφορετικούς παρονομαστές και η αφαίρεση τους

Έχουμε ήδη εξετάσει την πράξη με κλάσματα που έχουν τον ίδιο παρονομαστή. Όπως βλέπουμε, γνωρίζοντας απλούς κανόνες, η επίλυση τέτοιων παραδειγμάτων είναι αρκετά εύκολη. Τι γίνεται όμως αν χρειαστεί να εκτελέσετε μια πράξη με κλάσματα που έχουν διαφορετικούς παρονομαστές; Πολλοί μαθητές δευτεροβάθμιας εκπαίδευσης μπερδεύονται με τέτοια παραδείγματα. Αλλά και εδώ, αν γνωρίζετε την αρχή της λύσης, τα παραδείγματα δεν θα σας δυσκολεύουν πλέον. Υπάρχει επίσης ένας κανόνας εδώ, χωρίς τον οποίο η επίλυση τέτοιων κλασμάτων είναι απλά αδύνατη.

Για να αφαιρέσετε κλάσματα από διαφορετικούς παρονομαστές, είναι απαραίτητο να τα μειώσετε στον ίδιο χαμηλότερο παρονομαστή.



Θα μιλήσουμε λεπτομερέστερα για το πώς να το κάνουμε αυτό.

Ιδιότητα κλάσματος

Για να φέρετε πολλά κλάσματα στον ίδιο παρονομαστή, πρέπει να χρησιμοποιήσετε την κύρια ιδιότητα ενός κλάσματος στη λύση: αφού διαιρέσετε ή πολλαπλασιάσετε τον αριθμητή και τον παρονομαστή με τον ίδιο αριθμό, παίρνετε ένα κλάσμα ίσο με το δεδομένο.

Έτσι, για παράδειγμα, το κλάσμα 2/3 μπορεί να έχει παρονομαστές όπως «6», «9», «12» κ.λπ., δηλαδή μπορεί να έχει τη μορφή οποιουδήποτε αριθμού που είναι πολλαπλάσιο του «3». Αφού πολλαπλασιάσουμε τον αριθμητή και τον παρονομαστή με το "2", παίρνουμε το κλάσμα 4/6. Αφού πολλαπλασιάσουμε τον αριθμητή και τον παρονομαστή του αρχικού κλάσματος με το "3", παίρνουμε 6/9 και αν κάνουμε παρόμοια πράξη με τον αριθμό "4", παίρνουμε 8/12. Μια ισότητα μπορεί να γραφτεί ως εξής:

2/3 = 4/6 = 6/9 = 8/12…

Πώς να μετατρέψετε πολλά κλάσματα στον ίδιο παρονομαστή

Ας δούμε πώς να μειώσουμε πολλαπλά κλάσματα στον ίδιο παρονομαστή. Για παράδειγμα, ας πάρουμε τα κλάσματα που φαίνονται στην παρακάτω εικόνα. Πρώτα πρέπει να προσδιορίσετε ποιος αριθμός μπορεί να γίνει παρονομαστής για όλους. Για να διευκολύνουμε τα πράγματα, ας παραγοντοποιήσουμε τους υπάρχοντες παρονομαστές.

Ο παρονομαστής του κλάσματος 1/2 και του κλάσματος 2/3 δεν μπορεί να παραγοντοποιηθεί. Ο παρονομαστής 7/9 έχει δύο παράγοντες 7/9 = 7/(3 x 3), τον παρονομαστή του κλάσματος 5/6 = 5/(2 x 3). Τώρα πρέπει να προσδιορίσουμε ποιοι παράγοντες θα είναι οι μικρότεροι και για αυτά τα τέσσερα κλάσματα. Εφόσον το πρώτο κλάσμα έχει τον αριθμό «2» στον παρονομαστή, σημαίνει ότι πρέπει να υπάρχει σε όλους τους παρονομαστές· στο κλάσμα 7/9 υπάρχουν δύο τριάδες, που σημαίνει ότι και οι δύο πρέπει να υπάρχουν στον παρονομαστή. Λαμβάνοντας υπόψη τα παραπάνω, προσδιορίζουμε ότι ο παρονομαστής αποτελείται από τρεις παράγοντες: 3, 2, 3 και ισούται με 3 x 2 x 3 = 18.



Ας εξετάσουμε το πρώτο κλάσμα - 1/2. Υπάρχει ένα "2" στον παρονομαστή του, αλλά δεν υπάρχει ένα μόνο "3" ψηφίο, αλλά θα πρέπει να είναι δύο. Για να γίνει αυτό, πολλαπλασιάζουμε τον παρονομαστή με δύο τριπλάσια, αλλά, σύμφωνα με την ιδιότητα ενός κλάσματος, πρέπει να πολλαπλασιάσουμε τον αριθμητή με δύο τριπλάσια:
1/2 = (1 x 3 x 3)/(2 x 3 x 3) = 9/18.

Κάνουμε τις ίδιες πράξεις με τα υπόλοιπα κλάσματα.

• 2/3 - ένα τρία και ένα δύο λείπουν στον παρονομαστή:
  2/3 = (2 x 3 x 2)/(3 x 3 x 2) = 12/18.
• 7/9 ή 7/(3 x 3) - ο παρονομαστής λείπει δύο:
  7/9 = (7 x 2)/(9 x 2) = 14/18.
• 5/6 ή 5/(2 x 3) - στον παρονομαστή λείπει ένα τρία:
  5/6 = (5 x 3)/(6 x 3) = 15/18.

Όλα μαζί μοιάζει με αυτό:



Πώς να αφαιρέσετε και να προσθέσετε κλάσματα που έχουν διαφορετικούς παρονομαστές

Όπως αναφέρθηκε παραπάνω, για να προσθέσετε ή να αφαιρέσετε κλάσματα που έχουν διαφορετικούς παρονομαστές, πρέπει να αναχθούν στον ίδιο παρονομαστή και στη συνέχεια να χρησιμοποιήσετε τους κανόνες για την αφαίρεση κλασμάτων που έχουν τον ίδιο παρονομαστή, που έχουν ήδη συζητηθεί.

Ας το δούμε αυτό ως παράδειγμα: 18/4 - 15/3.

Βρίσκοντας το πολλαπλάσιο των αριθμών 18 και 15:

• Ο αριθμός 18 αποτελείται από 3 x 2 x 3.
• Ο αριθμός 15 αποτελείται από 5 x 3.
• Το κοινό πολλαπλάσιο θα είναι οι ακόλουθοι παράγοντες: 5 x 3 x 3 x 2 = 90.

Αφού βρεθεί ο παρονομαστής, είναι απαραίτητο να υπολογιστεί ο παράγοντας που θα είναι διαφορετικός για κάθε κλάσμα, δηλαδή ο αριθμός με τον οποίο θα χρειαστεί να πολλαπλασιαστεί όχι μόνο ο παρονομαστής, αλλά και ο αριθμητής. Για να γίνει αυτό, διαιρούμε τον αριθμό που βρήκαμε (το κοινό πολλαπλάσιο) με τον παρονομαστή του κλάσματος για το οποίο πρέπει να καθοριστούν πρόσθετοι παράγοντες.

• 90 διαιρούμενο με 15. Ο αριθμός "6" που προκύπτει θα είναι πολλαπλασιαστής για το 3/15.
• 90 διαιρούμενο με 18. Ο αριθμός "5" που προκύπτει θα είναι πολλαπλασιαστής για το 4/18.

Το επόμενο στάδιο της επίλυσής μας είναι να μειώσουμε κάθε κλάσμα στον παρονομαστή "90".

Έχουμε ήδη μιλήσει για το πώς γίνεται αυτό. Ας δούμε πώς γράφεται αυτό σε ένα παράδειγμα:

(4 x 5)/(18 x 5) - (3 x 6)/(15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.

Εάν τα κλάσματα έχουν μικρούς αριθμούς, τότε μπορείτε να προσδιορίσετε τον κοινό παρονομαστή, όπως στο παράδειγμα που φαίνεται στην παρακάτω εικόνα.



Το ίδιο ισχύει και για όσους έχουν διαφορετικούς παρονομαστές.

Αφαίρεση και έχοντας ακέραια μέρη

Έχουμε ήδη συζητήσει λεπτομερώς την αφαίρεση των κλασμάτων και την πρόσθεσή τους. Αλλά πώς να αφαιρέσετε εάν ένα κλάσμα έχει ένα ακέραιο μέρος; Και πάλι, ας χρησιμοποιήσουμε μερικούς κανόνες:

• Να μετατρέψετε όλα τα κλάσματα που έχουν ακέραιο μέρος σε ακατάλληλα. Ομιλία με απλά λόγια, αφαιρέστε ολόκληρο το τμήμα. Για να το κάνετε αυτό, πολλαπλασιάστε τον αριθμό του ακέραιου μέρους με τον παρονομαστή του κλάσματος και προσθέστε το γινόμενο που προκύπτει στον αριθμητή. Ο αριθμός που βγαίνει μετά από αυτές τις ενέργειες είναι ο αριθμητής του ακατάλληλου κλάσματος. Ο παρονομαστής παραμένει αμετάβλητος.
• Εάν τα κλάσματα έχουν διαφορετικούς παρονομαστές, θα πρέπει να ανάγονται στον ίδιο παρονομαστή.
• Εκτελέστε πρόσθεση ή αφαίρεση με τους ίδιους παρονομαστές.
• Όταν λαμβάνετε ένα ακατάλληλο κλάσμα, επιλέξτε ολόκληρο το τμήμα.



Υπάρχει ένας άλλος τρόπος με τον οποίο μπορείτε να προσθέσετε και να αφαιρέσετε κλάσματα με ολόκληρα μέρη. Για να γίνει αυτό, οι ενέργειες εκτελούνται χωριστά με ολόκληρα μέρη και οι ενέργειες με κλάσματα χωριστά και τα αποτελέσματα καταγράφονται μαζί.



Το παράδειγμα που δίνεται αποτελείται από κλάσματα που έχουν τον ίδιο παρονομαστή. Στην περίπτωση που οι παρονομαστές είναι διαφορετικοί, πρέπει να φέρουν την ίδια τιμή και στη συνέχεια να εκτελέσετε τις ενέργειες όπως φαίνεται στο παράδειγμα.

Αφαίρεση κλασμάτων από ακέραιους αριθμούς

Ένας άλλος τύπος πράξης με κλάσματα είναι η περίπτωση που πρέπει να αφαιρεθεί ένα κλάσμα Εκ πρώτης όψεως, ένα τέτοιο παράδειγμα φαίνεται δύσκολο να λυθεί. Ωστόσο, όλα είναι πολύ απλά εδώ. Για να το λύσετε, πρέπει να μετατρέψετε τον ακέραιο σε κλάσμα και με τον ίδιο παρονομαστή που βρίσκεται στο αφαιρούμενο κλάσμα. Στη συνέχεια, εκτελούμε μια αφαίρεση παρόμοια με την αφαίρεση με ίδιους παρονομαστές. Σε ένα παράδειγμα μοιάζει με αυτό:

7 - 4/9 = (7 x 9)/9 - 4/9 = 53/9 - 4/9 = 49/9.

Η αφαίρεση των κλασμάτων (βαθμός 6) που παρουσιάζεται σε αυτό το άρθρο είναι η βάση για την επίλυση πιο περίπλοκων παραδειγμάτων που καλύπτονται σε επόμενους βαθμούς. Η γνώση αυτού του θέματος χρησιμοποιείται στη συνέχεια για την επίλυση συναρτήσεων, παραγώγων και ούτω καθεξής. Επομένως, είναι πολύ σημαντικό να κατανοήσουμε και να κατανοήσουμε τις πράξεις με τα κλάσματα που συζητήθηκαν παραπάνω.

Τα κλάσματα είναι συνηθισμένοι αριθμοί και μπορούν επίσης να προστεθούν και να αφαιρεθούν. Επειδή όμως έχουν παρονομαστή, απαιτούν πιο περίπλοκους κανόνες από ό,τι για τους ακέραιους.

Ας εξετάσουμε την απλούστερη περίπτωση, όταν υπάρχουν δύο κλάσματα με τους ίδιους παρονομαστές. Επειτα:

Για να προσθέσετε κλάσματα με τους ίδιους παρονομαστές, πρέπει να προσθέσετε τους αριθμητές τους και να αφήσετε τον παρονομαστή αμετάβλητο.

Για να αφαιρέσετε κλάσματα με τους ίδιους παρονομαστές, πρέπει να αφαιρέσετε τον αριθμητή του δεύτερου από τον αριθμητή του πρώτου κλάσματος και να αφήσετε ξανά τον παρονομαστή αμετάβλητο.

Μέσα σε κάθε παράσταση, οι παρονομαστές των κλασμάτων είναι ίσοι. Με τον ορισμό της πρόσθεσης και της αφαίρεσης κλασμάτων παίρνουμε:

Όπως μπορείτε να δείτε, δεν είναι τίποτα περίπλοκο: απλώς προσθέτουμε ή αφαιρούμε τους αριθμητές και αυτό είναι.

Αλλά και σε τέτοια απλές ενέργειεςοι άνθρωποι καταφέρνουν να κάνουν λάθη. Αυτό που ξεχνιέται πιο συχνά είναι ότι ο παρονομαστής δεν αλλάζει. Για παράδειγμα, όταν τα προσθέτουν, αρχίζουν επίσης να αθροίζονται, και αυτό είναι βασικά λάθος.

Ξεφορτώνομαι κακή συνήθειαΗ προσθήκη των παρονομαστών είναι αρκετά απλή. Δοκιμάστε το ίδιο πράγμα κατά την αφαίρεση. Ως αποτέλεσμα, ο παρονομαστής θα είναι μηδέν και το κλάσμα θα χάσει (ξαφνικά!) το νόημά του.

Επομένως, θυμηθείτε μια για πάντα: κατά την πρόσθεση και την αφαίρεση, ο παρονομαστής δεν αλλάζει!

Πολλοί άνθρωποι κάνουν επίσης λάθη όταν προσθέτουν πολλά αρνητικά κλάσματα. Υπάρχει σύγχυση με τα σημάδια: πού να βάλετε ένα μείον και πού να βάλετε ένα συν.

Αυτό το πρόβλημα είναι επίσης πολύ εύκολο να λυθεί. Αρκεί να θυμόμαστε ότι το μείον πριν από το πρόσημο ενός κλάσματος μπορεί πάντα να μεταφερθεί στον αριθμητή - και αντίστροφα. Και φυσικά, μην ξεχνάτε δύο απλούς κανόνες:

1. Συν με πλην δινει πλην?
2. Δύο αρνητικά κάνουν ένα καταφατικό.

Ας τα δούμε όλα αυτά με συγκεκριμένα παραδείγματα:

Εργο. Βρείτε το νόημα της έκφρασης:

Στην πρώτη περίπτωση, όλα είναι απλά, αλλά στη δεύτερη, ας προσθέσουμε μείον στους αριθμητές των κλασμάτων:

Τι να κάνετε εάν οι παρονομαστές είναι διαφορετικοί

Δεν μπορείτε να προσθέσετε κλάσματα με διαφορετικούς παρονομαστές απευθείας. Τουλάχιστον, αυτή η μέθοδος είναι άγνωστη σε μένα. Ωστόσο, τα αρχικά κλάσματα μπορούν πάντα να ξαναγραφούν έτσι ώστε οι παρονομαστές να γίνονται οι ίδιοι.

Υπάρχουν πολλοί τρόποι μετατροπής κλασμάτων. Τρία από αυτά συζητούνται στο μάθημα «Μείωση των κλασμάτων σε κοινό παρονομαστή», επομένως δεν θα σταθούμε σε αυτά εδώ. Ας δούμε μερικά παραδείγματα:

Εργο. Βρείτε το νόημα της έκφρασης:

Στην πρώτη περίπτωση, ανάγουμε τα κλάσματα σε έναν κοινό παρονομαστή χρησιμοποιώντας τη μέθοδο «διασταύρωση». Στο δεύτερο θα αναζητήσουμε την ΝΟΕ. Σημειώστε ότι 6 = 2 · 3; 9 = 3 · 3. Οι τελευταίοι παράγοντες σε αυτές τις επεκτάσεις είναι ίσοι και οι πρώτοι είναι σχετικά πρώτοι. Επομένως, LCM(6, 9) = 2 3 3 = 18.

Τι να κάνετε αν ένα κλάσμα έχει ένα ακέραιο μέρος

Μπορώ να σας ευχαριστήσω: διαφορετικοί παρονομαστές σε κλάσματα δεν είναι το μεγαλύτερο κακό. Πολύ περισσότερα σφάλματα συμβαίνουν όταν ολόκληρο το τμήμα επισημαίνεται στα προσθετικά κλάσματα.

Φυσικά, υπάρχουν δικοί αλγόριθμοι πρόσθεσης και αφαίρεσης για τέτοια κλάσματα, αλλά είναι αρκετά περίπλοκοι και απαιτούν μακρά μελέτη. Χρησιμοποιήστε καλύτερα το απλό διάγραμμα παρακάτω:

1. Να μετατρέψετε όλα τα κλάσματα που περιέχουν ένα ακέραιο μέρος σε ακατάλληλα. Λαμβάνουμε κανονικούς όρους (ακόμη και με διαφορετικούς παρονομαστές), οι οποίοι υπολογίζονται σύμφωνα με τους κανόνες που συζητήθηκαν παραπάνω.
2. Στην πραγματικότητα, υπολογίστε το άθροισμα ή τη διαφορά των κλασμάτων που προκύπτουν. Ως αποτέλεσμα, θα βρούμε πρακτικά την απάντηση.
3. Εάν αυτό είναι το μόνο που απαιτείται στο πρόβλημα, εκτελούμε τον αντίστροφο μετασχηματισμό, δηλ. Απαλλαγούμε από ένα ακατάλληλο κλάσμα επισημαίνοντας ολόκληρο το μέρος.

Οι κανόνες για τη μετάβαση σε ακατάλληλα κλάσματα και την επισήμανση ολόκληρου του μέρους περιγράφονται λεπτομερώς στο μάθημα "Τι είναι ένα αριθμητικό κλάσμα". Αν δεν θυμάστε, φροντίστε να το επαναλάβετε. Παραδείγματα:

Εργο. Βρείτε το νόημα της έκφρασης:

Όλα είναι απλά εδώ. Οι παρονομαστές μέσα σε κάθε έκφραση είναι ίσοι, οπότε το μόνο που μένει είναι να μετατρέψουμε όλα τα κλάσματα σε ακατάλληλα και να μετρήσουμε. Εχουμε:

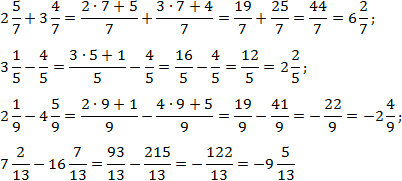
Για να απλοποιήσω τους υπολογισμούς, έχω παραλείψει ορισμένα προφανή βήματα στα τελευταία παραδείγματα.

Μια μικρή σημείωση για τα δύο τελευταία παραδείγματα, όπου αφαιρούνται τα κλάσματα με τονισμένο ακέραιο μέρος. Το μείον πριν από το δεύτερο κλάσμα σημαίνει ότι αφαιρείται ολόκληρο το κλάσμα και όχι μόνο ολόκληρο το μέρος του.

Ξαναδιάβασε αυτή την πρόταση ξανά, δες τα παραδείγματα - και σκέψου το. Αυτό είναι όπου οι αρχάριοι κάνουν έναν τεράστιο αριθμό λαθών. Τους αρέσει να δίνουν τέτοια προβλήματα στις δοκιμές. Θα τα συναντήσετε επίσης αρκετές φορές στα τεστ για αυτό το μάθημα, που θα δημοσιευτούν σύντομα.

Περίληψη: γενικό σχήμα υπολογισμού

Εν κατακλείδι, θα δώσω έναν γενικό αλγόριθμο που θα σας βοηθήσει να βρείτε το άθροισμα ή τη διαφορά δύο ή περισσότερων κλασμάτων:

1. Εάν ένα ή περισσότερα κλάσματα έχουν ένα ακέραιο μέρος, μετατρέψτε αυτά τα κλάσματα σε ακατάλληλα.
2. Φέρτε όλα τα κλάσματα σε έναν κοινό παρονομαστή με κάθε τρόπο που σας βολεύει (εκτός, φυσικά, αν το έκαναν αυτό οι συντάκτες των προβλημάτων).
3. Προσθέστε ή αφαιρέστε τους αριθμούς που προκύπτουν σύμφωνα με τους κανόνες για την πρόσθεση και την αφαίρεση κλασμάτων με όμοιους παρονομαστές.
4. Εάν είναι δυνατόν, συντομεύστε το αποτέλεσμα. Εάν το κλάσμα είναι λανθασμένο, επιλέξτε ολόκληρο το τμήμα.

Θυμηθείτε ότι είναι καλύτερο να επισημάνετε ολόκληρο το μέρος στο τέλος της εργασίας, αμέσως πριν γράψετε την απάντηση.

Ενέργειες με κλάσματα.

Προσοχή!
Υπάρχουν επιπλέον
υλικά στο Ειδικό Τμήμα 555.
Για όσους είναι πολύ "όχι πολύ..."
Και για όσους «πολύ…»)

Λοιπόν, τι είναι τα κλάσματα, τα είδη των κλασμάτων, οι μετασχηματισμοί - θυμηθήκαμε. Πάμε στο κύριο θέμα.

Τι μπορείτε να κάνετε με τα κλάσματα;Ναι, όλα είναι ίδια με τους συνηθισμένους αριθμούς. Προσθήκη, αφαίρεση, πολλαπλασιασμός, διαίρεση.

Όλες αυτές οι ενέργειες με δεκαδικόςΗ εργασία με κλάσματα δεν διαφέρει από την εργασία με ακέραιους αριθμούς. Στην πραγματικότητα, αυτό είναι το καλό με αυτά, δεκαδικά. Το μόνο πράγμα είναι ότι πρέπει να βάλετε σωστά το κόμμα.

Μικτά νούμερα, όπως είπα ήδη, είναι ελάχιστα χρήσιμα για τις περισσότερες ενέργειες. Πρέπει ακόμα να μετατραπούν σε συνηθισμένα κλάσματα.

Αλλά οι ενέργειες με συνηθισμένα κλάσματα θα είναι πιο πονηροί. Και πολύ πιο σημαντικό! Να σας θυμίσω: όλες οι ενέργειες με κλασματικές εκφράσεις με γράμματα, ημίτονο, άγνωστα και ούτω καθεξής και ούτω καθεξής δεν διαφέρουν από τις ενέργειες με συνηθισμένα κλάσματα! Οι πράξεις με συνηθισμένα κλάσματα είναι η βάση για όλη την άλγεβρα. Για αυτόν τον λόγο θα αναλύσουμε όλη αυτή την αριθμητική με μεγάλη λεπτομέρεια εδώ.

Πρόσθεση και αφαίρεση κλασμάτων.

Ο καθένας μπορεί να προσθέσει (αφαιρέσει) κλάσματα με τους ίδιους παρονομαστές (ελπίζω πραγματικά!). Λοιπόν, επιτρέψτε μου να υπενθυμίσω σε όσους είναι εντελώς ξεχασιάρηδες: κατά την πρόσθεση (αφαίρεση), ο παρονομαστής δεν αλλάζει. Οι αριθμητές προστίθενται (αφαιρούνται) για να δώσουν τον αριθμητή του αποτελέσματος. Τύπος:

Με λίγα λόγια, μέσα γενική εικόνα:

Τι γίνεται αν οι παρονομαστές είναι διαφορετικοί; Έπειτα, χρησιμοποιώντας τη βασική ιδιότητα ενός κλάσματος (εδώ πάλι μας βολεύει!), κάνουμε τους παρονομαστές ίδιους! Για παράδειγμα:

Εδώ έπρεπε να κάνουμε το κλάσμα 4/10 από το κλάσμα 2/5. Με αποκλειστικό σκοπό να γίνουν οι παρονομαστές ίδιοι. Επιτρέψτε μου να σημειώσω, για κάθε ενδεχόμενο, ότι τα 2/5 και τα 4/10 είναι το ίδιο κλάσμα! Μόνο τα 2/5 είναι άβολα για εμάς και τα 4/10 είναι πραγματικά εντάξει.

Παρεμπιπτόντως, αυτή είναι η ουσία της επίλυσης οποιωνδήποτε μαθηματικών προβλημάτων. Όταν εμείς από άβολοςκάνουμε εκφράσεις το ίδιο πράγμα, αλλά πιο βολικό για επίλυση.

Ενα άλλο παράδειγμα:

Η κατάσταση είναι παρόμοια. Εδώ κάνουμε 48 από 16. Με απλό πολλαπλασιασμό με το 3. Όλα αυτά είναι ξεκάθαρα. Όμως συναντήσαμε κάτι σαν:

Πώς να είσαι;! Είναι δύσκολο να βγάλεις εννιά στα επτά! Αλλά είμαστε έξυπνοι, ξέρουμε τους κανόνες! Ας μεταμορφωθούμε κάθεκλάσμα έτσι ώστε οι παρονομαστές να είναι ίδιοι. Αυτό ονομάζεται "αναγωγή σε κοινό παρονομαστή":

Ουάου! Πώς ήξερα για το 63; Πολύ απλό! Το 63 είναι ένας αριθμός που διαιρείται με το 7 και το 9 ταυτόχρονα. Ένας τέτοιος αριθμός μπορεί πάντα να ληφθεί πολλαπλασιάζοντας τους παρονομαστές. Αν πολλαπλασιάσουμε έναν αριθμό επί 7, για παράδειγμα, τότε το αποτέλεσμα σίγουρα θα διαιρείται με το 7!

Εάν χρειάζεται να προσθέσετε (αφαιρέσετε) πολλά κλάσματα, δεν χρειάζεται να το κάνετε σε ζευγάρια, βήμα προς βήμα. Απλά πρέπει να βρείτε τον κοινό παρονομαστή σε όλα τα κλάσματα και να μειώσετε κάθε κλάσμα στον ίδιο παρονομαστή. Για παράδειγμα:

Και ποιος θα είναι ο κοινός παρονομαστής; Μπορείτε, φυσικά, να πολλαπλασιάσετε το 2, το 4, το 8 και το 16. Παίρνουμε 1024. Εφιάλτης. Είναι ευκολότερο να υπολογίσουμε ότι ο αριθμός 16 διαιρείται απόλυτα με το 2, το 4 και το 8. Επομένως, από αυτούς τους αριθμούς είναι εύκολο να ληφθεί το 16. Αυτός ο αριθμός θα είναι ο κοινός παρονομαστής. Ας μετατρέψουμε το 1/2 σε 8/16, το 3/4 σε 16/12 και ούτω καθεξής.

Παρεμπιπτόντως, αν πάρετε το 1024 ως κοινό παρονομαστή, όλα θα πάνε καλά, στο τέλος όλα θα μειωθούν. Αλλά δεν θα φτάσουν όλοι σε αυτό το τέλος, λόγω των υπολογισμών...

Συμπληρώστε το παράδειγμα μόνοι σας. Όχι κάποιου είδους λογάριθμος... Θα έπρεπε να είναι 16/29.

Λοιπόν, η πρόσθεση (αφαίρεση) των κλασμάτων είναι σαφής, ελπίζω; Φυσικά, είναι πιο εύκολο να δουλέψετε σε συντομευμένη έκδοση, με επιπλέον πολλαπλασιαστές. Αλλά αυτή την ευχαρίστηση έχουν όσοι εργάστηκαν τίμια στις κατώτερες τάξεις... Και δεν ξέχασαν τίποτα.

Και τώρα θα κάνουμε τις ίδιες ενέργειες, αλλά όχι με κλάσματα, αλλά με κλασματικές εκφράσεις. Νέα γκανιότα θα αποκαλυφθεί εδώ, ναι...

Επομένως, πρέπει να προσθέσουμε δύο κλασματικές εκφράσεις:

Πρέπει να κάνουμε τους παρονομαστές ίδιους. Και μόνο με τη βοήθεια πολλαπλασιασμός! Αυτό υπαγορεύει η κύρια ιδιότητα ενός κλάσματος. Επομένως, δεν μπορώ να προσθέσω ένα στο Χ στο πρώτο κλάσμα στον παρονομαστή. (αυτό θα ήταν ωραίο!). Αλλά αν πολλαπλασιάσετε τους παρονομαστές, βλέπετε, όλα μεγαλώνουν μαζί! Γράφουμε λοιπόν τη γραμμή του κλάσματος, αφήνουμε κενό κενό στην κορυφή, το προσθέτουμε και γράφουμε το γινόμενο των παρονομαστών παρακάτω, για να μην ξεχάσουμε:

Και, φυσικά, δεν πολλαπλασιάζουμε τίποτα στη δεξιά πλευρά, δεν ανοίγουμε την παρένθεση! Και τώρα, κοιτάζοντας τον κοινό παρονομαστή στη δεξιά πλευρά, συνειδητοποιούμε: για να λάβετε τον παρονομαστή x(x+1) στο πρώτο κλάσμα, πρέπει να πολλαπλασιάσετε τον αριθμητή και τον παρονομαστή αυτού του κλάσματος με (x+1) . Και στο δεύτερο κλάσμα - στο x. Αυτό είναι αυτό που παίρνετε:

Σημείωση! Ιδού οι παρενθέσεις! Αυτή είναι η τσουγκράνα που πατάνε πολλοί. Όχι βέβαια παρενθέσεις, αλλά η απουσία τους. Οι παρενθέσεις εμφανίζονται γιατί πολλαπλασιαζόμαστε όλααριθμητής και όλαπαρονομαστής! Και όχι τα μεμονωμένα κομμάτια τους...

Στον αριθμητή της δεξιάς πλευράς γράφουμε το άθροισμα των αριθμητών, όλα είναι όπως στα αριθμητικά κλάσματα, μετά ανοίγουμε τις αγκύλες στον αριθμητή της δεξιάς πλευράς, δηλ. Πολλαπλασιάζουμε τα πάντα και δίνουμε παρόμοια. Δεν χρειάζεται να ανοίξετε τις παρενθέσεις στους παρονομαστές ή να πολλαπλασιάσετε οτιδήποτε! Γενικά, σε παρονομαστές (οποιονδήποτε) το προϊόν είναι πάντα πιο ευχάριστο! Παίρνουμε:

Λοιπόν πήραμε την απάντηση. Η διαδικασία φαίνεται μακρά και δύσκολη, αλλά εξαρτάται από την πρακτική. Μόλις λύσετε τα παραδείγματα, συνηθίσετε, όλα θα γίνουν απλά. Όσοι έχουν κατακτήσει τα κλάσματα σε εύθετο χρόνο κάνουν όλες αυτές τις πράξεις με το ένα αριστερό χέρι, αυτόματα!

Και μια ακόμη σημείωση. Πολλοί αντιμετωπίζουν έξυπνα τα κλάσματα, αλλά κολλάνε σε παραδείγματα ολόκληροςαριθμοί. Μου αρέσει: 2 + 1/2 + 3/4= ? Πού να στερεώσω το δικομμένο; Δεν χρειάζεται να το στερεώσετε πουθενά, πρέπει να κάνετε ένα κλάσμα από τα δύο. Δεν είναι εύκολο, αλλά πολύ απλό! 2=2/1. Σαν αυτό. Οποιοσδήποτε ακέραιος αριθμός μπορεί να γραφτεί ως κλάσμα. Ο αριθμητής είναι ο ίδιος ο αριθμός, ο παρονομαστής είναι ένας. Το 7 είναι 7/1, το 3 είναι 3/1 και ούτω καθεξής. Το ίδιο συμβαίνει και με τα γράμματα. (a+b) = (a+b)/1, x=x/1, κ.λπ. Και μετά δουλεύουμε με αυτά τα κλάσματα σύμφωνα με όλους τους κανόνες.

Λοιπόν, οι γνώσεις της πρόσθεσης και της αφαίρεσης των κλασμάτων ανανεώθηκαν. Η μετατροπή κλασμάτων από έναν τύπο σε άλλο επαναλήφθηκε. Μπορείτε επίσης να κάνετε έλεγχο. Να το τακτοποιήσουμε λίγο;)

Υπολογίζω:

Απαντήσεις (σε αταξία):

71/20; 3/5; 17/12; -5/4; 11/6

Πολλαπλασιασμός/διαίρεση κλασμάτων - στο επόμενο μάθημα. Υπάρχουν επίσης εργασίες για όλες τις πράξεις με κλάσματα.

Αν σας αρέσει αυτό το site...

Παρεμπιπτόντως, έχω μερικές ακόμη ενδιαφέρουσες τοποθεσίες για εσάς.)

Μπορείτε να εξασκηθείτε στην επίλυση παραδειγμάτων και να μάθετε το επίπεδό σας. Δοκιμή με άμεση επαλήθευση. Ας μάθουμε - με ενδιαφέρον!)

Μπορείτε να εξοικειωθείτε με συναρτήσεις και παραγώγους.

Μπορείτε να εκτελέσετε διάφορες λειτουργίες με κλάσματα, για παράδειγμα, να προσθέσετε κλάσματα. Η προσθήκη κλασμάτων μπορεί να χωριστεί σε διάφορους τύπους. Κάθε τύπος πρόσθεσης κλασμάτων έχει τους δικούς του κανόνες και αλγόριθμο ενεργειών. Ας δούμε αναλυτικά κάθε τύπο προσθήκης.

Προσθήκη κλασμάτων με όμοιους παρονομαστές.

Ας δούμε ένα παράδειγμα του τρόπου προσθήκης κλασμάτων με κοινό παρονομαστή.

Οι τουρίστες έκαναν πεζοπορία από το σημείο Α στο σημείο Ε. Την πρώτη μέρα περπάτησαν από το σημείο Α στο Β ή \(\frac(1)(5)\) ολόκληρου του μονοπατιού. Τη δεύτερη μέρα περπάτησαν από το σημείο Β στο Δ ή \(\frac(2)(5)\) όλη τη διαδρομή. Πόσο μακριά διένυσαν από την αρχή του ταξιδιού μέχρι το σημείο Δ;

Για να βρείτε την απόσταση από το σημείο Α στο σημείο Δ, πρέπει να προσθέσετε τα κλάσματα \(\frac(1)(5) + \frac(2)(5)\).

Η προσθήκη κλασμάτων με παρονομαστές παρόμοιους σημαίνει ότι πρέπει να προσθέσετε τους αριθμητές αυτών των κλασμάτων, αλλά ο παρονομαστής θα παραμείνει ο ίδιος.

\(\frac(1)(5) + \frac(2)(5) = \frac(1 + 2)(5) = \frac(3)(5)\)

Σε κυριολεκτική μορφή, το άθροισμα των κλασμάτων με τους ίδιους παρονομαστές θα μοιάζει με αυτό:

\(\bf \frac(a)(c) + \frac(b)(c) = \frac(a + b)(c)\)

Απάντηση: οι τουρίστες περπάτησαν \(\frac(3)(5)\) όλη τη διαδρομή.

Προσθήκη κλασμάτων με διαφορετικούς παρονομαστές.

Ας δούμε ένα παράδειγμα:

Πρέπει να προσθέσετε δύο κλάσματα \(\frac(3)(4)\) και \(\frac(2)(7)\).

Για να προσθέσετε κλάσματα με διαφορετικούς παρονομαστές, πρέπει πρώτα να βρείτε, και μετά χρησιμοποιήστε τον κανόνα για την προσθήκη κλασμάτων με παρονομαστές όμοιους.

Για τους παρονομαστές 4 και 7, ο κοινός παρονομαστής θα είναι ο αριθμός 28. Το πρώτο κλάσμα \(\frac(3)(4)\) πρέπει να πολλαπλασιαστεί επί 7. Το δεύτερο κλάσμα \(\frac(2)(7)\ ) πρέπει να πολλαπλασιαστεί επί 4.

\(\frac(3)(4) + \frac(2)(7) = \frac(3 \times \color(red) (7) + 2 \times \color(κόκκινο) (4))(4 \ φορές \χρώμα(κόκκινο) (7)) = \frac(21 + 8)(28) = \frac(29)(28) = 1\frac(1)(28)\)

Σε κυριολεκτική μορφή παίρνουμε τον ακόλουθο τύπο:

\(\bf \frac(a)(b) + \frac(c)(d) = \frac(a \times d + c \times b)(b \φορές d)\)

Προσθήκη μικτών αριθμών ή μικτών κλασμάτων.

Η πρόσθεση γίνεται σύμφωνα με το νόμο της πρόσθεσης.

Για μικτά κλάσματα προσθέτουμε τα ολόκληρα με τα ολόκληρα μέρη και τα κλασματικά με τα κλάσματα.

Αν τα κλασματικά μέρη μικτών αριθμών έχουν ίδιοι παρονομαστές, τότε προσθέτουμε τους αριθμητές, αλλά ο παρονομαστής παραμένει ίδιος.

Ας προσθέσουμε τους μεικτούς αριθμούς \(3\frac(6)(11)\) και \(1\frac(3)(11)\).

\(3\frac(6)(11) + 1\frac(3)(11) = (\color(κόκκινο) (3) + \color(μπλε) (\frac(6)(11))) + ( \color(red) (1) + \color(blue) (\frac(3)(11))) = (\color(red) (3) + \color(red) (1)) + (\color( μπλε) (\frac(6)(11)) + \color(blue) (\frac(3)(11))) = \color(red)(4) + (\color(blue) (\frac(6) + 3)(11)) = \color(κόκκινο)(4) + \color(μπλε) (\frac(9)(11)) = \color(κόκκινο)(4) \color(μπλε) (\frac (9)(11))\)

Αν τα κλασματικά μέρη των μικτών αριθμών έχουν διαφορετικούς παρονομαστές, τότε βρίσκουμε τον κοινό παρονομαστή.

Ας εκτελέσουμε την πρόσθεση μικτών αριθμών \(7\frac(1)(8)\) και \(2\frac(1)(6)\).

Ο παρονομαστής είναι διαφορετικός, επομένως πρέπει να βρούμε τον κοινό παρονομαστή, είναι ίσος με 24. Πολλαπλασιάστε το πρώτο κλάσμα \(7\frac(1)(8)\) με έναν επιπλέον παράγοντα 3, και το δεύτερο κλάσμα \( 2\frac(1)(6)\) επί 4.

\(7\frac(1)(8) + 2\frac(1)(6) = 7\frac(1 \times \color(red) (3))(8 \times \color(κόκκινο) (3) ) = 2\frac(1\times \color(κόκκινο) (4))(6\times \color(κόκκινο) (4)) =7\frac(3)(24) + 2\frac(4)(24 ) = 9\frac(7)(24)\)

Σχετικές ερωτήσεις:
Πώς να προσθέσετε κλάσματα;
Απάντηση: πρώτα πρέπει να αποφασίσετε ποιος τύπος έκφρασης είναι: τα κλάσματα έχουν τους ίδιους παρονομαστές, διαφορετικούς παρονομαστές ή μικτά κλάσματα. Ανάλογα με το είδος της έκφρασης προχωράμε στον αλγόριθμο επίλυσης.

Πώς να λύσετε κλάσματα με διαφορετικούς παρονομαστές;
Απάντηση: πρέπει να βρείτε τον κοινό παρονομαστή και στη συνέχεια να ακολουθήσετε τον κανόνα της πρόσθεσης κλασμάτων με τους ίδιους παρονομαστές.

Πώς να λύσετε μικτά κλάσματα;
Απάντηση: προσθέτουμε ακέραια μέρη με ακέραιους και κλασματικά με κλάσματα.

Παράδειγμα #1:
Μπορεί το άθροισμα δύο να οδηγήσει σε ένα σωστό κλάσμα; Ακατάλληλο κλάσμα; Δώσε παραδείγματα.

\(\frac(2)(7) + \frac(3)(7) = \frac(2 + 3)(7) = \frac(5)(7)\)

Το κλάσμα \(\frac(5)(7)\) είναι ένα σωστό κλάσμα, είναι το αποτέλεσμα του αθροίσματος δύο κατάλληλων κλασμάτων \(\frac(2)(7)\) και \(\frac(3) (7)\).

\(\frac(2)(5) + \frac(8)(9) = \frac(2 \times 9 + 8 \times 5)(5 \times 9) =\frac(18 + 40)(45) = \frac(58)(45)\)

Το κλάσμα \(\frac(58)(45)\) είναι ένα ακατάλληλο κλάσμα, είναι το αποτέλεσμα του αθροίσματος των κατάλληλων κλασμάτων \(\frac(2)(5)\) και \(\frac(8) (9)\).

Απάντηση: Η απάντηση και στις δύο ερωτήσεις είναι ναι.

Παράδειγμα #2:
Προσθέστε τα κλάσματα: α) \(\frac(3)(11) + \frac(5)(11)\) β) \(\frac(1)(3) + \frac(2)(9)\) .

α) \(\frac(3)(11) + \frac(5)(11) = \frac(3 + 5)(11) = \frac(8)(11)\)

β) \(\frac(1)(3) + \frac(2)(9) = \frac(1 \times \color(red) (3))(3 \times \color(κόκκινο) (3)) + \frac(2)(9) = \frac(3)(9) + \frac(2)(9) = \frac(5)(9)\)

Παράδειγμα #3:
Σημειώστε το μικτό κλάσμαως άθροισμα φυσικός αριθμόςκαι σωστό κλάσμα: α) \(1\frac(9)(47)\) β) \(5\frac(1)(3)\)

α) \(1\frac(9)(47) = 1 + \frac(9)(47)\)

β) \(5\frac(1)(3) = 5 + \frac(1)(3)\)

Παράδειγμα #4:
Υπολογίστε το άθροισμα: α) \(8\frac(5)(7) + 2\frac(1)(7)\) β) \(2\frac(9)(13) + \frac(2)(13 ) \) γ) \(7\frac(2)(5) + 3\frac(4)(15)\)

α) \(8\frac(5)(7) + 2\frac(1)(7) = (8 + 2) + (\frac(5)(7) + \frac(1)(7)) = 10 + \frac(6)(7) = 10\frac(6)(7)\)

β) \(2\frac(9)(13) + \frac(2)(13) = 2 + (\frac(9)(13) + \frac(2)(13)) = 2\frac(11 )(13) \)

γ) \(7\frac(2)(5) + 3\frac(4)(15) = 7\frac(2\ φορές 3)(5\ φορές 3) + 3\frac(4)(15) = 7\frac(6)(15) + 3\frac(4)(15) = (7 + 3)+(\frac(6)(15) + \frac(4)(15)) = 10 + \frac (10)(15) = 10\frac(10)(15) = 10\frac(2)(3)\)

Εργασία #1:
Το μεσημεριανό γεύμα φάγαμε \(\frac(8)(11)\) από το κέικ, και το βράδυ στο δείπνο φάγαμε \(\frac(3)(11)\). Πιστεύετε ότι η τούρτα φαγώθηκε εντελώς ή όχι;

Λύση:
Ο παρονομαστής του κλάσματος είναι 11, δείχνει σε πόσα μέρη χωρίστηκε το κέικ. Στο μεσημεριανό φάγαμε 8 κομμάτια κέικ από τα 11. Στο βραδινό φάγαμε 3 κομμάτια κέικ από τα 11. Ας προσθέσουμε 8 + 3 = 11, φάγαμε κομμάτια κέικ από τα 11, δηλαδή ολόκληρο το κέικ.

\(\frac(8)(11) + \frac(3)(11) = \frac(11)(11) = 1\)

Απάντηση: φαγώθηκε ολόκληρη η τούρτα.

Τον πέμπτο αιώνα π.Χ., ο αρχαίος Έλληνας φιλόσοφος Ζήνων από την Ελαία διατύπωσε τις περίφημες απορίας του, η πιο γνωστή από τις οποίες είναι η απορία «Αχιλλέας και η Χελώνα». Να πώς ακούγεται:

Ας πούμε ότι ο Αχιλλέας τρέχει δέκα φορές πιο γρήγορα από τη χελώνα και είναι χίλια βήματα πίσω της. Κατά τη διάρκεια του χρόνου που χρειάζεται ο Αχιλλέας για να τρέξει αυτή την απόσταση, η χελώνα θα σέρνεται εκατό βήματα προς την ίδια κατεύθυνση. Όταν ο Αχιλλέας τρέχει εκατό βήματα, η χελώνα σέρνεται άλλα δέκα βήματα, και ούτω καθεξής. Η διαδικασία θα συνεχιστεί επ’ άπειρον, ο Αχιλλέας δεν θα προλάβει ποτέ τη χελώνα.

Αυτό το σκεπτικό έγινε ένα λογικό σοκ για όλες τις επόμενες γενιές. Αριστοτέλης, Διογένης, Καντ, Χέγκελ, Χίλμπερτ... Όλοι θεωρούσαν την απορία του Ζήνωνα με τον ένα ή τον άλλο τρόπο. Το σοκ ήταν τόσο δυνατό που " ...οι συζητήσεις συνεχίζονται μέχρι σήμερα· η επιστημονική κοινότητα δεν έχει καταφέρει ακόμη να καταλήξει σε κοινή γνώμη για την ουσία των παραδόξων... συμμετείχαν στη μελέτη του θέματος μαθηματική ανάλυση, θεωρία συνόλων, νέες φυσικές και φιλοσοφικές προσεγγίσεις. κανένα από αυτά δεν έγινε μια γενικά αποδεκτή λύση στο πρόβλημα..."[Wikipedia, "Zeno's Aporia". Όλοι καταλαβαίνουν ότι τους κοροϊδεύουν, αλλά κανείς δεν καταλαβαίνει σε τι συνίσταται η εξαπάτηση.

Από μαθηματική άποψη, ο Ζήνων στην απορία του έδειξε ξεκάθαρα τη μετάβαση από την ποσότητα στο . Αυτή η μετάβαση συνεπάγεται εφαρμογή αντί για μόνιμες. Από όσο καταλαβαίνω, η μαθηματική συσκευή για τη χρήση μεταβλητών μονάδων μέτρησης είτε δεν έχει ακόμη αναπτυχθεί, είτε δεν έχει εφαρμοστεί στην απορία του Ζήνωνα. Η εφαρμογή της συνηθισμένης λογικής μας οδηγεί σε μια παγίδα. Εμείς, λόγω της αδράνειας της σκέψης, εφαρμόζουμε σταθερές μονάδες χρόνου στην αμοιβαία τιμή. Από φυσική άποψη, αυτό μοιάζει να επιβραδύνεται ο χρόνος μέχρι να σταματήσει εντελώς τη στιγμή που ο Αχιλλέας προλαβαίνει τη χελώνα. Αν ο χρόνος σταματήσει, ο Αχιλλέας δεν μπορεί πλέον να ξεπεράσει τη χελώνα.

Αν γυρίσουμε τη συνηθισμένη μας λογική, όλα μπαίνουν στη θέση τους. Ο Αχιλλέας τρέχει με σταθερή ταχύτητα. Κάθε επόμενο τμήμα της διαδρομής του είναι δέκα φορές μικρότερο από το προηγούμενο. Αντίστοιχα, ο χρόνος που δαπανάται για την αντιμετώπισή του είναι δέκα φορές μικρότερος από τον προηγούμενο. Εάν εφαρμόσουμε την έννοια του «άπειρου» σε αυτήν την κατάσταση, τότε θα ήταν σωστό να πούμε «Ο Αχιλλέας θα προλάβει τη χελώνα απείρως γρήγορα».

Πώς να αποφύγετε αυτή τη λογική παγίδα; Παραμείνετε σε σταθερές μονάδες χρόνου και μην μεταβείτε σε αντίστροφες μονάδες. Στη γλώσσα του Ζήνωνα μοιάζει με αυτό:

Στον χρόνο που χρειάζεται ο Αχιλλέας για να τρέξει χίλια βήματα, η χελώνα θα σέρνεται εκατό βήματα προς την ίδια κατεύθυνση. Στο επόμενο χρονικό διάστημα ίσο με το πρώτο, ο Αχιλλέας θα τρέξει άλλα χίλια βήματα και η χελώνα θα σέρνεται εκατό βήματα. Τώρα ο Αχιλλέας είναι οκτακόσια βήματα μπροστά από τη χελώνα.

Αυτή η προσέγγιση περιγράφει επαρκώς την πραγματικότητα χωρίς λογικά παράδοξα. Αλλά αυτό δεν είναι μια πλήρης λύση στο πρόβλημα. Η δήλωση του Αϊνστάιν για το ακαταμάχητο της ταχύτητας του φωτός μοιάζει πολύ με την απορία του Ζήνωνα «Ο Αχιλλέας και η Χελώνα». Πρέπει ακόμα να μελετήσουμε, να ξανασκεφτούμε και να λύσουμε αυτό το πρόβλημα. Και η λύση πρέπει να αναζητηθεί όχι σε απείρως μεγάλους αριθμούς, αλλά σε μονάδες μέτρησης.

Μια άλλη ενδιαφέρουσα απορία του Ζήνωνα λέει για ένα ιπτάμενο βέλος:

Ένα ιπτάμενο βέλος είναι ακίνητο, αφού σε κάθε στιγμή του χρόνου είναι σε ηρεμία, και αφού είναι σε ηρεμία σε κάθε στιγμή του χρόνου, είναι πάντα σε ηρεμία.

Σε αυτήν την απορία, το λογικό παράδοξο ξεπερνιέται πολύ απλά - αρκεί να διευκρινίσουμε ότι σε κάθε στιγμή ένα ιπτάμενο βέλος βρίσκεται σε ηρεμία σε διαφορετικά σημεία του χώρου, που στην πραγματικότητα είναι κίνηση. Εδώ πρέπει να σημειωθεί ένα άλλο σημείο. Από μια φωτογραφία ενός αυτοκινήτου στο δρόμο είναι αδύνατο να προσδιοριστεί ούτε το γεγονός της κίνησής του ούτε η απόσταση από αυτό. Για να προσδιορίσετε αν ένα αυτοκίνητο κινείται, χρειάζεστε δύο φωτογραφίες που τραβήχτηκαν από το ίδιο σημείο σε διαφορετικά χρονικά σημεία, αλλά δεν μπορείτε να προσδιορίσετε την απόσταση από αυτές. Για να προσδιορίσετε την απόσταση από ένα αυτοκίνητο, χρειάζεστε δύο φωτογραφίες από διαφορετικά σημεία του χώρου σε μια χρονική στιγμή, αλλά από αυτές δεν μπορείτε να προσδιορίσετε το γεγονός της κίνησης (φυσικά, χρειάζεστε επιπλέον δεδομένα για υπολογισμούς, η τριγωνομετρία θα σας βοηθήσει ). Αυτό που θέλω να επισημάνω Ιδιαίτερη προσοχή, είναι ότι δύο σημεία στο χρόνο και δύο σημεία στο χώρο είναι διαφορετικά πράγματα που δεν πρέπει να συγχέονται, γιατί παρέχουν διαφορετικές ευκαιρίες για έρευνα.

Τετάρτη 4 Ιουλίου 2018

Οι διαφορές μεταξύ συνόλου και πολλαπλών συνόλων περιγράφονται πολύ καλά στη Wikipedia. Ας δούμε.

Όπως μπορείτε να δείτε, "δεν μπορούν να υπάρχουν δύο πανομοιότυπα στοιχεία σε ένα σύνολο", αλλά εάν υπάρχουν πανομοιότυπα στοιχεία σε ένα σύνολο, ένα τέτοιο σύνολο ονομάζεται "πολυσύνολο". Τα λογικά όντα δεν θα καταλάβουν ποτέ μια τέτοια παράλογη λογική. Αυτό είναι το επίπεδο των παπαγάλων που μιλάνε και των εκπαιδευμένων πιθήκων, που δεν έχουν νοημοσύνη από τη λέξη «εντελώς». Οι μαθηματικοί λειτουργούν ως απλοί εκπαιδευτές, κηρύττοντας μας τις παράλογες ιδέες τους.

Μια φορά κι έναν καιρό, οι μηχανικοί που κατασκεύασαν τη γέφυρα βρίσκονταν σε μια βάρκα κάτω από τη γέφυρα ενώ δοκίμαζαν τη γέφυρα. Αν η γέφυρα κατέρρεε, ο μέτριος μηχανικός πέθαινε κάτω από τα ερείπια του δημιουργήματός του. Αν η γέφυρα μπορούσε να αντέξει το φορτίο, ο ταλαντούχος μηχανικός κατασκεύασε άλλες γέφυρες.

Ανεξάρτητα από το πόσο κρύβονται οι μαθηματικοί πίσω από τη φράση «να με νου, είμαι στο σπίτι», ή μάλλον, «τα μαθηματικά μελετούν αφηρημένες έννοιες», υπάρχει ένας ομφάλιος λώρος που τις συνδέει άρρηκτα με την πραγματικότητα. Αυτός ο ομφάλιος λώρος είναι χρήματα. Εφαρμόσιμος μαθηματική θεωρίασετ στους ίδιους τους μαθηματικούς.

Σπουδάσαμε πολύ καλά μαθηματικά και τώρα καθόμαστε στο ταμείο και βγάζουμε μισθούς. Έρχεται λοιπόν σε εμάς ένας μαθηματικός για τα λεφτά του. Του μετράμε όλο το ποσό και το απλώνουμε στο τραπέζι μας σε διαφορετικούς σωρούς, στους οποίους βάζουμε λογαριασμούς της ίδιας ονομαστικής αξίας. Στη συνέχεια, παίρνουμε έναν λογαριασμό από κάθε σωρό και δίνουμε στον μαθηματικό το «μαθηματικό σύνολο του μισθού» του. Ας εξηγήσουμε στον μαθηματικό ότι θα λάβει τους υπόλοιπους λογαριασμούς μόνο όταν αποδείξει ότι ένα σύνολο χωρίς πανομοιότυπα στοιχεία δεν είναι ίσο με ένα σύνολο με πανομοιότυπα στοιχεία. Εδώ αρχίζει η διασκέδαση.

Πρώτα απ 'όλα, θα λειτουργήσει η λογική των βουλευτών: "Αυτό μπορεί να εφαρμοστεί σε άλλους, αλλά όχι σε μένα!" Τότε θα αρχίσουν να μας καθησυχάζουν ότι τα χαρτονομίσματα της ίδιας ονομαστικής αξίας έχουν διαφορετικούς αριθμούς λογαριασμών, πράγμα που σημαίνει ότι δεν μπορούν να θεωρηθούν τα ίδια στοιχεία. Εντάξει, ας μετρήσουμε τους μισθούς σε νομίσματα - δεν υπάρχουν αριθμοί στα νομίσματα. Εδώ ο μαθηματικός θα αρχίσει να θυμάται μανιωδώς τη φυσική: σε διαφορετικά νομίσματα υπάρχει διαφορετικές ποσότητεςβρωμιά, κρυσταλλική δομή και ατομική διάταξη κάθε νομίσματος είναι μοναδική...

Και τώρα έχω τα περισσότερα ενδιαφέρον Ρωτήστε: πού βρίσκεται η γραμμή πέρα ​​από την οποία τα στοιχεία ενός πολυσυνόλου μετατρέπονται σε στοιχεία ενός συνόλου και αντίστροφα; Δεν υπάρχει τέτοια γραμμή - όλα αποφασίζονται από σαμάνους, η επιστήμη δεν είναι καν κοντά στο να ψεύδεται εδώ.

Κοιτάξτε εδώ. Επιλέγουμε γήπεδα ποδοσφαίρου με τον ίδιο χώρο γηπέδου. Οι περιοχές των πεδίων είναι οι ίδιες - που σημαίνει ότι έχουμε ένα πολυσύνολο. Αλλά αν δούμε τα ονόματα των ίδιων γηπέδων, παίρνουμε πολλά, γιατί τα ονόματα είναι διαφορετικά. Όπως μπορείτε να δείτε, το ίδιο σύνολο στοιχείων είναι και σύνολο και πολυσύνολο. Ποιο είναι σωστό? Και εδώ ο μαθηματικός-σαμάνος-αιχμηρός βγάζει έναν άσσο ατού από το μανίκι του και αρχίζει να μας λέει είτε για σετ είτε για πολυσύνολο. Σε κάθε περίπτωση, θα μας πείσει ότι έχει δίκιο.

Για να κατανοήσουμε πώς λειτουργούν οι σύγχρονοι σαμάνοι με τη θεωρία συνόλων, συνδέοντάς την με την πραγματικότητα, αρκεί να απαντήσουμε σε μια ερώτηση: πώς διαφέρουν τα στοιχεία ενός συνόλου από τα στοιχεία ενός άλλου συνόλου; Θα σας δείξω, χωρίς κανένα «νοητό ως μη ενιαίο σύνολο» ή «μη νοητό ως ενιαίο σύνολο».

Κυριακή 18 Μαρτίου 2018

Το άθροισμα των ψηφίων ενός αριθμού είναι ένας χορός σαμάνων με ντέφι, που δεν έχει καμία σχέση με τα μαθηματικά. Ναι, στα μαθήματα των μαθηματικών διδασκόμαστε να βρίσκουμε το άθροισμα των ψηφίων ενός αριθμού και να το χρησιμοποιούμε, αλλά γι' αυτό είναι σαμάνοι, για να μάθουν στους απογόνους τους τις δεξιότητες και τη σοφία τους, διαφορετικά οι σαμάνοι απλά θα πεθάνουν.

Χρειάζεστε αποδείξεις; Ανοίξτε τη Wikipedia και προσπαθήστε να βρείτε τη σελίδα "Άθροισμα ψηφίων ενός αριθμού". Αυτή δεν υπάρχει. Δεν υπάρχει τύπος στα μαθηματικά που να μπορεί να χρησιμοποιηθεί για να βρεθεί το άθροισμα των ψηφίων οποιουδήποτε αριθμού. Άλλωστε οι αριθμοί είναι γραφικά σύμβολα, με τη βοήθεια του οποίου γράφουμε αριθμούς και στη γλώσσα των μαθηματικών η εργασία ακούγεται ως εξής: «Βρείτε το άθροισμα των γραφικών συμβόλων που αντιπροσωπεύουν οποιονδήποτε αριθμό». Οι μαθηματικοί δεν μπορούν να λύσουν αυτό το πρόβλημα, αλλά οι σαμάνοι μπορούν να το κάνουν εύκολα.

Ας μάθουμε τι και πώς κάνουμε για να βρούμε το άθροισμα των ψηφίων ενός δεδομένου αριθμού. Και λοιπόν, ας έχουμε τον αριθμό 12345. Τι πρέπει να κάνουμε για να βρούμε το άθροισμα των ψηφίων αυτού του αριθμού; Ας εξετάσουμε όλα τα βήματα με τη σειρά.

1. Σημειώστε τον αριθμό σε ένα κομμάτι χαρτί. Τι καναμε? Μετατρέψαμε τον αριθμό σε σύμβολο γραφικού αριθμού. Δεν πρόκειται για μαθηματική πράξη.

2. Κόβουμε μια εικόνα που προκύπτει σε πολλές εικόνες που περιέχουν μεμονωμένους αριθμούς. Η κοπή μιας εικόνας δεν είναι μαθηματική πράξη.

3. Μετατρέψτε μεμονωμένα γραφικά σύμβολα σε αριθμούς. Δεν πρόκειται για μαθηματική πράξη.

4. Προσθέστε τους αριθμούς που προκύπτουν. Τώρα αυτό είναι μαθηματικά.

Το άθροισμα των ψηφίων του αριθμού 12345 είναι 15. Αυτά είναι τα «μαθήματα κοπής και ραπτικής» που διδάσκονται από σαμάνους που χρησιμοποιούν οι μαθηματικοί. Αλλά δεν είναι μόνο αυτό.

Από μαθηματική άποψη, δεν έχει σημασία σε ποιο σύστημα αριθμών γράφουμε έναν αριθμό. Έτσι, σε διαφορετικά συστήματα αριθμών το άθροισμα των ψηφίων του ίδιου αριθμού θα είναι διαφορετικό. Στα μαθηματικά, το σύστημα αριθμών υποδεικνύεται ως δείκτης στα δεξιά του αριθμού. ΜΕ ένας μεγάλος αριθμός 12345 Δεν θέλω να κοροϊδέψω το κεφάλι μου, ας δούμε τον αριθμό 26 από το άρθρο για το . Ας γράψουμε αυτόν τον αριθμό σε δυαδικά, οκταδικά, δεκαδικά και δεκαεξαδικά συστήματα αριθμών. Δεν θα εξετάσουμε κάθε βήμα κάτω από ένα μικροσκόπιο· το έχουμε ήδη κάνει. Ας δούμε το αποτέλεσμα.

Όπως μπορείτε να δείτε, σε διαφορετικά συστήματα αριθμών το άθροισμα των ψηφίων του ίδιου αριθμού είναι διαφορετικό. Αυτό το αποτέλεσμα δεν έχει καμία σχέση με τα μαθηματικά. Είναι το ίδιο σαν να προσδιορίζατε το εμβαδόν ενός ορθογωνίου σε μέτρα και εκατοστά, θα είχατε εντελώς διαφορετικά αποτελέσματα.

Το μηδέν φαίνεται το ίδιο σε όλα τα συστήματα αριθμών και δεν έχει άθροισμα ψηφίων. Αυτό είναι ένα άλλο επιχείρημα υπέρ του γεγονότος ότι. Ερώτηση για μαθηματικούς: πώς ορίζεται κάτι που δεν είναι αριθμός στα μαθηματικά; Τι, για τους μαθηματικούς δεν υπάρχει τίποτα εκτός από αριθμούς; Μπορώ να το επιτρέψω για σαμάνους, αλλά όχι για επιστήμονες. Η πραγματικότητα δεν αφορά μόνο αριθμούς.

Το αποτέλεσμα που προκύπτει θα πρέπει να θεωρείται ως απόδειξη ότι τα συστήματα αριθμών είναι μονάδες μέτρησης για αριθμούς. Εξάλλου, δεν μπορούμε να συγκρίνουμε αριθμούς με διαφορετικές μονάδες μέτρησης. Αν οι ίδιες ενέργειες με διαφορετικές μονάδες μέτρησης της ίδιας ποσότητας οδηγούν σε διαφορετικά αποτελέσματααφού τα συγκρίνεις, σημαίνει ότι δεν έχει καμία σχέση με τα μαθηματικά.

Τι είναι τα πραγματικά μαθηματικά; Αυτό συμβαίνει όταν το αποτέλεσμα μιας μαθηματικής πράξης δεν εξαρτάται από το μέγεθος του αριθμού, τη μονάδα μέτρησης που χρησιμοποιείται και από το ποιος εκτελεί αυτήν την ενέργεια.

Σημάδι στην πόρτα Ανοίγει την πόρτα και λέει:

Ω! Αυτή δεν είναι η γυναικεία τουαλέτα;
- Νέα γυναίκα! Αυτό είναι ένα εργαστήριο για τη μελέτη της άφιλης αγιότητας των ψυχών κατά την ανάληψή τους στον ουρανό! Φωτοστέφανο στην κορυφή και βέλος επάνω. Τι άλλη τουαλέτα;

Θηλυκό... Το φωτοστέφανο από πάνω και το βέλος κάτω είναι αρσενικό.

Εάν ένα τέτοιο έργο τέχνης σχεδιασμού αναβοσβήνει μπροστά στα μάτια σας πολλές φορές την ημέρα,

Τότε δεν είναι περίεργο που βρίσκετε ξαφνικά ένα περίεργο εικονίδιο στο αυτοκίνητό σας:

Προσωπικά, προσπαθώ να δω μείον τέσσερις μοίρες σε ένα άτομο που σκάει (μία εικόνα) (μια σύνθεση πολλών εικόνων: ένα σύμβολο μείον, ο αριθμός τέσσερα, ένας προσδιορισμός μοιρών). Και δεν νομίζω ότι αυτό το κορίτσι είναι ανόητο που δεν ξέρει φυσική. Απλώς έχει ένα ισχυρό στερεότυπο για την αντίληψη γραφικών εικόνων. Και αυτό μας διδάσκουν συνέχεια οι μαθηματικοί. Εδώ είναι ένα παράδειγμα.

Το 1Α δεν είναι «μείον τέσσερις μοίρες» ή «ένα α». Αυτό είναι το "pooping man" ή ο αριθμός "είκοσι έξι" σε δεκαεξαδικό συμβολισμό. Όσοι εργάζονται συνεχώς σε αυτό το σύστημα αριθμών αντιλαμβάνονται αυτόματα έναν αριθμό και ένα γράμμα ως ένα γραφικό σύμβολο.